Билет 22 Неопределенный интеграл. Его свойства.

Определение 1: Функция F называется первообразной функции f на интервале (a,b), если функция f непрерывна на интервале (a,b), и для всех x из этого интервала выполняется равенство: F΄(x)=f(x).

Замечание: Вместо (a,b) можно рассматривать [a,b], (a,b] и [a,b), но нужно будет говорить про односторонние производные: =f(a), и=f(b).

Пример

.

на промежутке (-∞,0) и на (0,+∞).

Теорема:(О множестве всех первообразных).

Пусть F(x) является первообразной функции f(x) на на промежутке I, тогда функции вида F(x)+C и только они являются первообразными функции f(x), где C – произвольная константа.

Доказательство:

Пусть функция F(x) – первообразная функции f(x), тогда F΄(x)=f(x) и (F(x)+C)΄=f(x). Пусть функции F и G – первообразные функции f(x) на промежутке I (нужно доказать, что они отличаются на константу). Тогда (F-G)΄=0F-G=C (по теореме о функции, имеющей нулевую производную).

Теорема доказана.

Определение 2: Множество всех первообразных функции f(x) на промежутке I называется неопределенным интегралом и обозначается. При этом если функция F(x) – первообразная функции f(x), то.

Пример:

.

Свойства первообразных и неопределенного интеграла.

1. Пусть функция f(x) имеет первообразную F(x) на промежутке I и функция g(x) имеет первообразную G(x) на промежутке I, тогда функция f(x)±g(x) будет иметь первообразную F(x)±G(x) на промежутке I. Для интегралов:.

Замечание: Обратное неверно! Из существования интеграла не следует существование интегралови.

Первообразной функции k·f(x) является функция k·F(x). Для интегралов:.

2. Первообразной производной функции f΄(x) является сама функция f(x). Для интегралов: .

3. (по определению).

Билет 23

Метод внесения од знак дифференциала, метод подстановки.

Билет 24

Интегрирование по частям.

Билет 25

Интегрирование рациональных дробей.

Билет 26

Интегрирование иррациональных функций.

Билет 27

Интегрирование тригонометрических функций.

Билет 28

Интегральная сумма, ее предел. Определение определенного интеграла.

Билет 29

Необходимое условие интегрируемости.

Билет 30

Суммы Дарбу, их свойства.

Билет 31

Необходимое и достаточное условия интегрируемости функции.

Билет 32

Достаточные условия интегрируемости функции.

Интегрируемость по Риману непрерывной функции.

Теорема 1:

Если функция 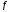непрерывна на, то она интегрируема на.

Доказательство:

Пустьнепрерывна на; тогда для разбиения R, у которого частичные отрезки, имеет место ().

где есть модуль непрерывностина.

Поэтому

.

Но, как мы знаем, для непрерывной на замкнутом конечном отрезке функции, поэтому для любогоможно указать такое, что.

В силу основной теоремы интегрална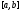существует.

Теорема доказана.

Интегрируемость по Риману монотонной функции.

Теорема 1:

Если функция монотонна на отрезке , то она интегрируема на этом отрезке.

Доказательство:

Возьмем произвольное разбиение

Рассмотрим разность между верхней и нижней суммой Дарбу, пусть для определенности f не убывает на , тогда мы получим, что

Получим, что разность между верхней и нижней суммой Дарбу

Теорема доказана.

Билет 33

Свойства определенного интеграла.

Билет 34

Интеграл с переменным верхним пределом, его непрерывность.

Рассмотрим функцию , интегрируемую на отрезке. По аддитивному свойству интеграла:

, можно найти отрезок на котором представляется возможным рассмотреть функцию.

Теорема:

Если функция интегрируема на отрезке, тонепрерывна на отрезке.

Доказательство:

Рассмотрим функцию ,

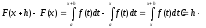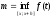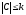, где ,,, где

Теорема доказана.

Билет 35

Дифференцируемость интеграла с переменным верхним пределом.

Теорема:

Пусть функция интегрируема на отрезке, непрерывна в точке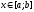, тогда функциядифференцируема в точкеи.

Доказательство:

,

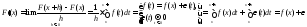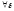
, , т.е.

.

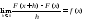Теорема доказана.

Следствие:

Если функция 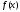непрерывна на отрезке, то, т.е.- первообразная.

,

Функция непрерывна в точк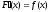е,;, гденепрерывна на отрезке. Заключаем, что.

Т.е. любая непрерывная функция имеет первообразную.

Теорема доказана.

Билет 36

Формула Ньютона-Лейбница

Билет 37

Замена переменной в определенном интеграле.

Билет 38

Интегрирование по частям определенного интеграла.

Билет 39

Теорема о среднем для определенного интеграла.