
Лекции - Ржавинская / rzhavinskaya_lektsii / Лекция_9
.docЛекция 9
Исследование и решение произвольной системы линейных уравнений
|
Правило Крамера. Исследование произвольной системы линейных алгебраических уравнений. Системы линейных однородных уравнений. Фундаментальная система решений |
9.1. Правило Крамера
Пусть дана система
![]() линейных алгебраических уравнений с
линейных алгебраических уравнений с
![]() неизвестными:
неизвестными:
 (9.1)
(9.1)
Обозначим
![]() ,
,
![]() .
.
![]() будем называть определителем системы
(9.1).
будем называть определителем системы
(9.1).
Обозначим
 ,
,
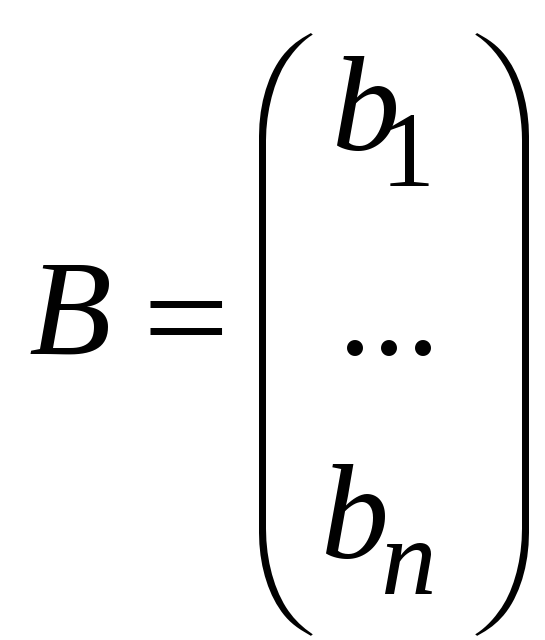 .
Система (9.1) равносильна матричному
уравнению
.
Система (9.1) равносильна матричному
уравнению
![]() .
(9.2)
.
(9.2)
Теорема 1. Если
![]() ,
то система (9.1) имеет, притом
единственное, решение.
,
то система (9.1) имеет, притом
единственное, решение.
Доказательство. Так как
![]() ,
то
,
то
![]() .
Умножим обе части (9.2) на
.
Умножим обе части (9.2) на
![]() слева:
слева:
![]() .
.
Итак, решением матричного уравнения
(9.2) является матрица
![]() - матричное уравнение (9.2) имеет решение,
следовательно, система (9.1) совместна.
- матричное уравнение (9.2) имеет решение,
следовательно, система (9.1) совместна.
![]()
 (9.3)
(9.3)
Решение системы (9.1) дается формулами
(9.3), и так как
![]() ,
,
![]() ,
вполне определенные числа, единственно.
,
вполне определенные числа, единственно.
Теорема доказана.
Правило Крамера: если
![]() ,
то решение системы (9.1) может быть
найдено по формулам
,
то решение системы (9.1) может быть
найдено по формулам
![]() ,
,
![]() ,
где
,
где
![]() - определитель, который получится из
- определитель, который получится из
![]() ,
если столбец коэффициентов при
,
если столбец коэффициентов при
![]() заменить столбцом свободных членов.
заменить столбцом свободных членов.
Пример 1. По правилу Крамера, если оно применимо, решить систему
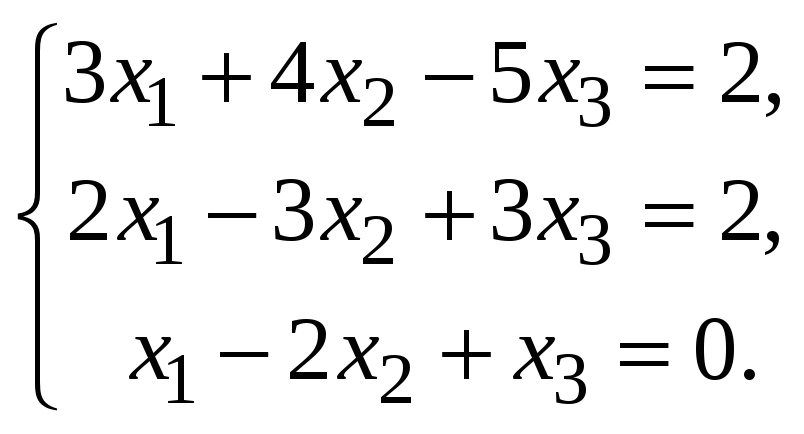
Решение. Имеем
 ,
,
следовательно, правило Крамера применимо.
 ,
,
 ,
,
 .
.
По формулам (9.3) находим
![]() ,
,
![]() ,
,
![]() .
.
9.2. Исследование произвольной системы
линейных уравнений
Пусть дана система
![]() уравнений с
уравнений с
![]() неизвестными:
неизвестными:
 (9.4)
(9.4)
Обозначим матрицу из коэффициентов
![]()
 .
.
Матрица
![]() содержит матрицу
содержит матрицу
![]() и еще столбец свободных членов, она
называется расширенной матрицей
по отношению к
и еще столбец свободных членов, она
называется расширенной матрицей
по отношению к
![]() :
:
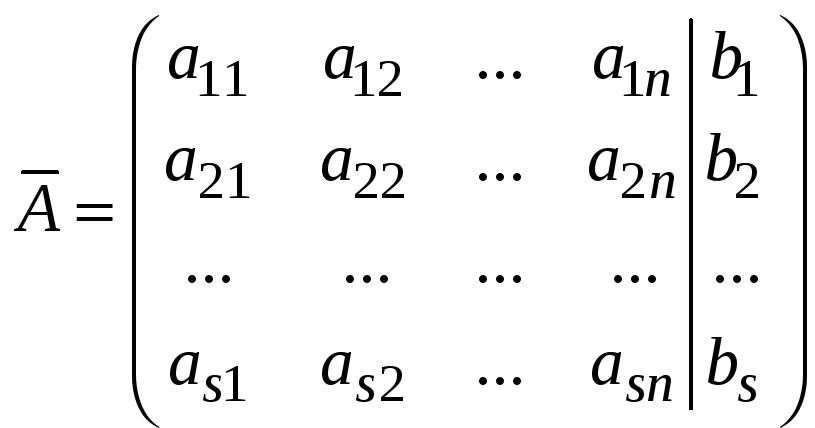 .
.
Теорема 2 (Кронекера - Капелли).
Система совместна тогда и только
тогда, когда
![]() .
.
Доказательство.
Необходимость. Пусть система (9.4)
совместна и
![]() - решение (9.4), следовательно,
справедливы тождества
- решение (9.4), следовательно,
справедливы тождества
 (9.5)
(9.5)
В матрице
![]() к последнему столбцу прибавим первый,
умноженный на
к последнему столбцу прибавим первый,
умноженный на
![]() ,
второй, умноженный на
,
второй, умноженный на
![]() ,…,
,…,
![]() -й,
умноженный на
-й,
умноженный на
![]() Получим, учитывая (9.5),
Получим, учитывая (9.5),
![]() ~
~ .
.
Поскольку выполнялись элементарные
преобразования, то
![]() ,
но
,
но
![]() (добавление столбца из нулей не может
изменить ранга), отсюда
(добавление столбца из нулей не может
изменить ранга), отсюда
![]() .
.
Достаточность.
Пусть
![]() .
Это означает, что существует минор
.
Это означает, что существует минор
![]() порядка
порядка
![]() ,
а все миноры порядка
,
а все миноры порядка
![]() ,
окаймляющие
,
окаймляющие
![]() ,
равны нулю.
,
равны нулю.
Пусть
![]() расположен в левом верхнем углу матрицы
расположен в левом верхнем углу матрицы
![]() (это предположение не ограничивает
общности рассуждений, так как можно
переставить уравнения и перенумеровать
неизвестные и тем самым добиться того,
что
(это предположение не ограничивает
общности рассуждений, так как можно
переставить уравнения и перенумеровать
неизвестные и тем самым добиться того,
что
![]() будет расположен в первых
будет расположен в первых
![]() строках и первых
строках и первых
![]() столбцах матрицы
столбцах матрицы
![]() ):
):
 .
.
Тогда первые
![]() строк матрицы линейно независимы, а
остальные
строк матрицы линейно независимы, а
остальные
![]() строк являются их линейной комбинацией
(теорема о базисном миноре), следовательно,
через первые
строк являются их линейной комбинацией
(теорема о базисном миноре), следовательно,
через первые
![]() уравнений линейно выражаются остальные
уравнений линейно выражаются остальные
![]() уравнений. Таким образом, вся система
(9.4) эквивалентна первым
уравнений. Таким образом, вся система
(9.4) эквивалентна первым
![]() уравнениям:
уравнениям:
 (9.6)
(9.6)
Случай 1:
![]() .
Система (9.6) имеет единственное решение
(определитель системы (9.6)
.
Система (9.6) имеет единственное решение
(определитель системы (9.6)
![]() ,
- применяем теорему 1). Его можно найти,
например, по правилу Крамера.
,
- применяем теорему 1). Его можно найти,
например, по правилу Крамера.
Случай 2:
![]() .
Перепишем (9.6) в виде
.
Перепишем (9.6) в виде
 (9.7)
(9.7)
Неизвестные
![]() назовем главными,
назовем главными,
![]() - свободными.
- свободными.
Присвоим свободным неизвестным
произвольные числовые значения, положим
![]() .
Тогда согласно теореме 1 из системы
(9.7) определится единственный набор
.
Тогда согласно теореме 1 из системы
(9.7) определится единственный набор
![]() главных неизвестных. Таким образом,
набор
главных неизвестных. Таким образом,
набор
![]() чисел
чисел
![]() ,
,
![]() является решением системы (9.4).
является решением системы (9.4).
Значения свободных неизвестных можно выбрать бесчисленным множеством способов, поэтому система (9.4) имеет бесчисленное множество решений.
И в случае 1, и в случае 2 система оказалась совместной. Достаточность доказана.
Определение 1. Формула, выражающая
решение системы (9.4) в виде вектор-функции
![]() свободных неизвестных, называется
общим решением системы (9.4):
свободных неизвестных, называется
общим решением системы (9.4):
 .
.
Пример 2. Исследовать совместность системы и, если система совместна, найти общее решение и одно частное:
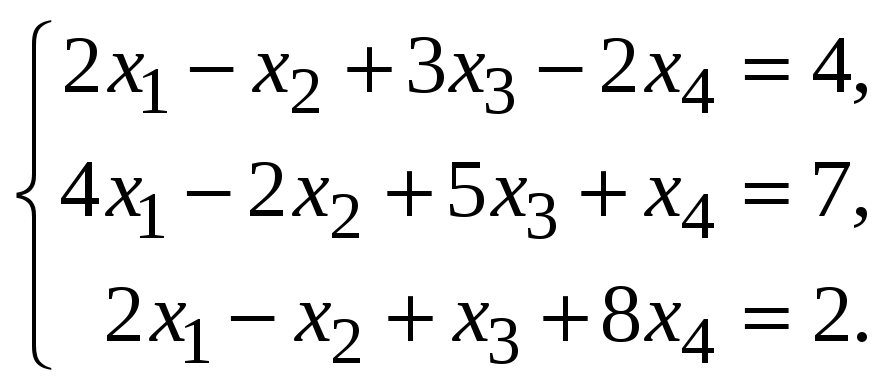
Решение. Найдем ранг матриц
![]() и
и
![]() :
:
 ~
~ ~
~
~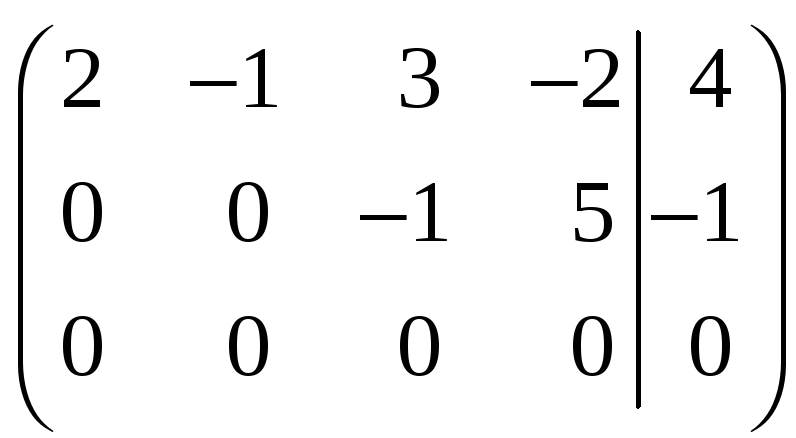 .
.
Итак,
![]() (минор второго порядка
(минор второго порядка
![]() ,
все миноры, его окаймляющие, равны нулю
и в
,
все миноры, его окаймляющие, равны нулю
и в
![]() ,
и в
,
и в
![]() ).
Следовательно, согласно теореме 2 система
совместна.
).
Следовательно, согласно теореме 2 система
совместна.
Так как
![]() ,
система имеет бесчисленное множество
решений.
,
система имеет бесчисленное множество
решений.
Вся система эквивалентна системе первых двух уравнений:
![]()
В качестве главных неизвестных возьмем
![]() и
и
![]() (
(![]() ),
свободных -
),
свободных -
![]() и
и
![]() и перепишем систему в виде
и перепишем систему в виде
![]() -
-
"укороченная" система.
Отсюда
![]() и
и
![]() .
.
Общее решение
 .
.
Частное решение получим, присвоив
конкретные числовые значения свободным
неизвестным, например,
![]() ,
тогда
,
тогда
 .
.
9.3. Системы линейных однородных
алгебраических уравнений
Пусть дана система линейных однородных уравнений
 (9.8)
(9.8)
Система (9.8) всегда совместна (решение
![]() всегда присутствует среди решений).
всегда присутствует среди решений).
Если
![]() ,
то это решение - единственное, если
,
то это решение - единственное, если
![]() ,
система (9.8) имеет бесчисленное множество
решений (и, следовательно, есть решения,
отличные от
,
система (9.8) имеет бесчисленное множество
решений (и, следовательно, есть решения,
отличные от
![]() ).
).
Теорема 3. Любая линейная комбинация решений системы однородных линейных уравнений (9.8) является решением системы (9.8).
Доказательство. Пусть
 и
и
 - произвольные решения системы (9.8).
- произвольные решения системы (9.8).
Пусть
![]() - некоторое число,
- некоторое число,
![]() .
Подставим
.
Подставим

в
![]() -е
уравнение системы (9.8):
-е
уравнение системы (9.8):
![]()
![]()
![]() удовлетворяет
удовлетворяет
![]() -му
уравнению системы (9.8) при произвольном
-му
уравнению системы (9.8) при произвольном
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() является решением (9.8).
является решением (9.8).
Пусть
![]() - произвольное вещественное число,
- произвольное вещественное число,
 .
.
Подставим
![]() в
в
![]() -е
уравнение системы (9.8),
-е
уравнение системы (9.8),
![]() :
:
![]()
![]() - решение (9.8).
- решение (9.8).
Итак, сумма любых двух решений системы (9.8) и произведение любого решения на число являются решениями системы (9.8), следовательно, любая линейная комбинация решений системы (9.8) является решением.
Определение 2. Пусть дана система
линейных однородных уравнений с n
неизвестными
![]() и матрицей
и матрицей
![]() ,
,
![]() .
Пусть неизвестные
.
Пусть неизвестные
![]() являются свободными.
являются свободными.
Обозначим через
![]() ,
,
![]() ,
то единственное решение системы, которое
получится, если неизвестному
,
то единственное решение системы, которое
получится, если неизвестному
![]() присвоить значение
присвоить значение
![]() ,
а остальным свободным неизвестным -
значение
,
а остальным свободным неизвестным -
значение
![]() .
.
Система решений
![]() называется фундаментальной системой
решений данной системы линейных
однородных уравнений.
называется фундаментальной системой
решений данной системы линейных
однородных уравнений.
Справедливо следующее утверждение, которое приведем без доказательства.
Теорема 4. Пусть дана система
линейных однородных уравнений с матрицей
![]() ,
,
![]() ,
и
,
и
![]() - фундаментальная система решений. Тогда
всякое решение системы является линейной
комбинацией решений
- фундаментальная система решений. Тогда
всякое решение системы является линейной
комбинацией решений
![]() .
.
Пример 3. Найти общее решение и фундаментальную систему решений системы
![]() (9.9)
(9.9)
Решение. Первое уравнение,
умноженное на
![]() ,
прибавим ко второму:
,
прибавим ко второму:
![]()
Отсюда
![]() .
.
Общее решение
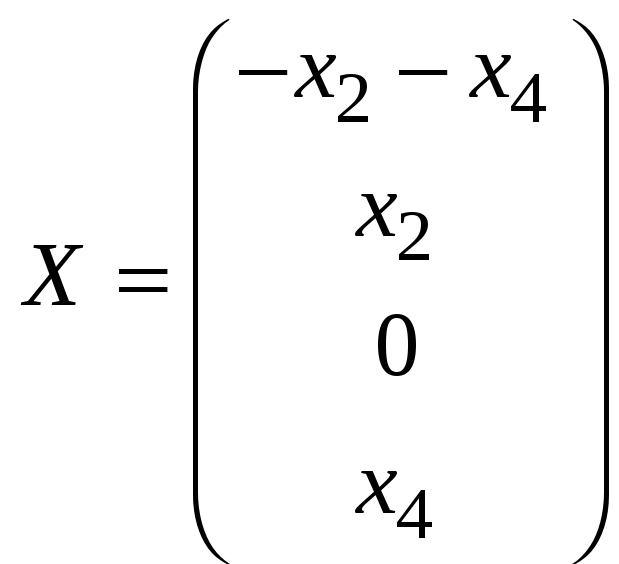 ,
,
свободными являются неизвестные
![]() и
и
![]() ,
главными -
,
главными -
![]() и
и
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы
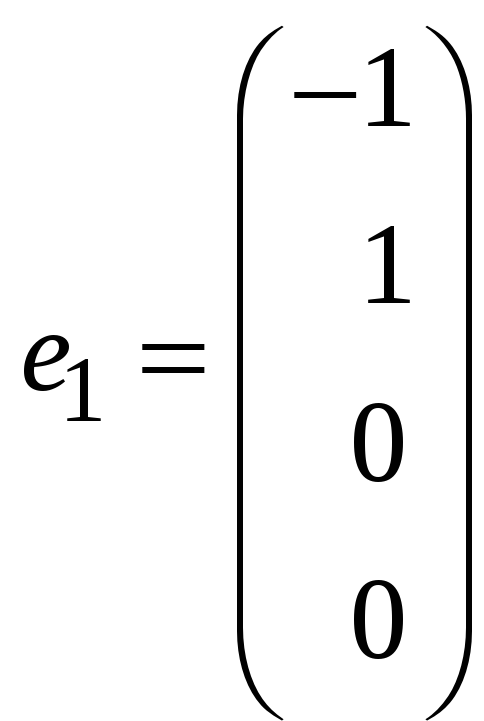 и
и
 составляют фундаментальную систему
решений системы (9.9)
составляют фундаментальную систему
решений системы (9.9)
![]() .
.
Последнее равенство можно проверить непосредственно.
