
Лекции - Ржавинская / rzhavinskaya_lektsii / Лекция_11
.docЛекция 11
Связь между базисами линейного пространства.
Линейные подпространства
|
Матрица перехода от базиса к базису. Связь координат одного и того же вектора в двух базисах. Линейные подпространства. Примеры |
11.1. Связь между базисами линейного пространства
Пусть
![]() -
линейное пространство,
-
линейное пространство,
![]() (I)
и
(I)
и
![]() (II)
- два базиса в
(II)
- два базиса в
![]() .
.
Так как (I)
- базис, любой вектор из
![]() ,
в частности любой вектор системы (II),
можно представить в виде линейной
комбинации векторов системы (I),
т.е. найдутся такие числа
,
в частности любой вектор системы (II),
можно представить в виде линейной
комбинации векторов системы (I),
т.е. найдутся такие числа
![]() ,
что
,
что
![]()
![]()
………………………………. (11.1)
![]()
Определение 1.
Матрица
![]() называется матрицей перехода от базиса
(I) к базису (II).
называется матрицей перехода от базиса
(I) к базису (II).
Замечание
1. Столбцы матрицы перехода
![]() ,
являются координатами в разложении
векторов
,
являются координатами в разложении
векторов
![]() по базису (I).
по базису (I).
Справедливость этого замечания непосредственно следует из равенств (11.1).
Замечание 2. Матрица перехода от базиса к базису является невырожденной матрицей.
Доказательство этого факта опустим.
Справедливо следующее утверждение.
Теорема 1. Пусть
![]() - линейное пространство,
- линейное пространство,
![]() (I) и
(I) и
![]() (II) - два базиса в
(II) - два базиса в
![]() ,
,
![]() - матрица перехода от (I)
к (II),
- матрица перехода от (I)
к (II),
![]() ,
,
![]() и
и
![]() ,
тогда
,
тогда
 .
(11.2)
.
(11.2)
Доказательство.
Подставим в разложение
![]() по базису (II) выражения
по базису (II) выражения
![]() из (11.1), получим
из (11.1), получим


![]() .
.
Последнюю сумму запишем развернуто:
![]()
![]()
![]() .
.
По условию
![]() ,
используя теорему о единственности
разложения вектора по базису (теорема
3 в лекции 10), получим
,
используя теорему о единственности
разложения вектора по базису (теорема
3 в лекции 10), получим
![]() ,
,
![]() ,
,
……………………………………
![]() ,
,
что в матричном виде выглядит как равенство
 .
.
Отсюда следует
 .
.
Теорема доказана.
Пример
1.
![]() - линейное пространство всех геометрических
векторов плоскости,
- линейное пространство всех геометрических
векторов плоскости,
![]() (I)
- произвольный декартов базис,
(I)
- произвольный декартов базис,
![]() (II)
- декартов базис, полученный поворотом
векторов
(II)
- декартов базис, полученный поворотом
векторов
![]() и
и
![]() на угол
на угол
![]() против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).
против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).
Имеем
![]() ,
,
![]() (рис. 11.1). Тогда
(рис. 11.1). Тогда
![]()
 .
.
![]() - матрица перехода
от (I) к (II).
- матрица перехода
от (I) к (II).
Найдем
![]() .
.
![]() и
и
![]() .
.
Формула (11.2) в этом случае имеет вид
![]() ,
,
где
![]() - координаты произвольного вектора
- координаты произвольного вектора
![]() в базисе (I), а
в базисе (I), а
![]() – координаты этого же вектора в базисе
(II).
– координаты этого же вектора в базисе
(II).
(Сравните с формулами (5.24) в Лекции 5).
Пример
2.
![]() - произвольное линейное пространство,
- произвольное линейное пространство,
![]() .
Векторы
.
Векторы
![]() ,
,![]() и
и
![]() заданы своими координатами в некотором
базисе
заданы своими координатами в некотором
базисе
![]() .
Доказать, что система
.
Доказать, что система
![]() - базис в
- базис в
![]() ,
и найти координаты вектора
,
и найти координаты вектора
![]() в базисе
в базисе
![]() .
.
Сначала докажем,
что система
![]() - базис. Рассмотрим линейную комбинацию
векторов
- базис. Рассмотрим линейную комбинацию
векторов
![]() и
и
![]() ,
равную нулевому вектору
,
равную нулевому вектору
![]() :
:
![]() .
.
Покоординатно последнее равенство запишется в виде системы двух уравнений:
![]() (11.3)
(11.3)
Определитель
системы (11.3)
![]() ,
следовательно, система (11.3) имеет
единственное решение
,
следовательно, система (11.3) имеет
единственное решение
![]() .
.
Итак, допустив,
что линейная комбинация векторов
![]() и
и
![]() равна
равна
![]() ,
мы с необходимостью получили, что
коэффициенты этой линейной комбинации
равны нулю. Это означает, что система
векторов
,
мы с необходимостью получили, что
коэффициенты этой линейной комбинации
равны нулю. Это означает, что система
векторов
![]() линейно независима, а так как
линейно независима, а так как
![]() ,
векторы
,
векторы
![]() являются базисом в
являются базисом в
![]() .
Обозначим этот базис (II).
.
Обозначим этот базис (II).
Найдем матрицу перехода от (I) к (II).
В силу определения
1
![]() (координаты векторов
(координаты векторов
![]() и
и
![]() в (I) располагаем по
столбцам).
в (I) располагаем по
столбцам).
Обозначим через
![]() координаты
вектора
координаты
вектора
![]() в (II).
в (II).
Воспользуемся
теоремой 1. Найдем
![]() .
Имеем
.
Имеем
![]() ,
,
![]()
и по формуле (11.2) получим
![]() .
.
Итак,
![]() .
.
Упражнения.
1.
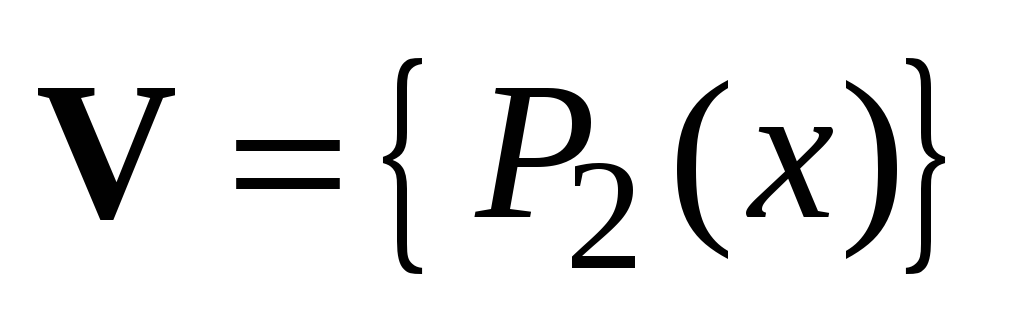 - линейное пространство многочленов
степени
- линейное пространство многочленов
степени
 .
Доказать, что система многочленов
.
Доказать, что система многочленов
 образует базис в
образует базис в
 .
Найти матрицу перехода от базиса
.
Найти матрицу перехода от базиса
 к этому базису и координаты многочлена
к этому базису и координаты многочлена
 в нем.
в нем.
2. В произвольном
линейном пространстве векторы
![]() и
и
![]() заданы своими координатами в некотором
базисе
заданы своими координатами в некотором
базисе
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Доказать, что система векторов
.
Доказать, что система векторов
![]() - базис в
- базис в
![]() ,
и найти координаты
,
и найти координаты
![]() в этом базисе.
в этом базисе.
3. В произвольном
линейном пространстве
![]() векторы
векторы
![]() (I)
и
(I)
и
![]() (II)
заданы своими координатами в некотором
базисе
(II)
заданы своими координатами в некотором
базисе
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Доказать, что системы (I)
и (II) являются базисами в
.
Доказать, что системы (I)
и (II) являются базисами в
![]() ,
и найти матрицу перехода от (I)
к (II).
,
и найти матрицу перехода от (I)
к (II).
11.2. Линейные подпространства
Определение 2.
Пусть
![]() - линейное пространство. Непустое
подмножество
- линейное пространство. Непустое
подмножество
![]() линейного пространства
линейного пространства
![]() (
(![]() )
называется линейным подпространством
в
)
называется линейным подпространством
в
![]() ,
если выполняются два условия:
,
если выполняются два условия:
1)
![]() ;
;
2)
![]() при любом вещественном числе
при любом вещественном числе
![]() .
.
Пример
3. Пусть
![]() - линейное пространство всех
арифметических
- линейное пространство всех
арифметических
![]() -мерных
векторов
-мерных
векторов
![]() ;
;
![]() - совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
- совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
![]() .
.
![]() - подпространство в
- подпространство в
![]() .
.
Действительно,
пусть
![]() и
и
![]() ,
следовательно, по определению
,
следовательно, по определению
![]()
![]() и
и
![]() .
По правилу сложения векторов в
.
По правилу сложения векторов в
![]()
![]() и, таким образом, сумма любых двух
векторов из
и, таким образом, сумма любых двух
векторов из
![]() принадлежит
принадлежит
![]() .
.
Пусть
![]() и
и
![]() - произвольное вещественное число.
Но
- произвольное вещественное число.
Но
![]() (так как
(так как
![]() ),
следовательно, по правилу умножения
вектора на число в
),
следовательно, по правилу умножения
вектора на число в
![]()
![]() и вместе с любым вектором произведение
его на
и вместе с любым вектором произведение
его на
![]() тоже принадлежит
тоже принадлежит
![]() .
В соответствии с определением 2 это
означает, что
.
В соответствии с определением 2 это
означает, что
![]() - линейное подпространство в
- линейное подпространство в
![]() .
.
Замечание.
Если
![]() - линейное
подпространство в
- линейное
подпространство в
![]() ,
то
,
то
![]() само является
линейным пространством относительно
введенных в
само является
линейным пространством относительно
введенных в
![]() операций
сложения и умножения на число.
операций
сложения и умножения на число.
Действительно,
требования 1) и 2) в определении 2 означают,
что в
![]() определены операции сложения векторов
и умножения вектора на число.
определены операции сложения векторов
и умножения вектора на число.
Аксиомы 1 и 2
выполняются в
![]() ,
так как они имеют место в
,
так как они имеют место в
![]() .
Убедимся в справедливости аксиомы 3.
.
Убедимся в справедливости аксиомы 3.
Пусть
![]() ,
,
![]() ,
следовательно, согласно условию 2)
,
следовательно, согласно условию 2)
![]() ,
но по следствию 5 из аксиом в
,
но по следствию 5 из аксиом в
![]()
![]() ,
таким образом,
,
таким образом,
![]() и в
и в
![]() справедлива аксиома 3.
справедлива аксиома 3.
Пусть
![]() ,
,
![]() .
Следовательно, согласно условию 2)
.
Следовательно, согласно условию 2)
![]() ,
но по следствию 8 из аксиом в
,
но по следствию 8 из аксиом в
![]()
![]() ,
таким образом,
,
таким образом,
![]() и в
и в
![]() справедлива аксиома 4.
справедлива аксиома 4.
Аналогично
проверяется справедливость аксиом 5 -
8, следовательно,
![]() - линейное пространство.
- линейное пространство.
Пусть
![]() - произвольное линейное пространство,
- произвольное линейное пространство,
![]() - некоторая система векторов в
- некоторая система векторов в
![]() .
Рассмотрим совокупность всех векторов
вида
.
Рассмотрим совокупность всех векторов
вида
![]() ,
где
,
где
![]() принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
![]() .
.
![]() называется линейной оболочкой
векторов
называется линейной оболочкой
векторов
![]() .
.
![]() является подпространством в
является подпространством в
![]() .
.
Действительно,
![]() (так как, например, сами векторы
(так как, например, сами векторы
![]() ,
,
![]() ,
принадлежат
,
принадлежат
![]() ).
).
Пусть
![]() ,
,
![]() ,
следовательно, по определению
,
следовательно, по определению
![]()
![]() такие, что
такие, что
![]() ,
,
![]() .
.
Имеем
![]() и
и
![]() .
.
Пусть
![]() ,
,
![]() - произвольное вещественное число.
- произвольное вещественное число.
Имеем
![]() и
и
![]() .
.
Таким образом,
выполняются условия 1) и 2) определения
2 и
![]() является линейным подпространством
в
является линейным подпространством
в
![]() .
.
Говорят, что
![]() порождено системой векторов
порождено системой векторов
![]() или
или
![]() "натянуто" на систему
"натянуто" на систему
![]() .
.
Заметим, что само
линейное пространство
![]() может рассматриваться как линейная
оболочка любого своего базиса.
может рассматриваться как линейная
оболочка любого своего базиса.
Пример
4.
![]() Найти
размерность и базис линейной оболочки
векторов
Найти
размерность и базис линейной оболочки
векторов
![]() ,
,
![]() ,
,
![]() .
.
Найдем ранг матрицы,
строками которой являются данные векторы
![]() ,
,
![]() ,
,
![]() :
:
 ~
~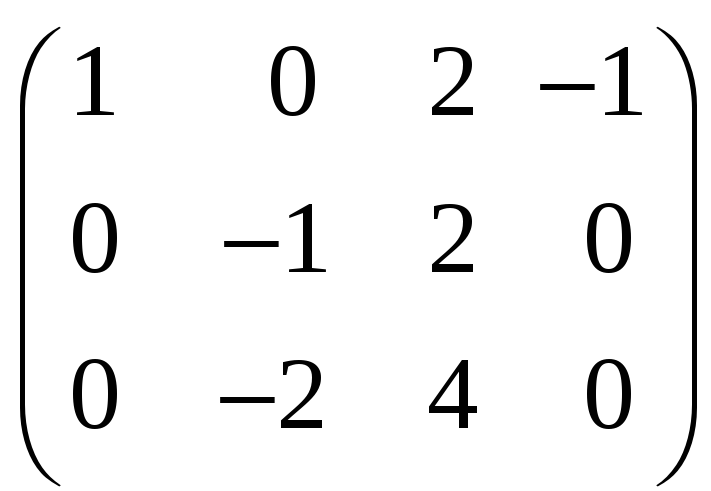 ~
~ .
.
Минор второго
порядка
![]() ,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы
,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы
![]() и
и
![]() составляют линейно независимую систему
векторов в
составляют линейно независимую систему
векторов в
![]() ,
а следовательно, и в линейной оболочке
,
а следовательно, и в линейной оболочке
![]() ,
и вектор
,
и вектор
![]() через них линейно выражается. Тогда
любой вектор
через них линейно выражается. Тогда
любой вектор
![]() тоже линейно выражается через
тоже линейно выражается через
![]() и
и
![]() .
Векторы
.
Векторы
![]() и
и
![]() являются базисом в
являются базисом в
![]() ,
,
![]() .
.
Упражнение.
![]() -
линейное пространство арифметических
векторов
-
линейное пространство арифметических
векторов
![]() .
Найти размерность и все
базисы линейной оболочки векторов
.
Найти размерность и все
базисы линейной оболочки векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
