
Лекция 12 Линейные операторы
|
Линейный оператор - определение и примеры. Матрица линейного оператора. Собственные числа и собственные векторы. Линейные операторы с простым спектром |
12.1. Понятие линейного оператора
Определение
1. Пусть
![]() - линейное пространство и каждому вектору
- линейное пространство и каждому вектору![]() ,
принадлежащему
,
принадлежащему![]() ,
поставлен в соответствие вектор
,
поставлен в соответствие вектор
![]() ,
,
![]() .
Соответствие
.
Соответствие![]() называется оператором,
определенным в линейном пространстве
называется оператором,
определенным в линейном пространстве
![]() .
.
Принята
также запись:
![]() .
Вектор
.
Вектор![]() называетсяпрообразом,
а
называетсяпрообразом,
а
![]() -образом
при отображении оператором
-образом
при отображении оператором
![]() .
.
Определение
2.
Оператор
![]() ,
определенный в линейном пространстве
,
определенный в линейном пространстве
![]() ,
называется линейным,
если:
,
называется линейным,
если:
1)
![]() ;
;
2)
![]()
![]() - вещественного числа
- вещественного числа![]() .
.
П ример
1.
ример
1.
![]() -
линейное пространство всех геометрических
векторов плоскости,
-
линейное пространство всех геометрических
векторов плоскости,
![]() - зеркальное отражение относительно
оси
- зеркальное отражение относительно
оси![]() (рис. 12.1).
(рис. 12.1).![]() - линейный оператор.
- линейный оператор.
Убедимся, что выполняется требование 2) в определении 2.
Пусть
![]() - произвольное вещественное число, по
определению умножения на
- произвольное вещественное число, по
определению умножения на![]() для геометрического вектора
для геометрического вектора![]() вектор
вектор![]() имеет то же направление, что и
имеет то же направление, что и![]() ,
если
,
если![]() ,
и противоположное, если
,
и противоположное, если![]() ,
и
,
и![]() .
.
Рис.
12.2 соответствует случаю
![]() ,
,![]() (
(![]() рассматривается аналогично).
рассматривается аналогично).
П усть
усть![]() ,
,![]() ,
,![]() - зеркальное отражение вектора
- зеркальное отражение вектора![]() относительно оси
относительно оси![]() ,
,![]() - зеркальное отражение вектора
- зеркальное отражение вектора![]() .
Тогда
.
Тогда![]() ~
~![]() и, значит,
и, значит,![]() .
Но
.
Но![]() ,
поэтому
,
поэтому![]() .
Кроме того, направление вектора
.
Кроме того, направление вектора![]() совпадает с направлением вектора
совпадает с направлением вектора![]() ,
следовательно,
,
следовательно,![]() .
Таким образом, имеем
.
Таким образом, имеем
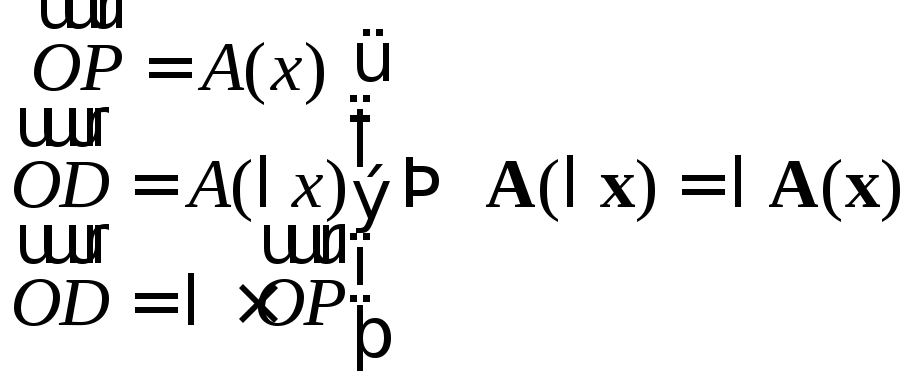 .
.
Так
же, исходя из геометрических соображений,
можно доказать, что
![]() ,
следовательно, оператор
,
следовательно, оператор![]() зеркального отражения относительно
оси
зеркального отражения относительно
оси![]() является линейным оператором.
является линейным оператором.
Упражнения.
1.
![]() -
линейное пространство всех многочленов
степени
-
линейное пространство всех многочленов
степени![]() ,
,![]() - оператор дифференцирования,
- оператор дифференцирования,![]() .
Доказать, что
.
Доказать, что![]() - линейный оператор.
- линейный оператор.
2.
![]() -
линейное пространство всех непрерывных
на отрезке
-
линейное пространство всех непрерывных
на отрезке![]() функций. Для любой
функций. Для любой![]() оператор
оператор![]() определен следующим равенством:
определен следующим равенством:
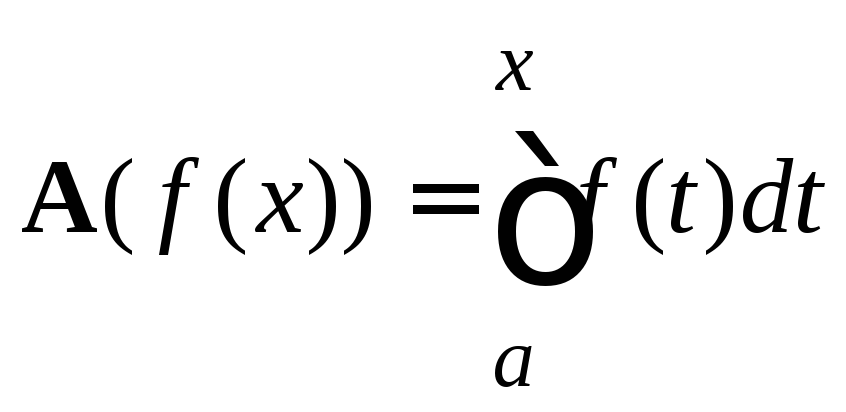 ,
,
![]() .
.
Доказать,
что
![]() - линейный оператор.
- линейный оператор.
Определение
3.
Пусть
![]() -
линейное пространство,
-
линейное пространство,
![]() -
базис в
-
базис в![]() ,
,
![]() -
линейный оператор в
-
линейный оператор в![]() .
Матрицей линейного оператора
.
Матрицей линейного оператора![]() в базисе
в базисе![]() называется матрица
называется матрица![]() ,
,
![]() ,такая,
что
,такая,
что
![]() ,
,
![]() ,
,
…………………………………….. (12.1)
![]() .
.
Замечание
1.
Столбцы матрицы
![]() являются координатами в разложении
векторов
являются координатами в разложении
векторов![]() по базису
по базису![]() .
.
П ример
2.
Найти
матрицу линейного оператора зеркального
отражения относительно оси
ример
2.
Найти
матрицу линейного оператора зеркального
отражения относительно оси
![]() в базисе
в базисе![]() .
.
По
определению оператора
![]()
![]() (рис. 12.3).
(рис. 12.3).
Используя
разложение векторов
![]() и
и![]() по базису
по базису![]() ,
находим:
,
находим:![]() ,
,![]() .
Полученные строки координат располагаем
по столбцам:
.
Полученные строки координат располагаем
по столбцам:
![]() .
.
Упражнение.
![]() -
линейное пространство всех геометрических
векторов,
-
линейное пространство всех геометрических
векторов,
![]() - декартов базис,
- декартов базис,![]() - декартова система координат,
- декартова система координат,![]() - оператор проектирования на ось
- оператор проектирования на ось![]() .
Доказать, что
.
Доказать, что![]() -
линейный оператор, и найти его матрицу
в базисе
-
линейный оператор, и найти его матрицу
в базисе![]() .
.
Замечание
2.
Пусть
![]() -
линейное пространство,
-
линейное пространство,![]() -
линейный оператор в
-
линейный оператор в![]() ,
,![]() (I)
- базис в
(I)
- базис в
![]() .
Матрица оператора в базисе (I)
определена однозначно.
.
Матрица оператора в базисе (I)
определена однозначно.
Для
того, чтобы в этом убедиться, разложим
векторы
![]() по базису (I).
Столбцы матрицы
по базису (I).
Столбцы матрицы
![]() представляют собой координаты этих
векторов, которые согласно теореме 3
лекции 10 определяются единственным
образом, следовательно, матрица
представляют собой координаты этих
векторов, которые согласно теореме 3
лекции 10 определяются единственным
образом, следовательно, матрица![]() оператора
оператора![]() в (I)
определена однозначно.
в (I)
определена однозначно.
Теорема
1.
Пусть
![]() -
линейное пространство,
-
линейное пространство,
![]() (I)
- базис в
(I)
- базис в
![]() ,
,
![]() -
линейный оператор в
-
линейный оператор в![]() ,
,
![]() - матрица линейного оператора
- матрица линейного оператора![]() в базисе(I),
в базисе(I),
![]() ,
,
![]() ,
,
![]() ,
,![]() .
Тогда
.
Тогда
 .
.
Доказательство. Имеем
![]()
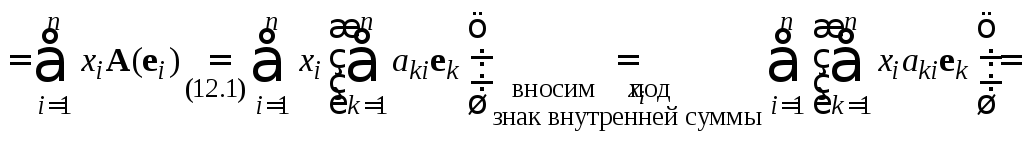
 .
.
По
условию
![]() .
.
Используя теорему о единственности разложения вектора по базису (теорема 3 из лекции 10), получим
![]() .
(12.2)
.
(12.2)
Заметим,
что в последнем равенстве числа
![]() - элементыk-й
строки матрицы
- элементыk-й
строки матрицы
![]() .
.
Привлекая правило умножения матриц, равенство (12.2) запишем в виде
 .
.
Теорема доказана.
Пример
3.
Для линейного оператора зеркального
отражения относительно оси
![]() найти, как преобразуются координаты
произвольного вектора.
найти, как преобразуются координаты
произвольного вектора.
Решение. Матрица оператора была найдена в примере 2:
![]()
 .
.
В
силу теоремы 1, если
![]() - прообраз, а
- прообраз, а![]() - образ,
- образ,![]() ,
то
,
то![]() ,
т.е. первая координата образа остается
без изменения, а вторая меняет лишь знак
(рис. 12.4).
,
т.е. первая координата образа остается
без изменения, а вторая меняет лишь знак
(рис. 12.4).
Пример
4.
![]() -
линейное пространство всех многочленов
степени
-
линейное пространство всех многочленов
степени![]() ,
,![]() -
линейный оператор дифференцирования.
Найти его матрицу в базисе
-
линейный оператор дифференцирования.
Найти его матрицу в базисе![]() и, используя теорему 1, продифференцировать
многочлен
и, используя теорему 1, продифференцировать
многочлен![]() .
.
Решение.
Находим
образы векторов базиса
![]() и разлагаем полученные векторы по базису
и разлагаем полученные векторы по базису![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Матрица
оператора
![]() в базисе
в базисе![]() имеет вид
имеет вид
 ,
,
а
вектор
 .
Обозначим
.
Обозначим .
По теореме 1 имеем
.
По теореме 1 имеем
 ,
,
или
в виде разложения по базису
![]() :
:![]() .
.
Упражнение.
![]() -
линейное пространство всех геометрических
векторов плоскости,
-
линейное пространство всех геометрических
векторов плоскости,![]() -
декартов базис,
-
декартов базис,![]() -
декартова система координат,
-
декартова система координат,![]() -
оператор поворота плоскости вокруг
начала координат на угол
-
оператор поворота плоскости вокруг
начала координат на угол![]() против часовой стрелки. Доказать, что
против часовой стрелки. Доказать, что![]() - линейный оператор, найти матрицу
- линейный оператор, найти матрицу![]() оператора
оператора![]() в базисе
в базисе![]() и координаты образа вектора
и координаты образа вектора![]() .
.
