3.6. Нормированное уравнение прямой. Расстояние от точки до прямой

Пусть задана декартова система координат,- произвольная прямая (рис. 3.14). Проведем черезпрямую,, точку пересечениясобозначим.

Рассмотрим вектор :приложен к точке,, направлениесовпадает с направлением вектора(если, направлениевыберем произвольно). Обозначим черезугол наклонак оси. Тогда. Длинуобозначим через:. Имеем

; (3.19)

; (3.20)

. (3.21)

Из (3.19), (3.20) и (3.21) получим: или

. (3.22)

Уравнение (3.22) называется нормированным уравнением прямой (- угол наклона вектора,) к оси,- расстояние от начала координатдо).

Приведем без доказательства следующее утверждение.

Теорема 3. Расстояние от точки до прямойравно абсолютной величине результата подстановки координат этой точк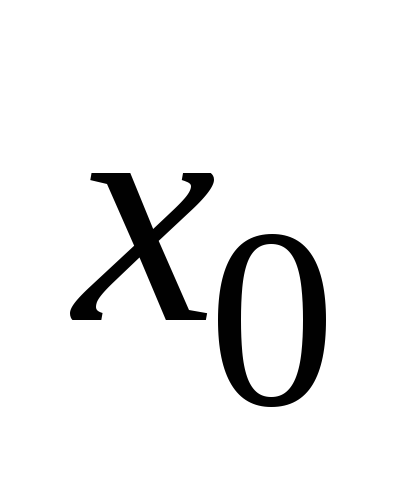иив левую часть нормированного уравнения прямой:

.

Замечание. Если прямая задана общим уравнением

, (3.23)

то для перехода к уравнению вида (3.22) нужно обе части (3.23) умножить на нормирующий множитель . Знаквыбирается противоположным знакув (3.23).

В самом деле, пусть уравнения иопределяют одну и ту же прямую. Тогда (см. замечание в 3.2) существует такое число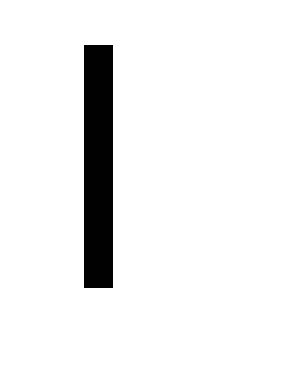, что,,, а.

Из равенства следует, что знакиипротивоположны ().

Пример 4. Найти расстояние от точки 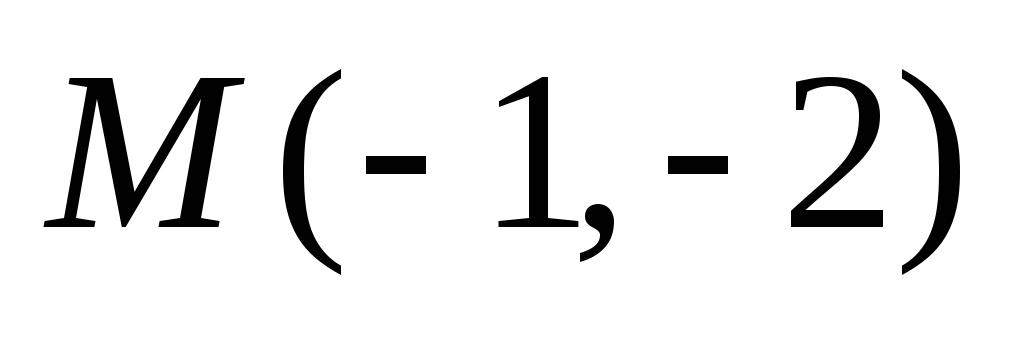до прямой.

Имеем . Нормированное уравнение заданной прямой:

,

.

49