
Лекция 14 Квадратичные формы
|
Определение квадратичной формы. Линейное преобразование неизвестных. Ранг формы. Основная теорема о квадратичных формах. Положительно определенные формы. Критерий Сильвестра. Приведение общего уравнения кривой второго порядка к каноническому виду |
14.1. Приведение квадратичной формы к каноническому виду
Определение 1.Квадратичной формой
от
![]() неизвестных
неизвестных![]() называется сумма вида
называется сумма вида
 ,
(14.1)
,
(14.1)
или развернуто
![]()
![]() .
(14.2)
.
(14.2)
Матрица
![]() ,
называетсяматрицей квадратичной
формы(14.1), а ее ранг – рангом формы
(14.1).
,
называетсяматрицей квадратичной
формы(14.1), а ее ранг – рангом формы
(14.1).
Если ранг формы равен
![]() ,
форма называетсяневырожденной(в
этом случае ранг матрицы
,
форма называетсяневырожденной(в
этом случае ранг матрицы![]() равен
равен![]() и матрица
и матрица![]() невырожденная).
невырожденная).
В (14.2)
![]() ,
,![]() ,
,![]() ,
поэтому коэффициент при слагаемом
,
поэтому коэффициент при слагаемом![]() можно обозначить
можно обозначить![]() ,
т.е. допустить, что
,
т.е. допустить, что![]() .
.
Ввиду последнего равенства
![]() - симметрическая матрица.
- симметрическая матрица.
Запишем квадратичную форму (14.1) в
матричном виде. Пусть
 ,
тогда
,
тогда![]() и
и
![]() .
(14.3)
.
(14.3)
Действительно, по определению умножения матриц имеем
 Далее
находим
Далее
находим

и равенство (14.3) выполняется.
Определение 2.Линейным преобразованием
неизвестных называется такой переход
от системы
![]() неизвестных
неизвестных![]() к системе
к системе![]() неизвестных
неизвестных![]() ,
при котором старые неизвестные выражаются
через новые линейно с некоторыми
коэффициентами:
,
при котором старые неизвестные выражаются
через новые линейно с некоторыми
коэффициентами:
 (14.4)
(14.4)
Линейное преобразование (14.4) однозначно
определяется матрицей из коэффициентов
![]() ,
,![]() .
.
Систему равенств (14.4) можно записать в матричном виде
 .
(14.5)
.
(14.5)
Определение 3.Линейное преобразование
неизвестных с матрицей
![]() называется невырожденным, если
называется невырожденным, если
![]() -невырожденная матрица.
-невырожденная матрица.
Теорема
1.
Пусть
вслед за линейным преобразованием
(14.4) с матрицей
![]() выполняется
линейное преобразование
выполняется
линейное преобразование
![]() с матрицей
с матрицей
![]() ,
,![]() ,
,![]() .
Результирующее преобразование будет
линейным с матрицей
.
Результирующее преобразование будет
линейным с матрицей
![]() .
.
Доказательство. По условию
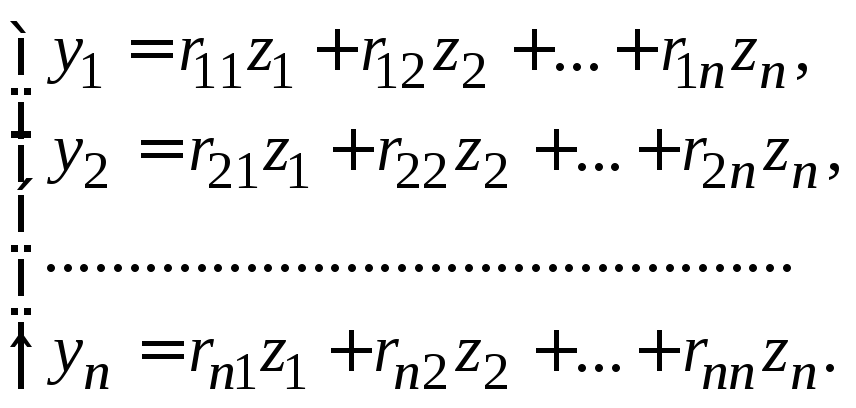 (14.6)
(14.6)
Подставив
в (14.4) выражения для
![]() ,
,![]() ,
из (14.6), получим линейные выражения для
,
из (14.6), получим линейные выражения для
![]() через
через
![]() , т.е. результат последовательного
выполнения двух линейных преобразований
неизвестных является линейным
преобразованием.
, т.е. результат последовательного
выполнения двух линейных преобразований
неизвестных является линейным
преобразованием.
Далее
имеем
![]() ,
,
![]() .
Таким образом, результирующее
преобразование имеет матрицей
.
Таким образом, результирующее
преобразование имеет матрицей![]() .
.
Пример 1. Вслед за линейным преобразованием

выполняется линейное преобразование
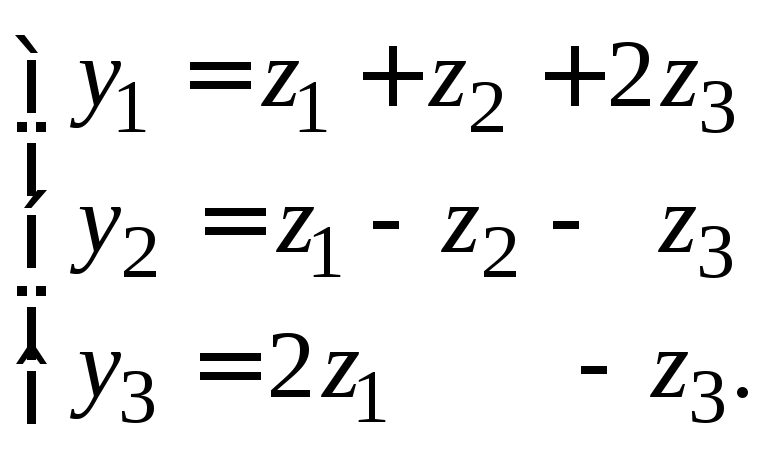
Найти матрицу результирующего
преобразования и выписать выражения
![]() через
через![]() .
.
Решение.Имеем![]() ,
,![]() ,
где
,
где
 ,
, .
.
По теореме 1 матрица результирующего преобразования
 ,
,
и, таким образом,

Утверждение 1. Для любых двух матриц А и В
![]() .
.
Доказательство. Пусть
 ,
, .
.
Обозначим
![]() ,
,![]() ,
,![]() ,
,
![]() .По
определению произведения матриц
.По
определению произведения матриц
![]() .
.
Обозначим
![]() .
По определению транспонированной
матрицы
.
По определению транспонированной
матрицы![]() .
.
Обозначим
![]() .
Элемент
.
Элемент![]() равен сумме произведений элементов
равен сумме произведений элементов
![]() -ой
строки матрицы
-ой
строки матрицы![]() на соответствующие элементы
на соответствующие элементы
![]() -го
столбца
-го
столбца
![]() =
сумме произведений элементов
=
сумме произведений элементов
![]() -го
столбца
-го
столбца
![]() на соответствующие элементы
на соответствующие элементы
![]() -й
строки
-й
строки
![]() ,
и приходим к равенству
,
и приходим к равенству
![]() .
.
Таким
образом,
![]() ,
т.е.
,
т.е.![]() .
.
Теорема
2.
Квадратичная
форма от n
неизвестных с матрицей
![]() после
выполнения линейного преобразования
неизвестных с матрицей
после
выполнения линейного преобразования
неизвестных с матрицей
![]() превращается в квадратичную форму от
новых неизвестных с матрицей
превращается в квадратичную форму от
новых неизвестных с матрицей![]() .
.
Доказательство. Пусть
![]() (14.7)
(14.7)
и
![]() ,
,![]() ,
,![]() .
.
В
соответствии с утверждением 1
![]() .
Подставим
.
Подставим![]() и
и![]() в (14.7):
в (14.7):
 .
.
Матрица
![]() симметрическая, так как
симметрическая, так как
![]()
![]() .
.
Таким
образом,
![]() преобразовалась в квадратичную форму
от неизвестных
преобразовалась в квадратичную форму
от неизвестных
![]() с матрицей
с матрицей
![]() .
.
Докажем два вспомогательных утверждения.
Утверждение 2. Ранг произведения матриц не выше ранга сомножителей.
Доказательство. Достаточно провести доказательство для двух сомножителей.
Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
По определению произведения двух матриц
![]() ,
,
![]() ,
(14.8)
,
(14.8)
![]() ,
,
![]() ,
,
……………………………….
![]() ,
,
или
 ,
,
т.е.
k-й
столбец матрицы
![]() является линейной комбинацией столбцов
матрицы
является линейной комбинацией столбцов
матрицы![]() с коэффициентами
с коэффициентами![]() и система столбцов матрицы
и система столбцов матрицы![]() линейно выражается через систему
столбцов матрицы
линейно выражается через систему
столбцов матрицы![]() ,
следовательно,
,
следовательно,![]() .
.
По
определению произведения матриц
![]() .
.
Аналогично,
фиксируя в (14.8)
![]() и придавая
и придавая![]() значения
значения![]() ,
получаем, что
,
получаем, что
![]() -я
строка
-я
строка
![]() является линейной комбинацией строк
матрицы
является линейной комбинацией строк
матрицы![]() и
и![]() .
.
Утверждение 2 доказано.
Утверждение
3.
Ранг
произведения произвольной матрицы![]() на
невырожденную квадратную
матрицу
на
невырожденную квадратную
матрицу
![]() слева или справа равен рангу
слева или справа равен рангу
![]() .
.
Доказательство.
Пусть
![]() .
В соответствии с утверждением 2
.
В соответствии с утверждением 2
![]() .
.
Умножим
последнее равенство на
![]() справа:
справа:![]() и
опять воспользуемся леммой 2:
и
опять воспользуемся леммой 2:
![]() .
Отсюда
.
Отсюда
![]() .
.
Следствие из теоремы 2. Ранг квадратичной формы не изменяется при выполнении невырожденного линейного преобразования неизвестных.
Доказательство.
Пусть
![]() -
матрица квадратичной формы
-
матрица квадратичной формы![]() ,
,![]() - матрица некоторого невырожденного
линейного преобразования неизвестных,
- матрица некоторого невырожденного
линейного преобразования неизвестных,![]() -
матрица квадратичной формы
-
матрица квадратичной формы![]() после выполнения преобразования
после выполнения преобразования![]() .
.
По
теореме 2
![]() ,
а в силу утверждения 3
,
а в силу утверждения 3
![]() (
(![]() ).
).
Определение 4.Каноническим видом
квадратичной формы![]() называют сумму квадратов неизвестных
с некоторыми коэффициентами.
называют сумму квадратов неизвестных
с некоторыми коэффициентами.
Замечание.Число отличных от нуля коэффициентов в каноническом виде квадратичной формы равно рангу формы.
В самом деле, пусть квадратичная форма
 (14.9)
(14.9)
приведена некоторым невырожденным
линейным преобразованием неизвестных
![]() к каноническому виду
к каноническому виду
![]() ,
(14.10)
,
(14.10)
где
![]() - новые неизвестные.
- новые неизвестные.
Пусть
![]() -
матрица квадратичной формы (14.9),
-
матрица квадратичной формы (14.9),![]() ,
,![]() ,
,![]() ,
,![]() - матрица квадратичной формы (14.10).
- матрица квадратичной формы (14.10).
Матрица
![]() имеет следующий вид:
имеет следующий вид: .
.
Согласно следствию из теоремы 2
![]() .
Утверждение, что
.
Утверждение, что![]() ,
означает, что в матрице
,
означает, что в матрице![]() на диагонали ровно
на диагонали ровно![]() элементов отличны от нуля, тогда в
каноническом виде (14.10) ровно
элементов отличны от нуля, тогда в
каноническом виде (14.10) ровно![]() слагаемых с коэффициентами, отличными
от нуля.
слагаемых с коэффициентами, отличными
от нуля.
Теорема 3 (основная теорема о квадратичных формах). Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду.
Доказательство. Доказательство проведем индукцией по числу неизвестных.
При
![]() имеем
имеем
![]() ,
т.е.
,
т.е.![]() - канонического вида.
- канонического вида.
Пусть
утверждение теоремы справедливо для
![]() :
всякую квадратичную форму от
:
всякую квадратичную форму от
![]() неизвестного можно привести к каноническому
виду некоторым невырожденным линейным
преобразованием и пусть
неизвестного можно привести к каноническому
виду некоторым невырожденным линейным
преобразованием и пусть
 -
-
квадратичная
форма от
![]() неизвестных
неизвестных
![]() .
.
Случай
1.
В форме
![]() присутствует квадрат хотя бы одного
неизвестного. Не ограничивая общности
рассуждений, можно считать, что
присутствует квадрат хотя бы одного
неизвестного. Не ограничивая общности
рассуждений, можно считать, что![]() (в противном случае можно заново
перенумеровать неизвестные). Тогда
(в противном случае можно заново
перенумеровать неизвестные). Тогда![]() можно записать в виде
можно записать в виде
![]() .
(14.11)
.
(14.11)
Действительно,
![]()
![]() ,
,
и
в первое слагаемое в (14.11) вошли все члены
формы
![]() ,
содержащие неизвестное
,
содержащие неизвестное![]() ;
для того, чтобы (14.11) было справедливо,
пришлось добавить, а затем вычесть
несколько слагаемых, не содержащих
;
для того, чтобы (14.11) было справедливо,
пришлось добавить, а затем вычесть
несколько слагаемых, не содержащих![]() ,
поэтому в (14.11)
,
поэтому в (14.11)![]() - некоторая квадратичная форма от
неизвестных
- некоторая квадратичная форма от
неизвестных![]() .
.
От
неизвестных
![]() перейдем к
перейдем к![]() по формулам
по формулам
 (14.12)
(14.12)
или
в матричной записи:
![]() ,
где
,
где
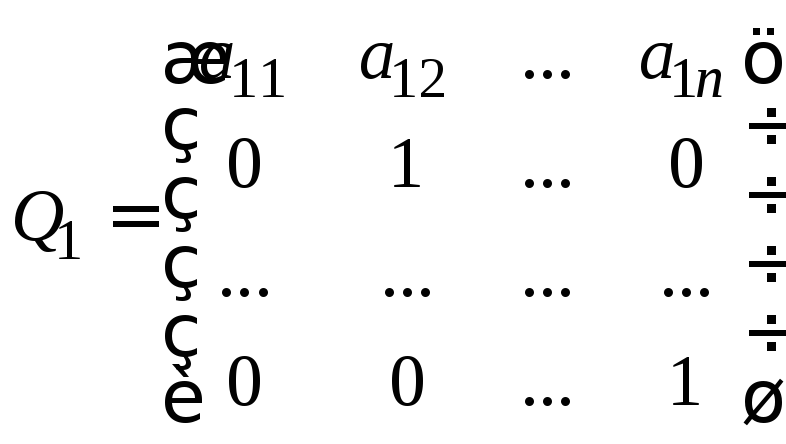 .
.
Матрица
![]() невырожденная, так как
невырожденная, так как![]() ,
следовательно,
,
следовательно,![]() и
и![]() .
.
Невырожденное
линейное преобразование неизвестных
![]() приводит форму
приводит форму![]() к виду
к виду
![]() .
(14.13)
.
(14.13)
Квадратичная
форма
![]() - форма от
- форма от![]() -го
неизвестного и по предположению индукции
найдется невырожденное линейное
преобразование неизвестных
-го
неизвестного и по предположению индукции
найдется невырожденное линейное
преобразование неизвестных![]() ,
приводящее ее к каноническому виду
,
приводящее ее к каноническому виду![]() .
Пусть это преобразование с матрицей
.
Пусть это преобразование с матрицей![]() ,
,![]() :
:

(![]() - невырожденная матрица и
- невырожденная матрица и![]() ).
).
Рассмотрим
теперь линейное преобразование
неизвестных
![]() :
:
 (14.14)
(14.14)
или
в матричной записи
![]() ,
где
,
где
 .
.
Линейное
преобразование (14.14) невырожденное, так
как
![]() и приводит квадратичную форму (14.13) к
виду
и приводит квадратичную форму (14.13) к
виду
![]() (14.15)
(14.15)
Последовательное
выполнение линейных преобразований
(14.12) и (14.14) является линейным преобразованием
и имеет матрицей
![]() (теорема 1). Оно будет невырожденным, так
как
(теорема 1). Оно будет невырожденным, так
как![]() .
Линейное преобразование
.
Линейное преобразование![]() приводит квадратичную форму
приводит квадратичную форму![]() к каноническому виду (14.15).
к каноническому виду (14.15).
Утверждение теоремы в случае 1 доказано.
Случай
2.
Квадратичная форма
![]() не содержит ни одного квадрата неизвестного
(
не содержит ни одного квадрата неизвестного
(![]() ).
).
Совершим
невырожденное линейное преобразование,
приводящее к появлению квадратов
неизвестных. Пусть, например,
![]() :
:
![]() .
(14.16)
.
(14.16)
Положим

или
 .
.
Линейное
преобразование
![]() невырожденное, так как
невырожденное, так как![]() ,
оно приведет квадратичную форму (14.16) к
виду
,
оно приведет квадратичную форму (14.16) к
виду
![]() ,
,
появились
квадраты неизвестных
![]() и
и![]() ,
свели к уже рассмотренному случаю 1.
Теорема 3 полностью доказана.
,
свели к уже рассмотренному случаю 1.
Теорема 3 полностью доказана.
Пример 2. Квадратичную форму
![]()
привести к каноническому виду посредством невырожденного линейного преобразования.
Решение.Соберем все слагаемые,
содержащие неизвестное![]() ,
и дополним их до полного квадрата
,
и дополним их до полного квадрата
![]()
![]()
![]() .
.
(Так как
![]() .)
.)
Положим
 (14.17)
(14.17)
и
от неизвестных
![]() форма
форма![]() примет вид
примет вид![]() .
.
Далее
положим
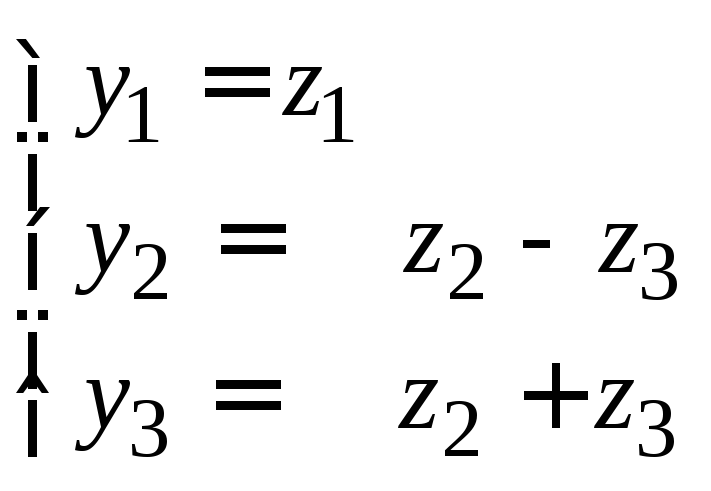 (14.18)
(14.18)
и
от неизвестных
![]() форма
форма![]() примет уже канонический вид
примет уже канонический вид
![]() .
(14.19)
.
(14.19)
Разрешим
равенства (14.17) относительно
![]() :
:

Последовательное
выполнение линейных преобразований
![]() и
и![]() ,
где
,
где
 ,
, ,
,
имеет матрицей
 .
.
Линейное
преобразование неизвестных
![]() приводит
квадратичную форму
приводит
квадратичную форму
![]() к каноническому виду (14.19).
к каноническому виду (14.19).
