
- •Аннотация
- •Оглавление
- •Предисловие
- •ГЛАВА 1. Задачи оптимизации. Основные определения
- •1.1. Задачи оптимизации
- •1.2. Минимум функции одной переменной
- •1.3. Унимодальные функции
- •1.4. Выпуклые функции
- •1.5. Условие Липшица
- •1.6. Классическая минимизация функции одной переменной
- •Вопросы и задания для самоконтроля
- •ГЛАВА 2. Одномерная минимизация функций. Прямые методы
- •2.1. О прямых методах
- •2.2. Метод перебора
- •2.3. Метод поразрядного поиска
- •2.4. Метод дихотомии
- •2.5. Метод золотого сечения
- •2.6. Сравнение методов перебора, дихотомии и золотого сечения
- •2.7. Метод парабол
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 3. Одномерная минимизация. Методы, использующие информацию о производных целевой функции
- •3.1. Метод средней точки
- •3.2. Метод хорд
- •3.3. Метод Ньютона
- •3.4. Возможные модификации метода Ньютона
- •3.5. Методы минимизации многомодальных функций
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 4. Задача минимизации функции многих переменных. Необходимые и достаточные условия безусловного экстремума
- •4.1. Постановка задачи и определения
- •4.2. Свойства выпуклых множеств и выпуклых функций
- •4.3. Необходимые и достаточные условия безусловного экстремума
- •Вопросы и задания для самоконтроля
- •5.1. Выпуклые квадратичные функции
- •5.2. Общие принципы многомерной минимизации
- •5.3. Метод градиентного спуска
- •5.4. Метод наискорейшего спуска
- •5.5. Метод сопряженных направлений
- •5.6. Метод сопряженных градиентов
- •5.7. Метод Ньютона
- •5.8. Квазиньютоновские методы
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 6. Прямые методы безусловной минимизации многомерных задач
- •6.1. Проблема минимизации многомерных задач
- •6.2. Минимизация функций по правильному (регулярному) симплексу
- •6.3. Минимизация функций при помощи нерегулярного симплекса
- •6.4. Метод циклического покоординатного спуска
- •6.5. Метод Хука–Дживса
- •6.6. Методы случайного поиска
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •7.1. Условный экстремум при ограничениях типа равенств
- •7.2. Условный экстремум при ограничениях типа неравенств
- •Вопросы и задания для самопроверки
- •ГЛАВА 8. Линейное программирование
- •8.1. Определения. Примеры задач линейного программирования
- •8.2. Общая и каноническая задачи линейного программирования
- •8.3. Геометрическое истолкование задач линейного программирования
- •8.4. Аналитическое решение задач линейного программирования
- •Вопросы и задания для самоконтроля
- •Литература
□ Из свойства дифференцируемости функции и условия теоремы следует, что
f (xk +α pk ) − f (xk ) = ( f (xk ), |
α pk ) + o(α) =α(( f (xk ), pk ) + o(α) /α) < 0 |
при |
всех |
|||
достаточно малых |
α > 0 , |
т.е. вектор |
pk задает направление убывания функции |
|||
f (x) в точке xk . ■ |
|
|
|
|
|
|
Геометрически |
условие |
теоремы |
( f (xk ), pk ) < 0 означает, что |
вектор |
pk |
|
составляет тупой угол с градиентом f (xk ) . |
|
|
||||
Итак, пусть функция |
f (x) дифференцируема в En . Рассмотрим итерационную |
|||||
процедуру минимизации |
|
|
|
|
|
|
|
xk +1 |
= xk +αk pk , |
k = 0, 1, ... , |
(5.11) |
||
где направление убывания |
pk определяется с учетом информации |
о частных |
||||
производных функции f (x) , а величина шага αk > 0 такова, что |
|
|
||||
|
f (xk +1 ) < f (xk ), |
k = 0, 1, ... |
(5.12) |
|||
Так как функция предполагается дифференцируемой, то в качестве
прекращения итераций можно выбрать условие 
 f (x k )
f (x k )
 <ε .
<ε .
5.3. Метод градиентного спуска
Положим в (5.11) на каждом шаге pk = − f (xk ) . Если f (xk ) ≠ 0 , то условие
( f (xk ), pk ) < 0 , очевидно, выполнено. Следовательно, направление вектора pk
является направлением убывания функции f (x) , причем в малой окрестности точки xk направление pk обеспечивает наискорейшее убывание этой функции.
Поэтому можно найти такое αk > 0 , что будет выполняться условие (5.12).
Алгоритм метода градиентного спуска следующий.
Шаг 1. Задать параметр точности ε >0 , начальный шаг α > 0 , выбрать x En и
вычислить |
f (x) . Перейти к шагу 2. |
|
|
|
|
|
|
|||
Шаг 2. |
Вычислить f (x) и проверить условие достижения точности |
|
|
|
f (x) |
|
|
|
<ε . |
|
|
|
|
|
|||||||
Если оно выполнено, |
то вычисления завершить, полагая x = x , f = f (x) . Иначе |
|||||||||
перейти к шагу 3. |
|
|
|
|
|
|
|
|
|
|
Шаг 3. Найти |
y = x −α f (x) и f ( y) . Если f ( y) < f (x) , то |
|
положить |
|||||||
x = y , f (x) = f ( y) и перейти к шагу 2, иначе − к шагу 4.
Шаг 4. Положить α =α / 2 и перейти к шагу 3.
79

Необходимо отметить, что вблизи стационарной точки функции f (x) величина
|
f (x) |
|
|
|
становится |
малой. Это часто приводит к замедлению сходимости |
|
|
|
||||
последовательности |
{xk }. Поэтому в основной формуле (5.11) иногда полагают |
|||||
pk = − f (xk ) /
 f (xk )
f (xk )
 , используя вместо антиградиента вектор единичной длины в этом же направлении.
, используя вместо антиградиента вектор единичной длины в этом же направлении.
Сформулируем теоретическое обоснование сходимости градиентного метода с
постоянным шагом αk = α , |
т.е. xk +1 = xk −α f (xk ) |
и оценку скорости сходимости |
|||||
при минимизации выпуклой квадратичной функции f (x) = |
1 |
( Ax, x) + (b, x) + c . |
|||||
2 |
|||||||
|
|
|
|
|
|
||
Теорема. Пусть симметрическая матрица A |
квадратичной |
функции f (x) |
|||||
положительно определена, |
l и L |
− ее наименьшее и наибольшее собственные |
|||||
значения (0 < l ≤ L) . Тогда |
при |
любых α (0, |
2 / L) и |
|
x0 En |
итерационная |
|
последовательность xk +1 |
= xk −α f (xk ) сходится к единственной точке глобального |
||||||||
минимума x функции |
f (x) линейно (т.е. со скоростью геометрической |
||||||||
прогрессии), а именно |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ρ (xk , x ) ≤ qk ρ (x0 , x ) , |
где q = max{ |
1−α l |
|
, |
|
1−αL |
|
}. |
положительно определена, то функция f (x) сильно |
|
|
|
|
|||||||
□ Так как матрица |
A |
||||||||
выпукла. Следовательно, точка x существует и единственна. Градиент f (x ) в
этой точке обращается в нуль, поэтому f (xk ) = Axk +b = Axk +b − Ax −b =
A(xk − x ) .
Оценим норму разности

 xk − x
xk − x 
 =
= 
 xk −1 −α f (xk −1 ) − x
xk −1 −α f (xk −1 ) − x 
 =
= 
 xk −1 − x −α A(xk −1 − x )
xk −1 − x −α A(xk −1 − x )
 =
= 
 (E −α A)(xk −1 − x )
(E −α A)(xk −1 − x )
 .
.
Последняя величина может быть оценена сверху
|
|
|
|
|
xk − x |
≤ |
|
|
|
E −α A |
|
|
|
|
xk −1 − x |
|
≤ q |
xk −1 − x |
≤ qk |
x0 − x |
. |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Здесь величина q |
− оценка нормы матрицы через величину ее собственных |
|||||||||||||||||||||||||||||
значений: |
|
|
|
E −α A |
|
|
|
≤ q = max{ |
1−αl |
|
, |
|
1−αL |
|
}. |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
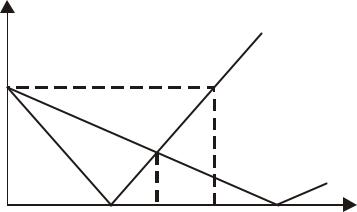
Зависимость q(α) |
представлена на рис. 5.2, из которого видно, что при |
|||||||||||||||||||||||||||||
α (0;2 / L) |
|
величина q <1. ■ |
||||||||||||||||||||||||||||
80
q
1
q(α)
0 1/L α* 2/L 1/l α
Рис. 5.2. Зависимость оценки знаменателя геометрической прогрессии от величины шага α градиентного метода
Из формулы |
для |
величины |
q |
следует, что она принимает минимальное |
||||
значение q = |
L −l |
при |
α |
=α = |
|
2 |
(так как l < L , то 1 −α l = −(1 −α L) ). Поэтому |
|
L +l |
L +l |
|||||||
|
|
|
|
|
||||
от соотношения между |
L |
и l существенно зависит число итераций градиентного |
||||||
метода при минимизации выпуклой квадратичной функции. Рассмотрим это на примере квадратичной функции двух переменных.
При L =l > 0 точка минимума f (x) находится за один шаг. |
|
|
|
||
Пример. 5.3. Решить задачу f (x) = x2 |
+ x2 → min |
градиентным методом из |
|||
1 |
2 |
|
|
|
|
начальной точки x0 = (1, 1)T , положив α = α . |
|
|
|
|
|
□ В данном случае матрица квадратичной функции |
2 |
0 |
|
, отсюда l = L = 2 . |
|
A = |
|
|
|||
|
|
|
2 |
|
|
|
|
0 |
|
|
|
Поэтому α = |
2 |
= |
1 |
и x1 = x0 |
− |
1 |
f (x0 ) = (0, 0)T . Следовательно, |
x1 = x . ■ |
|
L + l |
2 |
2 |
|||||||
|
|
|
|
|
|
||||
При l = L |
линии |
уровня |
целевой функции f (x) − это концентрические |
||||||
окружности, поэтому направление антиградиента указывает на их центр, т.е. на точку глобального минимума f (x) .
Если L >> l > 0 , то линиями уровня являются эллипсы, полуоси которых сильно различаются. Поэтому направление антиградиента в некоторой точке может сильно отличаться от направления к точке глобального минимума.
Пример. 5.4. Из начальной точки x0 = (1, 1)T выполнить несколько итераций поиска точки минимума функции f (x) = x12 +100x22 градиентным методом, полагая
α = α .
81
□ Собственные значения матрицы A этой квадратичной функции: l = 2, L = 200 .
Линиями |
уровня |
f (x) являются эллипсы, |
|
|
сильно |
|
вытянутые вдоль |
оси Ox1 . |
||||||||||||||
Поэтому в точке x0 направление вектора − f (x0 ) = (−2, − 200)T |
сильно отличается |
|||||||||||||||||||||
от направления к точке глобального |
минимума |
x − x0 |
= (−1, |
−1)T . Положив в |
||||||||||||||||||
формуле |
xk +1 = xk |
−α f (xk ) величину |
α=α |
= |
|
2 |
|
= |
1 |
|
, |
получим |
с учетом |
|||||||||
L + l |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
101 |
|
|
|
|
||||||
выражения для градиента f (x) = (2x , 200 x |
2 |
)T |
закон изменения координат точек |
|||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
минимизирующей последовательности: |
xk +1 |
= |
|
99 |
|
xk , |
xk +1 = − |
99 |
|
xk . Отсюда видно, |
||||||||||||
101 |
|
|
||||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
2 |
|
|
101 |
2 |
|
|||||||
что последовательность {xk } сходится к точке глобального экстремума медленно и траектория сходимости имеет ярко выраженный зигзагообразный характер. ■
В курсах линейной алгебры и численных методов для симметрической положительно определенной матрицы вводится число обусловленности, которое равно μ = L / l − отношению наибольшего и наименьшего собственных значений матрицы. В задаче минимизации сильно выпуклой функции f (x) эта величина для матрицы ее вторых производных (гессиана) характеризует степень вытянутости линий уровня f (x) = C . Если μ велико, то линии уровня сильно вытянуты и
говорят, что функция имеет овражный характер, т.е. резко меняется по одним направлениям и слабо − по другим. В этих случаях задачу минимизации называют плохо обусловленной. Если же число μ близко к единице, то линии уровня близки к окружностям и задача минимизации является хорошо обусловленной.
Вычисление градиента на каждом шаге, позволяющее каждый раз двигаться в направлении все более быстрого убывания целевой функции, может в то же время замедлить вычислительный процесс. Дело в том, что подсчет градиента − обычно гораздо более сложная операция, чем подсчет самой функции. Поэтому часто пользуются модификацией градиентного метода, получившей название метода наискорейшего спуска.
Согласно этому методу после вычисления в начальной точке градиента функции делают в направлении антиградиента не маленький шаг, а передвигаются до тех пор, пока функция убывает. Достигнув точки минимума на выбранном направлении, снова вычисляют градиент функции и повторяют описанную
82
