SemTE / Sem1

СЕМИНАР 1 Статистика электронов и дырок

Единицы измерения в системе СИ:

Основные: м кг с А К

Производные: Дж Вт Кл В Ом Ф

Дж = м*кг/с = A*B*c = 1 Вт*с

1 Вт = 1 Дж/с 1 эВ = 1.6*10^-19 Дж

φ_t = k*T/e = 25.8 мВ (при 300 К) = 4.14*10^-21 Дж

1 мкм = 10^-4 см = 10^-6 м 1 нм = 10^-7 см = 10^-9 м

Приближенные вычисления:

- ln 10 = 2.3 ln 10¹⁵ = 15*ln 10 = 15*2.3 = 34.5

- exp 1 = 2.718, exp 10 = 2.2*10⁴, exp 20 = 4.85*10⁸

Физические постоянные:

h = 6.62*10^-34 Дж*с k = 1.38*10^-23 Дж/К e = 1.6*10^-19 Кл m = 9.1*10^-31 кг

ε₀ = 8.86*10^-14 Ф/см εε₀ = 1.1 пФ/см (для Si) ε_dε₀ = 0.4 пФ/см (для SiO₂)

Свойства полупроводников

п/п	Eg, эВ	ni, см-3	Подвижность n/p см2/(В*с)	ε
Si	1.12	1.5*1010	1500 / 600	11.9
Ge	0.66	2.5*1013	3900 / 1900	16
GaAs	1.43	1.8*106	8500 / 400	10.9

Марка подложки	Материал	Проводимость	Удельное сопротивление при T=300 К, ρ [Ом*см]	Концентрация примеси при T=300 К, N [см-3]
КДБ-10	Si	дырочная	10	Na = 1015 см-3
КЭФ-4.5	Si	электронная	4.5	Nd = 1015 см-3

Теоретические сведения

Зонная диаграмма полупроводника

Функция распределения Ферми-Дирака

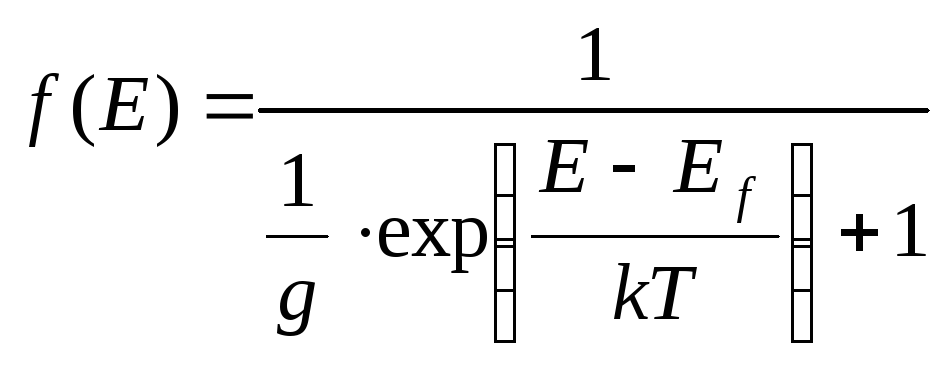
g – фактор вырождения примесного уровня;

g =1 для собственного полупроводника,

g = 2 для донорного примесного уровня (электрон на одном уровне может иметь два значения спина)

В полупроводнике выделяют следующие концентрации:

- N_d – полная концентрация донорной примеси, N_d⁺ - концентрация ионизированных доноров

- N_a – полная концентрация акцепторной примеси, N_а⁺ - концентрация ионизированных акцепторов

- n – концентрация электронов,

- р – концентрация дырок

Справедливо уравнение электронейтральности и формулы для концентраций:

n₀ + N_a^- = p₀ + N_d⁺

, = 2.83*10¹⁹ см^-3 (для Si, 300 К)

, = 1.02*10¹⁹ см^-3 (для Si, 300 К)

m_c = 1.08*m, m_v = 0.56*m

- Закон действия масс для невырожденных п/п

ЗАДАЧА 1

Для собственного полупроводника найти вероятность заполнения электроном уровня на дне Ес при T=0 и 300 К. Считать что при 300 К уровень Ферми (E_f) расположен по середине Е_g (E-E_f = E_g/2)

Решение:

Используем функцию распределения Ферми-Дирака

При расчете можно считать, что энергия выражается в вольтах, а вместо kT использовать φ_t = 25.8 мВ

= 1.86*10^-10

ЗАДАЧА 2

Вычислить положение уровня Ферми (E_f) в собственном Si при T=300K

Решение: В собственном полупроводнике нет примесей. Из уравнения электронейтральности следует, что n = p. Используя формулы для концентраций:

ЗАДАЧА 3

Найти концентрацию электронов и дырок в кремнии при Т=300К, если концентрация донорной примеси N_d = 10¹⁶ cм^-3, N_а = 0. Считать примесь полностью ионизованной.

Решение: Уравнение электронейтральности при полной ионизации примеси имеет вид:

n₀ + N_a = p₀ + N_d

Из закона действия масс: p₀ = n_i²/n₀

Составляем квадратное уравнение: n₀²-(N_d-N_a)*n₀-n_i²=0

Решение: =10¹⁶ см^-3 p₀ = 2.25*10⁴ см^-3

МОЖНО СЧИТАТЬ, ЧТО ПРИ N_а = 0: n₀ = N_d, p₀ = n_i²/N_d

ЗАДАЧА 4

Рассчитать концентрацию электронов и дырок в кремнии с концентрацией примеси N_а = 10¹⁶ см^-3, N_d = 3*10¹⁵ см^-3, Т=300 К

Решение:

=7*10¹⁵ см^-3

n₀ = n_i²/N_a = 3.2*10⁴ см^-3

МОЖНО СЧИТАТЬ ЧТО:

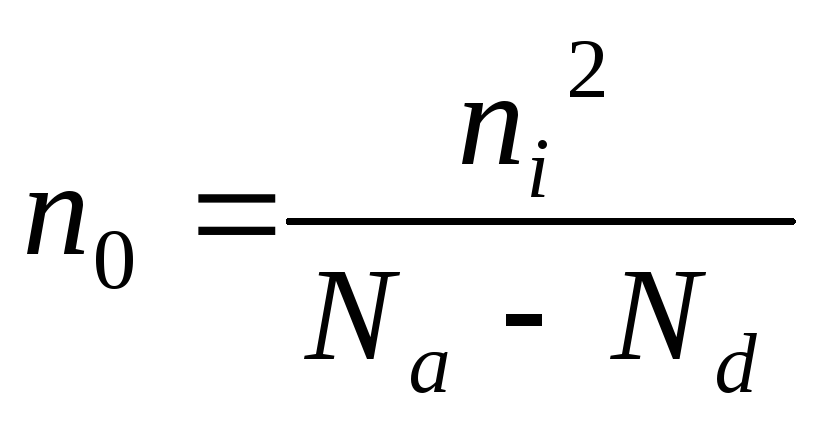
ЗАДАЧА 5

Образец кремния n-типа находится в состоянии термодинамического равновесия при T=300K. Параметры образца:

• ρ = 5 Ом*см

• μ_n = 1600 μ_p = 600 [см²/(В*с)]

• n_i = 1.4*10¹⁰ см^-3, N_c = 10¹⁹ см^-3

• E_c - E_d = 0.05 эВ

Найти:

1. Концентрацию электронов и дырок

2. Положение уровня Ферми

3. Вероятность того, что донорный уровень занят или свободен

Решение:

1. ρ = 1/σ

2. σ = e(μ_n n + μ_p p)

3. n*p = n_i²

4. σ = e( μ_n n + μ_p n_i²/n )

=7.81*10¹⁴ см^-3

р = 2.5*10⁵ см^-3

2. , находим E_c-E_f = 0.244 эВ

3. Так как E_c - E_d = 0.05 эВ, то E_d - E_f = 0.194 эВ и вероятность заполнения донорного уровня определяется функцией распределения Ферми-Дирака

8.5*10^-4

ЗАДАЧА 6

Найти удельное сопротивление (ρ) собственного Si при 300 К.

Решение:

ρ = 1/σ

σ = e(μ_n n + μ_p p) = e μ_p n_i (B+1)

B=μ_n / μ_p =2.5

ρ = 1.2 *10⁶ Ом*см