
sss / 15_Трунова_06
.docxУпражнение 1
Прямая L
задана т
 и направляющим вектором
и направляющим вектором
 .
.
1.Записать каноническое уравнение прямой (см формулу (5)) и сделать его заголовком графика.
2.Теперь
входными параметрами являются координаты
направляющего вектора
 и координаты точки прямой
и координаты точки прямой
 =
(X0, Y0).
Выразить из канонического уравнения
y, как функцию от x.
Используя функцию plot(),
построить прямую L,
сплошную, фиолетового цвета, толщины
2. Значение абсцисс точек прямой –
массив, состоящий из двух точек -6 и 9.
Отметить на прямой точку
=
(X0, Y0).
Выразить из канонического уравнения
y, как функцию от x.
Используя функцию plot(),
построить прямую L,
сплошную, фиолетового цвета, толщины
2. Значение абсцисс точек прямой –
массив, состоящий из двух точек -6 и 9.
Отметить на прямой точку
 круговым маркером черного цвета, толщины
3. Подписать точку. Провести с помощью
функции line( ) оси координат черного
цвета.
круговым маркером черного цвета, толщины
3. Подписать точку. Провести с помощью
функции line( ) оси координат черного
цвета.
3.
Построить направляющий вектор
 ,
берущим начало
,
берущим начало
а) из начала координат
б) из точки, в которой прямая L пересекает ось абсцисс.
q=[3;-1];%определение вектора
M=[1;2]%Задание точки
M =
1
2
x=-6:9;%формирование диапазона абсцисс
y=(q(2)*(x-M(1))+q(1)*M(2))/q(1)% вычисление ординат
y =
Columns 1 through 8
4.3333 4.0000 3.6667 3.3333 3.0000 2.6667 2.3333 2.0000
Columns 9 through 16
1.6667 1.3333 1.0000 0.6667 0.3333 0 -0.3333 -0.6667
plot(x,y,'m-','linewidth',2);grid% построение графика прямой линии
hold on %Включение режима добавления графиков
plot(M(1),M(2),'ko','linewidth',3)%визуализация заданной точки круговым маркером
text(0.5,2.2,'M_{0}(x_{0},y_{0})') % ее обозначение
line([-6 0;10 0],[0 -6;0 6],'Color','black')% вывод координатных осей
xlabel('X'), ylabel('Y')% обозначение осей
title('(x-1)/3=(y-2)/(-1)') % заголовок
line([0,3,3;3,2.8,2.7],[0,-1,-1;-1,-0.6,-1.1],'color','black','linewidth',2)%визуализация направляющего вектора, выходящего из начала координат
line([7,10,10;10,9.7,9.5],[0,-1,-1;-1,-0.7,-1.1],'color','black','linewidth',2)%визуализация направляющего вектора, выходящего из точки, в которой прямая пересекает ось абсцисс
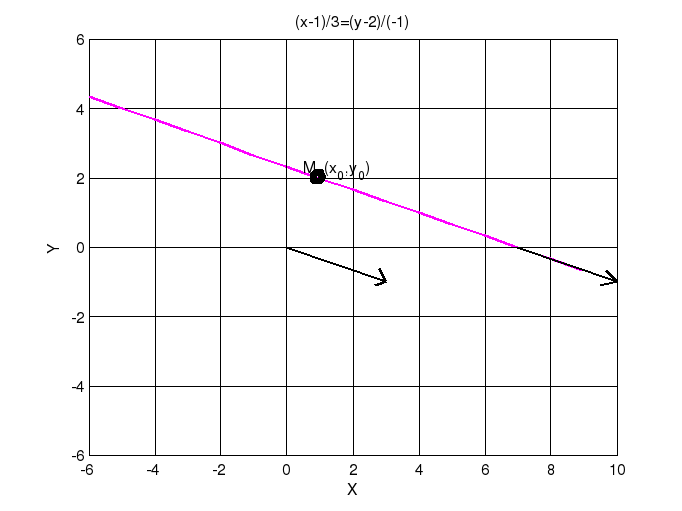
Рисунок
1
Упражнение 2
1. Прямая
L1 задана двумя точками
 и
и
 .
.
Определиться с входными данными.
Выразить из канонического уравнения y, как функцию от x.
Используя функцию plot(), построить прямую L1.
Отметить
и подписать на прямой точки
 и
и

Провести с помощью функции line( ) оси координат черного цвета.
Построить
направляющий вектор
 ,
берущим начало
,
берущим начало
а) из начала координат
б) из точки, в которой прямая L1 пересекает ось абсцисс.
2. Используя
готовую программу, сделать все тоже
самое для прямой L2,
проходящую через точки
 и
и
 .
.
1.
M1=[1;2];%задание точки
M2=[-1;0];%задание точки
q=[M2(1)-M1(1);M2(2)-M1(2)]%определение вектора
q =
-2
-2
x=-6:6;%определение диапазона абсцисс
y=(q(2)*(x-M1(1))+q(1)*M1(2))/q(1)% вычисление ординат
y =
-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
plot(x,y,'r-','linewidth',3)%построение графика прямой
grid on%показ сетки
hold on%включение режима добавления графиков
plot(M1(1),M1(2),'bo','linewidth',3)%визуализация заданной точки круговым маркером
text(1,2.3,'M_{1}(1,2)') % ее обозначение
plot(M2(1),M2(2),'bo','linewidth',3)%визуализация заданной точки круговым маркером
text(-1,0.3,'M_{1}(1,2)') % ее обозначение
line([-6 0;6 0],[0 -6;0 8],'color','black')%вывод координатных осей
xlabel('X'), ylabel('Y')% обозначение осей
line([0,-2,-2;-2,-1.7,-1.3],[0,-2,-2;-2,-1.3,-1.9],'color','green','linewidth',2)%визуализация направляющего вектора, выходящего из начала координат
line([-1,-3,-3;-3,-2.7,-2.3],[0,-2,-2;-2,-1.3,-1.9],'color','green','linewidth',2) %визуализация направляющего вектора, выходящего из точки, в которой прямая пересекает ось абсцисс

Рисунок 2
2.
M1=[2;1];%задание точки
M2=[0;-1];%задание точки
q=[M2(1)-M1(1);M2(2)-M1(2)]%определение вектора
q =
-2
-2
y=(q(2)*(x-M1(1))+q(1)*M1(2))/q(1)% вычисление ординат
y =
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5
x=-6:6;%определение диапазона абсцисс
plot(x,y,'r-','linewidth',3)%построение графика прямой
grid on%показ сетки
hold on%включение режима добавления графиков
line([-6 0;6 0],[0 -6;0 8],'color','black')%вывод координатных осей
line([-8 0;6 0],[0 -6;0 8],'color','black')%вывод координатных осей
line([-6 0;6 0],[0 -8;0 8],'color','black')%вывод координатных осей
plot(M1(1),M1(2),'bo','linewidth',3)%визуализация заданной точки круговым маркером
text(2,2,'M_{1}(2,1)') % ее обозначение
plot(M2(1),M2(2),'bo','linewidth',3)%визуализация заданной точки круговым маркером
text(-0.3,-0.3,'M_{2}(0,-1)') % ее обозначение
line([0,-2,-2;-2,-1.7,-1.3],[0,-2,-2;-2,-1.3,-1.9],'color','green','linewidth',2)
line([1,-1,-1;-1,-0.7,-0.3],[0,-2,-2;-2,-1.3,-1.9],'color','green','linewidth',2)

Рисунок 3
Упражнение 3
Построить
прямую, заданную параметрическим
уравнением
 .
Найти ее направляющий вектор
.
Найти ее направляющий вектор
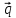 ,
найти нормальный вектор
,
найти нормальный вектор
 .
Изобразить данные векторы исходящими
из начала координат и из какой-нибудь
точки, лежащей на прямой.
.
Изобразить данные векторы исходящими
из начала координат и из какой-нибудь
точки, лежащей на прямой.
M=[-1;3];%задание точки
q=[5;-2];%направляющий вектор
x=-10:10;%определение диапазона абсцисс
y=(q(2)*(x-M(1))+q(1)*M(2))/q(1)% вычисление ординат
plot(x,y,'r-','linewidth',3)%построение графика прямой
grid on%показ сетки
grid on%показ сетки
hold on%включение режима добавления графиков
line([-10 0;10 0],[0 -10;0 7],'color','black')%вывод координатных осей
line([-10 0;10 0],[0 -10;0 8],'color','black')%вывод координатных осей
line([0,5,5;5,4.5,4.2],[0,-2,-2;-2,-1.3,-2.1],'color','green','linewidth',2)%визуализация направляющего вектора, выходящего из начала координат
line([4,9,9;9,8.4,8.2],[1,-1,-1;-1,-0.3,-0.8],'color','green','linewidth',2)%визуализация направляющего вектора
line([0,2,2;2,1.3,1.9],[0,5,5;5,4.3,4],'color','black','linewidth',2)%визуализация нормального вектора, выходящего из начала координат
line([4,6,6;6,5.3,6],[1,6,6;6,5.3,5],'color','black','linewidth',2)%визуализация нормального вектора
Рисунок
4
