Лекции Ржавинской / Глава_04

Лекция 4

Плоскость и прямая в пространстве

Понятие уравнения поверхности. Различные виды уравнения плоскости. Угол между двумя плоскостями. Расстояние от точки до плоскости. Прямая линия в пространстве, способы ее задания. Угол между двумя прямыми в пространстве и между прямой и плоскостью.

4.1. Понятие уравнения поверхности

Пусть в пространстве задана декартова система координат и произвольная поверхность . Рассмотрим уравнение

. (4.1)

Определение 1. Уравнение (4.1) называется уравнением поверхности относительно заданной системы координат, если ему удовлетворяют координаты , и любой точки поверхности и не удовлетворяют координаты ни одной точки, не принадлежащей поверхности .

Таким образом, поверхность – геометрическое место точек, координаты которых удовлетворяют (4.1).

Если (4.1) является уравнением поверхности , то будем говорить, что уравнение (4.1) определяет поверхность .

Определение 2. Поверхность называется алгебраической, если в некоторой декартовой системе координат определяется уравнением (4.1), в котором – алгебраический полином (сумма конечного числа слагаемых вида , – целые, – некоторая постоянная).

Если при этом – алгебраический полином порядка , поверхность называется алгебраической поверхностью порядка .

Уравнение сферы с центром в точке и радиусом имеет вид

,

поэтому сфера – алгебраическая поверхность 2-го порядка.

Определение 3. Всякая неалгебраическая поверхность называется трансцендентной.

Теорема 1. Если поверхность в некоторой декартовой системе координат определяется алгебраическим уравнением порядка , то и в любой другой декартовой системе координат определяется алгебраическим уравнением того же порядка .

(Приводится без доказательства).

4.2. Уравнение плоскости в общем виде

Теорема 2. Пусть - произвольная декартова система координат. Всякое уравнение вида

, (4.2)

где – действительные числа, причем , и не равны нулю одновременно, определяет относительно плоскость.

Доказательство. Пусть – решение (4.2).

Хотя бы одно такое решение существует. В самом деле, так как , и не равны нулю одновременно, то пусть для определенности . Положим , и получим , и тройка чисел удовлетворяет (4.2), т.е. является решением этого уравнения. Тогда выполняется тождество

. (4.3)

Пусть – другое решение уравнения (4.2), тогда справедливо еще одно тождество:

. (4.4)

Вычтем из (4.4) почленно (4.3) и получим

. (4.5)

Рассмотрим вектор и две точки и , .

Равенство (4.5) – условие того, что . Таким образом, если - решение уравнения (4.2), то точка является концом вектора , перпендикулярного , т.е. принадлежит плоскости , проходящей через точку и перпендикулярной (рис. 4.1).

Обратно. Пусть , проходящей через точку и перпендикулярной вектору . Тогда и выполняется равенство (4.5), а значит, с учетом (4.3) справедливо (4.4) и - решение уравнения (4.2).

Таким образом, плоскость состоит из тех и только тех точек, координаты которых удовлетворяют (4.2), следовательно, уравнение (4.2) – уравнение плоскости .

Уравнение (4.2) называется общим уравнением плоскости, вектор – нормальным вектором плоскости.

Пример 1. Составить уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.

Пусть , и – три точки, не лежащие на одной прямой. Тогда через них можно провести плоскость и притом только одну. Пусть это плоскость (рис. 4.2).

Имеем векторы , и компланарны смешанное произведение трех векторов обращается в нуль: или в координатной форме

. (4.6)

Уравнение (4.6) – уравнение плоскости, проходящей через три точки, не лежащие на одной прямой.

Пример 2. Составить уравнение плоскости, пересекающей оси координат в точках , и ( (рис. 4.3).

Воспользуемся уравнением (4.6), считая , , :

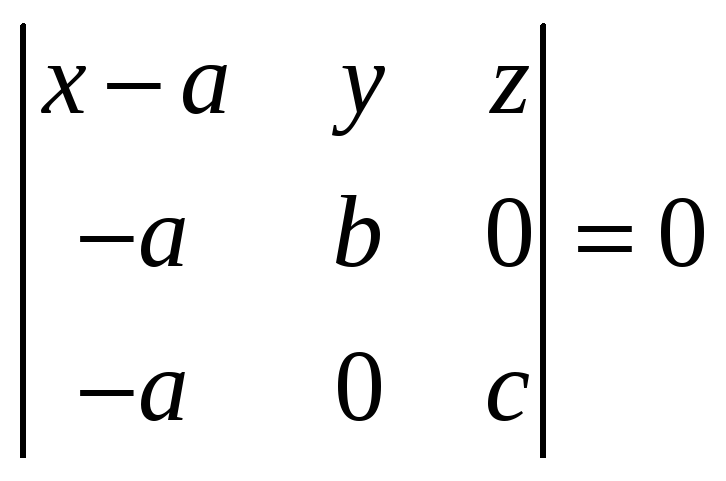. (4.7)

Раскроем определитель в (4.7): , или , или

(4.8)

Уравнение (4.8) называется уравнением плоскости в отрезках ( - «отрезки» с учетом знака, отсекаемые плоскостью (4.8) на осях , и соответственно).

Рассмотрим задачу определения угла между двумя плоскостями. Заметим, что две плоскости, пересекаясь, образуют два двугранных угла, составляющих в сумме (рис. 4.4).

Любой из этих углов будем называть углом между плоскостями и и обозначать в дальнейшем .

Пусть плоскости и заданы своими общими уравнениями

: ,

: .

Тогда известны координаты нормальных векторов и . Один из двугранных углов между плоскостями и равен углу между нормальными векторами и (они равны как углы с соответственно перпендикулярными сторонами (рис.4.5)).

Отсюда следует справедливость равенства

. (4.9)

В самом деле,

,

и равенство (4.9) верно.

Отметим частные случаи:

1) и коллинеарны . (4.10)

Равенство (4.10) – условие параллельности двух плоскостей.

(Условие совпадения доказывается аналогично тому, как доказывается условие совпадения двух прямых, заданных общими уравнениями).

2) (числитель дроби (4.9) равен нулю).

4.3. Нормированное уравнение плоскости. Расстояние от точки до плоскости

Пусть - декартова система координат, - произвольная плоскость. Проведем через точку прямую , точку пересечения обозначим . Возьмем вектор такой, что: приложен к точке О, , направление совпадает с направлением вектора .

Если , направление выберем произвольно (рис. 4.6).

Пусть - углы наклона вектора к осям , и соответственно. Тогда . Обозначим . Имеем

; (4.11) ; (4.12)

. (4.13)

Из (4.11), (4.12) и (4.13) получим:

или

. (4.14)

Уравнение (4.14) называется нормированным уравнением плоскости (в 4(.14) - расстояние от начала координат до плоскости, - углы наклона вектора к осям , и соответственно).

Приведем без доказательства следующее утверждение.

Теорема 3. Расстояние от точки до плоскости равно абсолютной величине результата подстановки координат этой точки в левую часть нормированного уравнения плоскости :

. (4.15)

Замечание. Для того чтобы от общего уравнения плоскости

(4.16)

перейти к нормированному уравнению (4.14), нужно обе части (4.16) умножить на нормирующий множитель ; знак выбирается противоположным знаку в (4.16).

Действительно, уравнения (4.16) и (4.14) определяют одну и ту же плоскость в том и только в том случае, когда все четыре коэффициента пропорциональны, т.е. найдется такое , что , , , .

Из первых трех равенств получим

и .

Из равенства следует, что (так как ), следовательно, и разных знаков.

Пример 3. Найти расстояние от точки до плоскости .

Найдем нормирующий множитель . Нормированное уравнение плоскости :

,

.

4.4. Прямая линия в пространстве

Определение 4. Пусть - произвольная прямая, любой вектор , такой, что параллелен , называется направляющим вектором прямой .

Пусть - произвольная декартова система координат, - произвольная прямая, , – направляющий вектор прямой . Этими условиями полностью определяется положение прямой в пространстве.

коллинеарен

. (4.17)

Уравнения (4.17) называются каноническими уравнениями прямой , проходящей через точку и имеющей в качестве направляющего вектор .

Обозначим в (4.17) общее отношение через , тогда

(4.18)

Так как , то хотя бы одно из чисел , , либо отлично от нуля. Пусть для определенности . Тогда при число пробегает всю ось и , и, таким образом, .

Соотношения (4.18) при называются параметрическими уравнениями прямой , проходящей через точку и имеющей в качестве направляющего вектор .

Замечание. Линию в пространстве естественно рассматривать как пересечение двух поверхностей, т.е. как совокупность точек, находящихся одновременно на двух поверхностях.

Если и - уравнения двух поверхностей, пересечением которых является линия , то система уравнений

(4.19)

определяет линию .

Пусть : и : , не параллельна и не совпадает с ней. Тогда система уравнений

(4.20)

определяет линию пересечения и , т.е. прямую.

Таким образом, система (4.20) – задание прямой как линии пересечения двух плоскостей и .

4.5. Угол между двумя прямыми в пространстве и между прямой и плоскостью

Определение 5. Углом между прямыми и называется любой из двух углов, образуемых двумя прямыми и , соответственно параллельными данным и проходящими через одну точку (рис. 4.7).

Пусть : , : .

Тогда ,

в частности .

Отметим еще один частный случай:

и коллинеарны .

О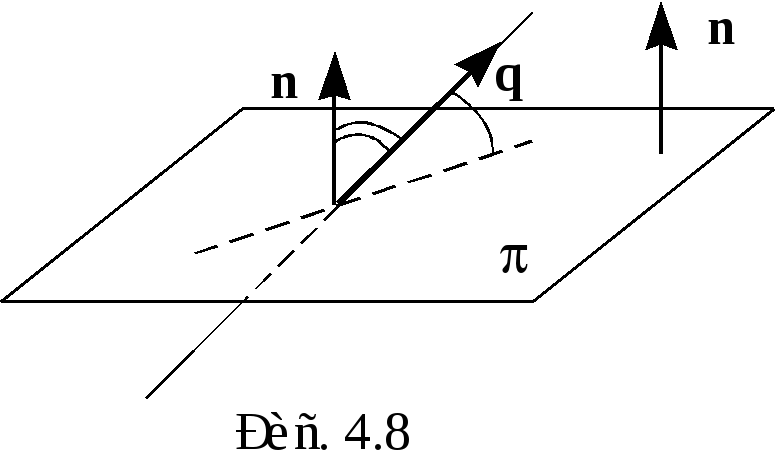пределение 6. Углом между прямой и плоскостью называется острый угол между прямой и ее проекцией на плоскость (рис. 4.8).

Пусть - произвольная плоскость, - произвольная прямая, не перпендикулярная ,

:,

: .

Из определения 6 Поэтому

.