§ 4. Обобщающие примеры по системам линейных неоднородных уравнений 1-го порядка с постоянными коэффициентами.

Набор обобщающих Примеров, представленных ниже, предназначен оказать максимальную помощь студентам, испытывающим трудности при изучении темы: Системы линейных неоднородных уравнений 1-го порядка с постоянными коэффициентами.

☺ ☻ ☺

Пример 13–01: Решить систему нелинейных уравнений: (1.1)

Решение:

1). Найдем характеристические корни соответствующей однородной системы (т.е. без функции ):== 0, откуда получаем:=–3; =2.В этом случае общее решение однородной системы будем искать в виде:

=+, (2.1)

где =∙e^–3t=∙,=∙e^2t=∙, (3.1)

2). Для определения векторов ,составим систему уравнений:

(4.1)

Для корня =–3 система (4.1) имеет решение=; для=2:=.

3). С учетом полученных векторов ,запишем общее решение однородной системы дифференциальных уравнений:=∙∙+∙∙, (5.1)

4). Так как функция: –многочлен 1-й степени и образующее числоне совпадает с характеристическими корнями:и, то частное решение заданной системы будем искать в виде:=, ее производные:=. (6.1)

Подставляя (5.1) в систему (1.1), получаем тождества: (7.1)

Приравнивая коэффициенты при степенях и, получаем систему алгебраических уравнений:

1) при :2) при:→=–,=–,=–,=–. (8.1)

5). Запишем общее решение заданной неоднородной системы:

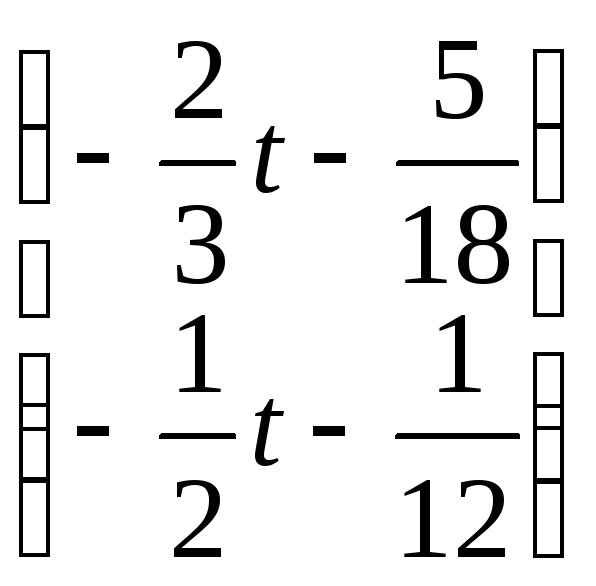=+=∙∙+∙∙+. (9.1)

Ответ: общее решение системы: =∙∙+∙∙+.

Пример 13–02: Решить систему нелинейных уравнений: (1.2)

Решение:

При решении данного Примера воспользуемся теоремой о «суперпозиции» применения функций правой части и запишем две системы, эквивалентные данной, т.е. позволяющие получить общее решение исходной системы:

1a:→ число:,1b:→ число:.

1). Найдем характеристические корни соответствующей однородной системы (т.е. без функций ,):== 0, откуда получаем:==2 – корень кратности. В этом случае общее решение однородной системы будем искать в виде:

, и производные: (2.2)

2). Подставляем (2.2) однородную систему для заданной системы и получаем тождества:

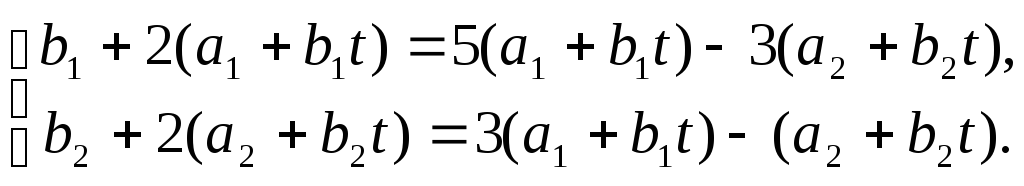(3.2)

3). Приравнивая в (3.2) коэффициенты при степенях: и, получаем систему алгебраических уравнений:откуда=, =,==. (4.2)

Замечание: решение системы (4.2)проводится по известным правилам из курса Линейная алгебра.

4). Итак, общее решение однородной системы уравнений получено:

(5.2)

5). Частное решение заданной системы уравнений, учитывая системы (1a) и (1b), запишем в виде:, (6.2)

6). Найдем частное решение неоднородной системы уравнений (1a), учитывая совпадение числас кратным характеристическим корнем:

, (7.2)

7). Подставим в (1a) выражение (7.2) и его производную: получим систему тождеств:

Из этой системы найдем неопределенные коэффициенты, приравнивая коэффициенты при одинаковых степенях :

при :при:(8.2)

при :при:

откуда получаем: ===,,. Учитывая выражение (7.2), получим частное решение для системы (1a):. (9.2)

8). Найдем частное решение неоднородной системы уравнений (1b), учитывая, что числоне совпадает с характеристическим корнем:

, (10.2)

9). Подставим в (1b) выражение (10.2) и его производную: получим систему тождеств:

откуда: a=–3, b=–2. (11.2)

10). Учитывая выражение (11.2), получим частное решение для системы (1b):

. (12.2)

11). Учитывая (9.2) и (12.2), частное решение заданной системы уравнений принимает вид:

, (13.2)

12). Запишем общее решение заданной неоднородной системы:

. (14.2)

Замечание: Выражение (14.2) получено споглощениемчислаконстантой: модификация записи общего решения.

Ответ:Общее решение:=∙.

Пример 13–03: Решить систему линейных уравнений:

Решение:

1). Найдем характеристические корни соответствующей однородной системы (т.е. без функций ,):== 0, откуда находим:=–i; =i.

2). В этом случае общее решение однородной системы будем искать в виде:

=+, (1.3)

где =∙=∙,=∙=∙, (2.3)

3). Для определения векторов ,составим систему уравнений:

(3.3)

4). Для =–iсистема (3.3) имеет решение:. Тогда можно записать:

. (4.3)

5). Для =iсистема (3.3) имеет решение:. Аналогично получаем:

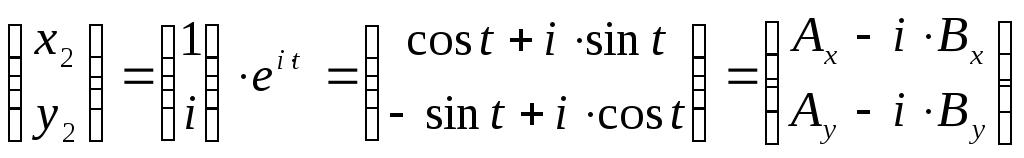. (5.3)

то есть решения и– комплексно-сопряженные.

6). В качестве частных решений системы уравнений берем отдельно мнимую и действительную части. Получаем:

=,=(6.3)

7). С учетом выражений (6.3) запишем общее решение однородной системы дифференциальных уравнений: =+. (7.3)

8). Для нахождения искомых функций _,применяют метод «вариации произвольных постоянных. Для этого считают,функциями переменной, которые находят из системы уравнений:или(8.3)

9). Так как определитель системы (3.3) не равен нулю, система имеет решение:

или после интегрирования: (9.3)

где ,– произвольные постоянные интегрирования. Подставляя (9.3) в (7.3), получим общее решение неоднородной системы уравнений:

==. (10.3)

Ответ:Общее решение:=.

☻

Вопросы для самопроверки:

1. Как по записи системы уравнений 1-го порядка определить, что она нелинейная?

2. Почему линейная система неоднородных уравнений с постоянными коэффициентами удовлетворяет требованиям теоремы «о существовании и единственности решений»?

3. Как записывают характеристический многочлен для системы линейных неоднородных уравнений с постоянными коэффициентами?

4. Как записывают общее решение системы линейных неоднородных уравнений с постоянными коэффициентами?

5. Как находят частное решение системы линейных неоднородных уравнений с постоянными коэффициентами в случае, если правая часть уравнений содержит специальные функции от независимой переменной?

6. Как находят частное решение системы линейных неоднородных уравнений с постоянными коэффициентами в случае, если правая часть уравнений содержит произвольные функции от независимой переменной?

• ◄ ≡ ► •