3.3. Среди характеристических корней системы имеются кратные.

При рассмотрении случая кратности действительных характеристических корней удобно использовать систему 3-х дифференциальных уравнений:

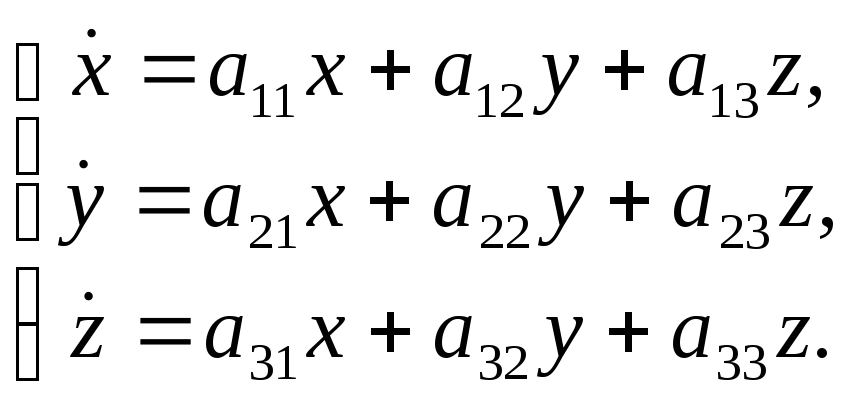(6)

3.3.1. Пусть корни ,, – действительные. В этом случае совокупность решений (9) является линейно зависимой и не может использоваться для построения ФСР и затем общего решения. Для обеспечения независимости получаемых частных решений применяют мероприятия, похожие на те, что применялись для уравнений высшего порядка. В этом случаевидприменяемыхмножителей учёта кратности корнейнесколько сложнее, но особенности достаточно быстронарабатываются!

Для лучшего восприятия используемых образов рассмотрим возможные случаи кратности корней ,,: 1)= – кратность=2; 2)== – кратность=3.

Случай–1:= – кратность=2. В этом случае заменяют два совпавших решения общей конструкцией:

= ∙и =∙→=∙(18)

Так как выражение (18) должно быть решением, то необходимо участвующие параметры подчинитьзаданной системе (6). Подставим (18) в систему (6), сократив на множитель:

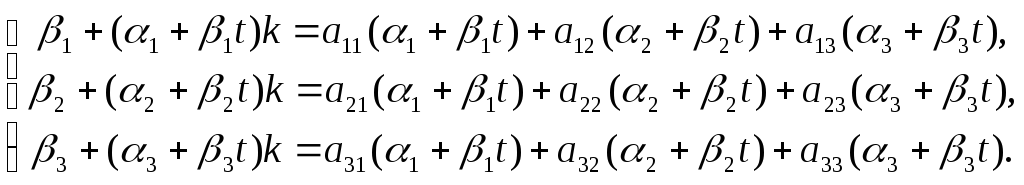(19)

В записи (19) , причём каждое уравнение является тождеством, отражающим равенство многочлена левой части равенства многочлену правой части. Приравнивая в тождествах коэффициенты при одинаковых степеняхt, получаем уравнения:

при :(20)

при :(21)

Имея системы (20) и (21) определяем порядок вычислений: из системы (20) находим все параметры ,,; затем из системы (21) находим все параметры,,. В предлагаемых Примерах системы (20), (21) достаточно просты, и все значения параметров вычисляются легко! В рассматриваемом случае произвольные постоянные появляются как значениясвободных неизвестных, сначала в системе (20). При использовании значений,,в системе (21) значениясвободных неизвестныхтакже определяются как произвольные постоянные!

Случай–2:== – кратность=3. В этом случае заменяют два совпавших решения общей конструкцией:

=∙; =∙; =∙→=∙(22)

Так как выражение (22) должно быть решением, то необходимо участвующие параметры подчинитьзаданной системе (6). Подставим (22) в систему (6), сократив на множитель:

откуда, приравнивая коэффициенты при одинаковых степенях t, получим системы:

при :(23)

при :(24)

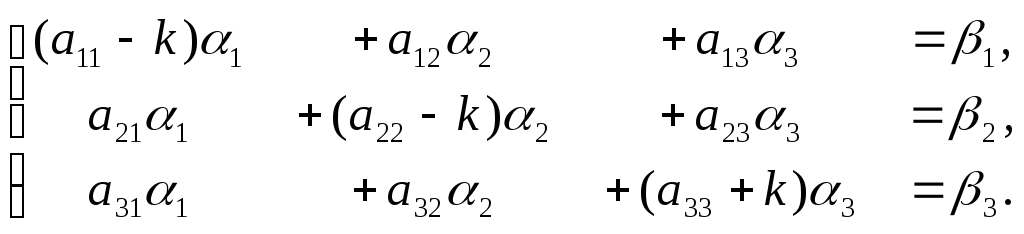при :(25)

Имея системы (23), (24) и (25) определяем порядок вычислений: из системы (23) находим все параметры ; затем из системы (24) находим все параметры,,; затем из системы (25) находим все параметры,,. В рассматриваемом случае произвольные постоянные появляются как значениясвободных неизвестных, сначала в системе (23). При использовании значенийв системе (24) значениясвободных неизвестныхтакже определяются как произвольные постоянные! При использовании значений,,в системе (25) значениясвободных неизвестныхтакже определяются как произвольные постоянные!

Дальнейшее обобщение предполагает рассмотрение системы уравнений для произвольного порядка . Пусть система записана- го и корень(действительный или комплексный!) – корень кратности. В этом случае решение системы (1) для корняищут в форме:

, (26)

где многочлены ,,…,имеют неопределенные коэффициенты (каждыйиз них имеетсвои коэффициенты, их число равно кратности корня), которые определяют из условия, что (26) является решением системы (1), т.е. из получающихся после подстановки (26) в (1) тождеств.

Для рассмотрения случая кратности комплексных характеристических корней необходимо использовать систему 4-х дифференциальных уравнений:

(6)

3.3.2. Пусть корни , – комплексные, причём: = – кратные. В этом случае совокупность решений, записываемых с использованием комплексно-сопряжённых пар характеристических корнейи, является линейно зависимой и не может использоваться для построения ФСР и затем общего решения. Для обеспечения независимости получаемых частных решений применяют мероприятия, похожие на те, что применялись для уравнений высшего порядка.

Запишем корни ,,,, подробнее:=,=,=,=. В таком случае можно воспользоваться формой записи для учета кратности корня:=– кратности 2, а затем корня:=– кратности 2. В этом случае заменяют два совпавших решения общей конструкцией:

= ∙и =∙→=∙(27)

Учтём: =и запишем для неизвестной=производную по переменной:

=++.

Аналогично можно получить выражения для остальных функций и их производных:

=→;

=→;

=→.

Подставляя ,,,,,.,в систему (6) линейных дифференциальных уравнений с постоянными коэффициентами, получаем тождества. Приравнивая коэффициенты при множителях,,,,,,,, вычисляютнеопределённые коэффициенты, для значений.

Замечание: По каждому рассмотренному случаю представлены Примеры с подробными решениями и образцами их оформления. Системы для уравнений порядкав Примерах не рассматриваются: слишком трудоёмки!

☺☺

Пример 12–05:Решить систему уравнений:

Решение:

1). Найдем характеристические корни системы: == 0, откуда получаем:==–1.В этом случае решение системы ищут в виде:=∙. (1.5)

2). Подставим (1.5) исходную систему уравнений:

(2.5)

3). Так как в системе уравнений (2.5) каждое уравнение является тождеством, то все неизвестные коэффициенты найдем, приравнивая коэффициенты при одинаковых степенях: и:

при :откуда получаем:+2=0; (3.5)

при :откуда получаем:; (4.5)

из (3.5) примем: =,=2, из (4.5):=–2; примем:=,=2+.

Замечание: решение системы (3.5), (4.5) проводится по известным правилам из курса Линейная алгебра: при назначении произвольных постоянных величин учитываются особенности конкретной решаемой системы.

4). Учитывая полученные в (3.5), (4.5) значения коэффициентов, можно записать общее решение заданной системы: =∙. (5.5)

Ответ: Общее решение:=∙.

Пример 12–06:Найти частное решение системы:для:(0)=(0)=2;(0)=–1.

Решение:

1). Найдем характеристические корни системы: == 0, откуда:==–1; =2.В этом случае решение системы для кратного корня=–1 необходимо искать в виде:

=∙. (1.6)

2). Подставим (1.6) исходную систему уравнений:

(2.6)

3). Так как в системе уравнений (2.6) каждое уравнение является тождеством, то все неизвестные коэффициенты найдем, приравнивая коэффициенты при одинаковых степенях: и:

при :откуда получаем:++=0; (3.6)

при :откуда получаем:(4.6)

Если в системе (4.6) сложить все равенства и учесть равенство (3.6), получим: ++=0. Это значит:===0. Принимая=,=вычисляем=–(+).

4). Учитывая полученные в (3.6) и (4.6) значения коэффициентов, можно представить запись решения (1.6) в виде: =∙. (5.6)

5). Для определения вектора составим систему уравнений:

(6.6)

6). Для ==2 система (5) имеет решение:=и решение:=∙∙. (7.6)

7). С учетом полученных решений (4.6) и (6.6), составим общее решение исходной системы дифференциальных уравнений (с учетом свойств матриц):

=∙+∙∙. (8.6)

8). Учитывая начальные условия и запись общего решения, получим:

=+∙, откуда=1,=1,=1.(9.6)

9). Используя результаты (8.6), запишем частное решение системы, удовлетворяющее начальным условиям: =∙+∙. (10.6)

Ответ: частное решение системы:=∙+∙.

☻