§ 4. Обобщающие примеры по теме: Элементы теории устойчивости

Набор обобщающих Примеров, представленных ниже, предназначен оказать максимальную помощь студентам, испытывающим трудности при изучении темы: Элементы теории устойчивости.

☺ ☻ ☺

Пример 14–01: Исследовать устойчивость решения уравнения: =,=1.

Решение:

1). Перепишем уравнение в виде: =.

2). Интегрируем уравнение: =t², или =. Частное решение: =0 → невозмущённое движение: =1. Возмущённое движение можно представить в виде: =. Очевидно, для любого значение неограниченно возрастает при значениях переменной . Это значит решение неустойчиво.

Ответ: решение уравнения неустойчиво.

Пример 14–02: Исследовать устойчивость решения системы: ==0.

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==0, откуда получаем:=.

2). Общее решение однородной системы будем искать в виде: =+, (1.2)

где =∙=∙,=∙=∙, (2.2)

3). Для определения векторов ,составим систему уравнений:

(3.2)

4). Для корня =система (3.2) имеет решение:=. Для=: =.

5). С учетом полученных векторов ,запишем общее решение однородной системы дифференциальных уравнений:=∙∙+∙∙. (4.2)

6). С учетом начальных данных получим:

=∙+∙, откуда=0,=0. (5.2)

Это значит: невозмущенное движение – тривиальное и исследование устойчивости осуществляется исследованием величин характеристических корней системы!

7). Так как один из действительных корней положителен, то система неустойчива: седло.

Ответ: система неустойчива: седло.

Пример 14–03: Исследовать устойчивость решения системы: ===0.

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==, откуда получаем характеристические корни:=,=+,=.Для каждого,определится набор коэффициентов:,,, что определит полный набор решений заданной системы:

==∙,=∙=∙,=∙=∙, (1.3)

2). Для определения векторов ,,составим систему уравнений:

(2.3)

3). Для корня =решение системы (2.3):=→=∙=∙.

4). Для корня =+система (2.3) имеет решение:=, тогда можно записать частное решение для характеристического корня:

=∙=∙=.

5). Для корня =получим частное решение:=. Это значит, что в качестве решений системы можно записать:=,=. Вычисление указанных величин не вызывает затруднений. Окончательно запишем:

=∙,=∙.

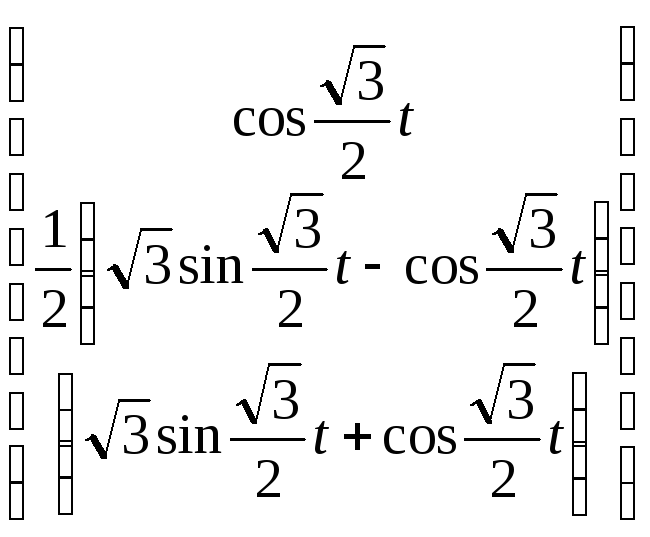6). С учетом полученных векторов ,,составим общее решение исходной системы дифференциальных уравнений (с учетом свойств матриц):

=++=

7). С учетом начальных данных получим:

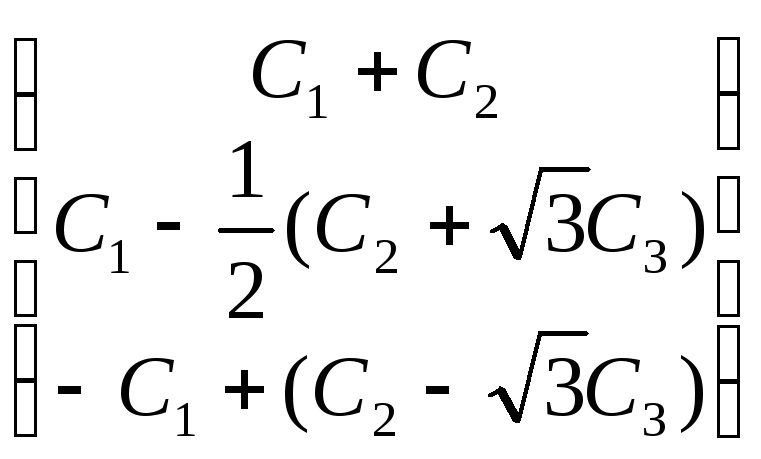=, откуда=0,=0,=0. (3.3)

Это значит: невозмущенное движение – тривиальное и исследование устойчивости осуществляется исследованием величин характеристических корней системы!

7). Так как один из действительных корней положителен, то система неустойчива: седло.

8). Рассмотрим поведение системы в зависимости от значений параметра :

▪ при α< – корни: < 0, < 0 → асимптотическая устойчивость;

▪ при α = – корни: < 0, =0 → устойчивость;

▪ при α > – корни: > 0, > 0 → неустойчивость.

Ответ: устойчивость системы зависит от значений параметра .

Пример 14–04: Исследовать устойчивость решения системы в точке покоя:

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==0, откуда получаем:=–±.

2). Так как один из действительных корней положителен, то система неустойчива: седло.

Ответ: система неустойчива: седло.

Пример 14–05: Исследовать устойчивость решения системы в точке покоя:

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==0, откуда получаем:=–1.

2). Так как корни =–1<0, то система асимптотически устойчива: устойчивый узел.

Ответ: система неустойчива: устойчивый узел.

Пример 14–06: Исследовать устойчивость решения системы в точке покоя:

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==0, откуда получаем:=–3.

2). Так как корни =–3<0, то система асимптотически устойчива: устойчивый узел.

Ответ: система неустойчива: устойчивый узел.

Пример 14–07: Исследовать устойчивость системы в точке покоя:

Решение:

1). Найдем характеристические корни заданной однородной системы дифференциальных уравнений: ==0, откуда получаем:=.

2). Рассмотрим поведение системы в зависимости от значений параметра :

▪ при |α|< корни действительные: < 0, > 0 → неустойчивость;

▪ при |α|= корни: ==0 → неустойчивость;

▪ при <|α|<2 корни действительные: <0, <0 → асимптотическая устойчивость;

▪ при |α|=2 корни: ==2 → асимптотическая устойчивость;

▪ при |α|>2 корни комплексные: =→ асимптотическая устойчивость.

Ответ: устойчивость системы зависит от значений параметра .

Пример 14–08: Исследовать на устойчивость «по первому приближению» нулевого решения системы дифференциальных уравнений:

Решение:

1). Воспользуемся разложениями (из задачника): ,. Так как условие теоремы:выполняется, то оценку устойчивости решений можно уценивать на основании линеаризованной системы уравнений:

2). Найдем характеристические корни полученной однородной системы дифференциальных уравнений: ==0, откуда получаем:=.

3). Так как >0, то система неустойчива: неустойчивый узел.

Ответ: система устойчива: неустойчивый узел.

Пример 14–09: Исследовать на устойчивость «по первому приближению» нулевого решения системы дифференциальных уравнений:

Решение:

1). Воспользуемся разложениями (из задачника): . Так как:выполняется, то (согласно Теореме) устойчивости решений можно уценивать на основании линеаризованной системы уравнений:

2). Найдем характеристические корни полученной однородной системы дифференциальных уравнений: ==0, откуда получаем:==.

3). Так как <0, , то система устойчива: асимптотически устойчива.

Ответ: система устойчива: устойчивый фокус.

☻

Вопросы для самопроверки:

1. Каково назначение раздела теории ДУ: теория устойчивости?

2. Что такое: невозмущённое движение и возмущённое движение?

3. Что такое точка покоя?

4. Что значит: устойчивость тривиального решения системы?

5. Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы действительные, разные?

6. Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы комплексные?

7. Какие случаи устойчивости точки покоя реализуются, если характеристические корни системы действительные, кратные?

8. Как случаи устойчивости точки покоя изображаются на комплексной плоскости?

• ◄ ≡ ► •