
- •Глава 5. Кривые и поверхности второго порядка §1 . Эллипс, гипербола и парабола Эллипс
- •Уравнение эллипса в канонической системы координат
- •Гипербола
- •Уравнение гиперболы в канонической системе координат
- •П арабола
- •§ 2. Приведение к каноническому виду уравнения кривой второго порядка
- •§ 3. Полярная, сферическая и цилиндрическая системы координат
- •§ 4. Поверхности
- •Коническая поверхность
- •Цилиндрическая поверхность
- •Поверхность вращения
- •§ 5. Поверхности второго порядка
- •Задачи для самостоятельного решения
§ 2. Приведение к каноническому виду уравнения кривой второго порядка
Общее уравнение кривой второго порядка имеет вид
![]()
причем
предполагается, что среди чисел
![]() есть хотя бы одно ненулевое.
есть хотя бы одно ненулевое.
Существует система координат (называемая канонической), в которой уравнение кривой второго порядка имеет вид, приведенный в таблице (канонический вид).
|
|
эллипс |
|
|
гипербола |
|
|
парабола |
|
|
мнимый эллипс (эта “кривая” не имеет действительных точек) |
|
|
на действительной плоскости “кривая” имеет лишь одну точку |
|
|
две пересекающиеся прямые |
|
|
две параллельные прямые |
|
|
две совпадающие прямые |
|
|
две мнимые параллельные прямые (“кривая” не имеет ни одной действительной точки) |
Задача 1. Изобразить кривую, найти ее характеристики:
![]()
Р

![]() и по
и по![]()
![]()
![]()
![]() Следовательно, данная кривая является
эллипсом. Его центр:
Следовательно, данная кривая является
эллипсом. Его центр:![]() Полуоси:
Полуоси:![]()
![]() Для нахождения координат фокусов находим
параметр
Для нахождения координат фокусов находим
параметр![]() (половину расстояния между фокусами):
(половину расстояния между фокусами):![]() Отсюда получаем фокусы:
Отсюда получаем фокусы:![]()
![]() Эксцентриситет:
Эксцентриситет:![]()
Задача 2.
Составить
уравнение гиперболы с асимптотами
![]() касающейся оси
касающейся оси![]()
Р

![]() имеют вид
имеют вид![]() Следовательно, центр гиперболы имеет
координаты
Следовательно, центр гиперболы имеет
координаты
![]() и
и
![]() Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Нарисуем гиперболу, учитывая, что она
касается оси абсцисс.
Из
рисунка видно, что
![]() Так как
Так как![]() то
то![]() Так как действительная ось гиперболы
параллельна оси
Так как действительная ось гиперболы
параллельна оси![]() то в правой части уравнения будет
то в правой части уравнения будет![]() вместо
вместо![]() Отсюда получаем уравнение:
Отсюда получаем уравнение:
![]()
Задача 3.
Найти площадь
области, ограниченной кривой
![]()
Решение.
В случае, когда коэффициенты при
![]() и
и![]() равны друг другу, то поворотом системы
координат на угол в
равны друг другу, то поворотом системы
координат на угол в![]() можно избавиться от произведения
можно избавиться от произведения![]() в уравнении кривой. Напишем формулы
поворота на угол
в уравнении кривой. Напишем формулы
поворота на угол![]()
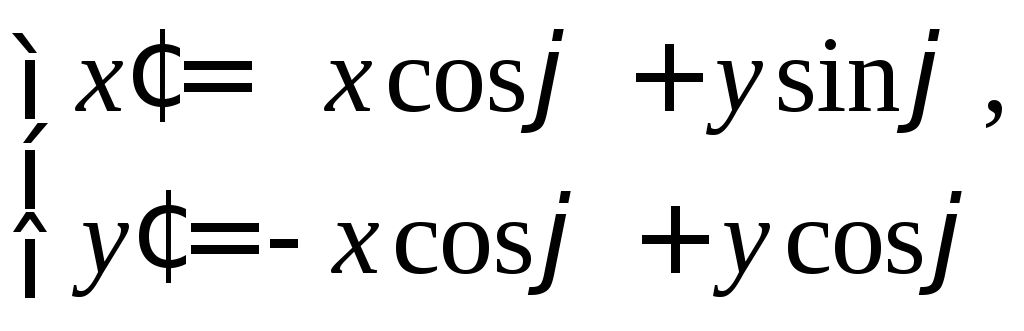

(здесь
![]() – координаты точки в исходной системе
координат, а
– координаты точки в исходной системе
координат, а![]() – координаты той же точки в системе
координат, повернутой на угол
– координаты той же точки в системе
координат, повернутой на угол![]() .
При
.
При![]() получаем прямые и обратные формулы:
получаем прямые и обратные формулы:



Подставим обратные формулы в уравнение кривой:

![]()
![]()
 Следовательно,
Следовательно,
![]()
![]() .
Отсюда
.
Отсюда![]()
)
Рис.
5.30![]() и
и![]() (его полуоси). Далее строим отрезок
(его полуоси). Далее строим отрезок![]() (рис. 5.34) и фокусы
(рис. 5.34) и фокусы![]() эллипса.
эллипса.
Задача 4. Установить, что уравнение
![]()
определяет эллипс, найти его центр и полуоси.
Решение. Преобразуем это уравнение:
![]() ,
или
,
или
![]() ,
или
,
или
![]()
 .
.
Положим
![]() и уравнение примет вид
и уравнение примет вид![]() Это уравнение эллипса с полуосями
Это уравнение эллипса с полуосями![]() и
и![]() .
.
Задача
5.
Установить, что уравнение
![]() определяет гиперболу, найти ее центр и
полуоси.
определяет гиперболу, найти ее центр и
полуоси.
Подберём
угол
![]() ,
после поворота на который уравнение
кривой не будет содержать произведения
переменных
,
после поворота на который уравнение
кривой не будет содержать произведения
переменных![]() и
и![]() .
Подставим формулы поворота в заданное
уравнение
.
Подставим формулы поворота в заданное
уравнение![]() ,
которое лучше переписать в виде
,
которое лучше переписать в виде![]() :
:
![]() ,
,
![]() ,
,
 .
.
Найдём
такой угол
![]() ,
чтобы в последнем уравнении не содержалось
слагаемое
,
чтобы в последнем уравнении не содержалось
слагаемое![]() .
Достаточно положить,
.
Достаточно положить,![]() ,
то есть
,
то есть![]() ,
,![]() .
.
Тогда преобразование примет вид


-
поворот против часовой стрелки вокруг
точки
![]() ,
а уравнение кривой (5.28) в новой системе
координат:
,
а уравнение кривой (5.28) в новой системе
координат:
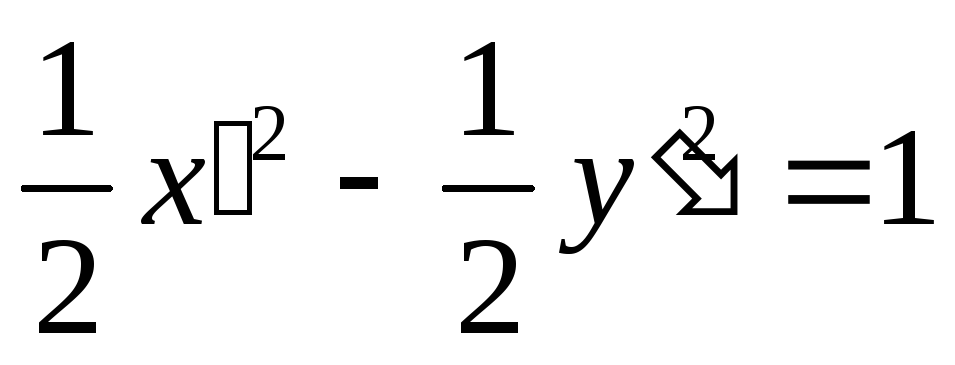
-
это уравнение гиперболы с полуосями
![]() и
центром в точке
и
центром в точке
![]() (рис. 5.16).
(рис. 5.16).
