Физика, элементарные определения и формулы / 3_Законы сохранения

3. Законы сохранения в механике

Изменение импульса тела равно импульсу силы:

Система тел, для которой внешние силы отсутствуют или равнодействующая всех внешних сил равна нулю, называется замкнутой. Если система тел замкнута,

Если внешние силы перпендикулярны некоторой оси x, то проекция импульса системы на это направление сохраняется:

Если время взаимодействия мало (взрыв, удар), а внешняя сила имеет

где α – угол между силой и перемещением, Fs – проекция силы на перемещение. Работа силы, линейно зависящей от перемещения:

Здесь F1s и F2s – проекции силы на перемещение в начальной и конечной точках.

Средняя мощность за время t:

ср t

Мгновенная мощность определяется формулой

где α – угол между силой и скоростью точки приложения силы, Fv – проекция силы на скорость.

Кинетическая энергия материальной точки:

Теорема об изменении кинетической энергии:

Eк = Eк2 −Eк1 = A . (12)

Здесь Eк – изменение кинетической энергии тела, A – суммарная работа всех действующих на тело сил.

Консервативные силы – силы, работа которых не зависит от формы траектории. Для них можно ввести понятие потенциальной энергии. Работа консервативных сил равна убыли потенциальной энергии:

Здесь высота h отсчитывается от произвольно выбранного нулевого уровня. Потенциальная энергия упруго деформированной пружины:

В формуле (15) за ноль принята потенциальная энергия недеформированной пружины.

Механическая энергия системы тел сохраняется, если эта система является замкнутой и , кроме того, в ней действуют только консервативные силы (закон сохранения механической энергии):

Изменение механической энергии системы тел равно суммарной работе внешних сил и внутренних сил трения (закон изменения механической энергии):

Количество энергии, перешедшей во внутреннюю за счет трения (количество выделившейся теплоты), равно абсолютной величине работы сил трения:

2. Санки после толчка движутся по горизонтальной дороге. Как изменится модуль импульса санок, если на них в течение 5 с действует сила трения о снег, равная 20 Н?

А) ответить невозможно, так как неизвестна масса санок; Б) увеличится на 4 кг·м/с; В) увеличится на 100 кг·м/с; Г) уменьшится на 100 кг·м/с.

3. На сани, стоящие на гладком льду, с некоторой высоты прыгает человек массой 50 кг. Проекция скорости человека на горизонтальное направление в момент соприкосновения с санями 4 м/с. Скорость саней с человеком после

4. Человек тянет брусок массой 1 кг по горизонтальной поверхности с постоянной скоростью, прикладывая к нему силу в горизонтальном направлении. Коэффициент трения между бруском и поверхностью равен 0,1. Скорость движения бруска 10 м/с. Какую мощность развивает человек, перемещая груз?

А) 0,1 Вт; Б) 100 Вт; В) 0 Вт; Г) 10 Вт.

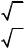
5. Для того, чтобы уменьшить кинетическую энергию тела в 2 раза, надо его

6. Недеформированную пружину жесткостью 30 Н/м растянули на 4 см.

7. Шарик массой m движется со скоростью v. После упругого соударения со стенкой он стал двигаться в противоположном направлении, но с такой же по модулю скоростью. Чему равна работа силы упругости, которая подействовала на

8. Шарик массой 100 г, движущийся со скоростью 1 м/с, абсолютно упруго ударяется о горизонтальную плоскость. Направление скорости шарика составляет с плоскостью угол 30˚. Определите модуль изменения импульса шарика в результата удара.

А) 0,3 кг·м/с; Б) 0,2 кг·м/с; В) 0,17 кг·м/с; Г) 0,1 кг·м/с.

9. Шарик брошен вертикально вверх. В момент броска он имел кинетическую энергию 30 Дж. На сколько изменится потенциальная энергия шарика в поле тяготения Земли, когда он окажется в верхней точке траектории? Сопротивлением

наклона плоскости к горизонту равен 30˚. Чтобы тащить вверх по этой плоскости ящик массой 120 кг, к нему надо приложить силу, направленную параллельно плоскости и равную

А) 480 Н; Б) 600 Н; В) 750 Н; Г) 1040 Н.

Примеры решения задач

Пример 1. При выстреле из пушки массой M = 800 кг вылетает снаряд под углом α = 45° к горизонту. При этом пушка за счет отдачи откатывается в горизонтальном направлении с начальной скоростью V = 0,5 м/с. Найдите изменение импульса p системы «пушка-снаряд» в результате такого выстрела. Трением пренебречь.

Р е ш е н и е. Заметим, что импульс системы «пушка-снаряд» изменяется при выстреле в результате действия на систему внешней силы – силы реакции опоры. Однако сохраняется горизонтальная составляющая импульса системы, поскольку сила реакции опоры не имеет проекции на это направление. Поэтому должны выполняться следующие равенства:

0 = mu cos α −MV , p =mu sinα.

Здесь u – скорость вылетающего из пушки снаряда, p – искомое изменение импульса системы. В результате имеем p = MVtgα= 400 кгּм/с.

Пример 2. Тело брошено вертикально вверх со скоростью V0 = 49 м/с. На какой высоте h его кинетическая энергия будет равна потенциальной? Ускорение свободного падения g = 9,8 м/с2. Потенциальную энергию в точке старта примите равной нулю.

Р е ш е н и е. Пренебрегая сопротивлением воздуха, запишем закон сохранения

Здесь m – масса тела, h – искомая высота, V – скорость тела на высоте h. По условию задачи на этой высоте

mV2 2 = mgh.

Тогда из закона сохранения механической энергии имеем

Пример 3. С вершины гладкой наклонной плоскости высотой H = 20 см соскальзывает брусок. Определите скорость V бруска в конце плоскости. Ускорение свободного падения g = 10 м/с2. Начальная скорость равна нулю.

Р е ш е н и е. Примем основание горки за нулевой уровень потенциальной энергии. Поскольку трение отсутствует, механическая энергия бруска сохраняется. Приравнивая значения механической энергии на вершине горки и у ее основания, получим

0 +mgH = mV2 2 + 0 .

Отсюда находим скорость бруска у основания плоскости:

V = 2gH = 20 м/с.

Пример 4. Шайба с нулевой начальной скоростью скользит с высоты H по гладкой наклонной плоскости, образующей угол α с горизонтом. В конце наклонной плоскости она встречает гладкую горизонтальную плоскость. Найдите максимальную высоту h подъема шайбы после абсолютно упругого удара о

составляющую VГ . Приравнивая значения механической энергии в двух точках – на высоте H и в вершине параболы на высоте h – получим уравнение

0 +mgH = mV2Г2 +mgh .

Здесь m – масса пули, M – масса шара, V и u – скорости пули и шара сразу после вылета пули из шара (рис. 2).

а) После вылета пули из шара он приобретает кинетическую энергию Mu2 2 ,

которая полностью переходит в потенциальную энергию при подъеме на высоту h = L − L cos α = L(1 −cos α):

Mu2 2 = Mgh .

Отсюда u = 2gl(1 −cos α) . По условию α = 60° и, следовательно, cos α = 12 .

Тогда u = gl .

б) Подставляя найденное значение u в закон сохранения импульса и учитывая, что по условию задачи M =10m , получим

mV0 = mV +10m gl .

Окончательно для скорости V пули после вылета из шара имеем

V =V0 −10 gl .

Задачи для самостоятельного решения

Задача 1. Тело массой m = 1 кг бросили под углом к горизонту. В высшей точке траектории на высоте h = 20 м его кинетическая энергия Eк = 200 Дж. Под каким углом α к горизонту бросили тело? Ускорение свободного падения g = 10 м/с2. Сопротивлением воздуха пренебречь.

Задача 2. Тело массой m = 1 кг брошено под углом к горизонту. За время полета его импульс изменился на p = 10 кг м/c. Определите максимальную высоту Н подъема тела. Сопротивлением воздуха пренебречь. Ускорение свободного падения g = 10 м/с2.

pG 2

Ответ: H = 8m2g =1,25 м .

Задача 3. Концы недеформированной пружины закреплены. Какую работу следует совершить, чтобы, взявшись за средний виток пружины, медленно переместить его на x = 2 см вдоль оси пружины? Жесткость пружины (всей, а не ее половины) равна k = 100 Н/м.

О т в е т: A = 2kx2 =0,08 Дж .

Задача 4. При формировании железнодорожного состава два одинаковых, сцепленных между собой вагона, движущиеся со скоростью V0 = 0,4 мс,

сталкиваются с неподвижным вагоном той же массы. Определите скорость V движения вагонов после сцепки.

О т в е т: V = 32V0 ≈ 0,27 м/с.

Задача 5. Маленькая шайба, движущаяся по гладкой горизонтальной поверхности, въезжает на шероховатый участок шириной L =1 м перпендикулярно границе участка. При какой наименьшей скорости V0 шайба преодолеет участок, если коэффициент трения на нём линейно возрастает от μ1 = 0,3 до μ2 = 0,6?

Ответ: V0 = (μ1 +μ2 )Lg =3 мс.

Задача 6. Пружину деформировали, совершив работу А1. Какую работу А2 надо совершить, чтобы увеличить деформацию в n = 2 раза?

Ответ: A2 =3A1 =(n2 −1) A1 .

Задача 7. Свободное тело разогнали из состояния покоя, совершив работу А = 1 Дж, а затем остановили, прикладывая тормозящую силу F = 2 Н в течение времени t = 1 с. Определите массу m тела.

О т в е т: m = F 2t2 = 2 кг.

2A

Задача8. Шар массой m = 3 кг, имеющий скорость v = 2 м/с, испытал абсолютно неупругий центральный удар с покоящимся шаром массой 2m. Определите количество тепла Q, выделившегося при ударе.

Ответ: Q = m3v2 = 4 Дж.

Задача 9. При колебаниях математического маятника наибольшая высота подъема его груза h = 1,8 см. Найдите импульс p груза при прохождении им положения равновесия. Масса груза m = 100 г.

Ответ: p = m 2gh =0,06 кг м/с.

Задача 10. Тело движется поступательно вдоль оси