Электротехника Начало семестра / ДЗ 1

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

Кафедра: ЭЛЕКТРОТЕХНИКА (ЭТ) Дисциплина: Электротехника

Пояснительная записка к домашней работе (ДЗ №2 вариант №16) на тему:

Линейные электрические цепи постоянного тока. МКТ, МУП, МЭГ

Руководитель: Ю. И. Волков Выполнил: Дата: Оценка:

Москва 2013

Задача 1

Дано:

,

,

,

,

,

,

,

,

.

Определить:

1. токи всех ветвей, используя МКТ, МУП;

2. ток в выделенной ветви, используя МЭГi, МЭГu;

3. проверить баланс мощностей;

4. привести схемы в EWB или Ms для измерения токов ветвей, напряжений на элементах, мощностей источников и приемников.

Метод контурных токов

Количество уравнений:

Рассчитаем контурные токи:

Найдём токи ветвей:

Метод узловых потенциалов

Количество уравнений:

По закону Ома:

Составим систему уравнений по первому закону Кирхгофа для узлов и :

Найдём токи ветвей:

По первому закону Кирхгофа:

Проверка

По первому закону Кирхгофа:

Потенциальная диаграмма

Контур

Метод эквивалентного генератора напряжения

Найдём ток методом эквивалентного генератора напряжения:

1. Исключим из схемы ветвь с неизвестным током.

Пусть потенциал узла .

Чтобы найти потенциалы на зажимах и необходимо найти токи и . Для этого воспользуемся методом контурных токов.

Количество уравнений по МКТ:

Получим уравнение:

Найдём токи:

По закону Ома найдём потенциалы на узлах и :

Потенциалы и будут равны и соответственно.

Найдём напряжение холостого хода :

2. Исключим из схемы источники тока и ЭДС, заменив источники тока разрывом, а источники ЭДС – короткозамкнутым отрезком.

Рассчитаем эквивалентное сопротивление :

3. Составим одноконтурную цепь, и подключим к ней ветвь, удалённую из исходной схемы:

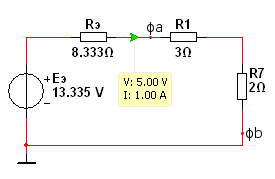
Найдём ток :

Метод эквивалентного генератора тока

1. Заменим ветвь с искомым током короткозамкнутым отрезком:

2. Положим, значения всех источников кроме

3. Положим значения всех источников кроме

По 1-му закону Кирхгофа:

По закону Ома:

Подставим токи в уравнение по Кирхгофу:

(

Найдём ток :

4. Положим значения всех источников кроме :

По 1-му закону Кирхгофа:

5. Составим одноконтурную цепь и подключим к ней ветвь удалённую из исходной схемы:

По формуле делителя тока:

(по закону Ома)

, где

(по закону Ома)

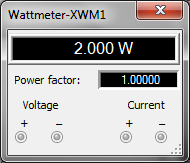
Баланс мощностей

Граф цепи:

, где - напряжение на источнике тока.

, где – потенциал в точке между и. Найдём из закона Ома для тока на :

Подставимвыражение для в выражение для :

Подставим в выражение для :

Задача 2

Дано:

,

,

,

,

,

,

,

,

.

Определить:

1. токи всех ветвей, используя МКТ, МУП;

2. ток в выделенной ветви, используя МЭГi, МЭГu;

3. проверить баланс мощностей;

4. привести схемы в EWB или Ms для измерения токов ветвей, напряжений на элементах, мощностей источников и приемников.

Метод контурных токов

Количество уравнений:

Рассчитаем контурные токи:

Найдём токи ветвей:

Метод узловых потенциалов

Количество уравнений:

По закону Ома:

Составим систему уравнений по первому закону Кирхгофа для узлов и :

Найдём токи ветвей:

По первому закону Кирхгофа:

Проверка

По первому закону Кирхгофа:

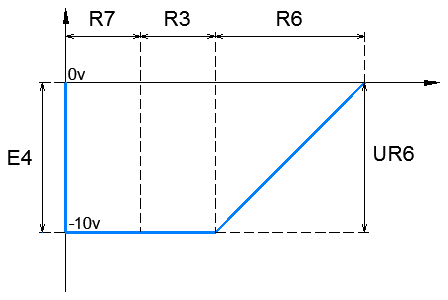
Потенциальная диаграмма

Контур

Метод эквивалентного генератора напряжения

Найдём ток методом эквивалентного генератора напряжения:

1. Исключим из схемы ветвь с неизвестным током.

Пусть потенциал узла , тогда потенциал .

Чтобы найти потенциал на зажиме необходимо найти ток . Для этого воспользуемся методом контурных токов.

Количество уравнений по МКТ:

Получим уравнение:

Найдём ток:

По закону Ома найдём потенциал на узле :

Потенциал будет равен .

Найдём напряжение холостого хода :

2. Исключим из схемы источники тока и ЭДС, заменив источники тока разрывом, а источники ЭДС – короткозамкнутым отрезком.

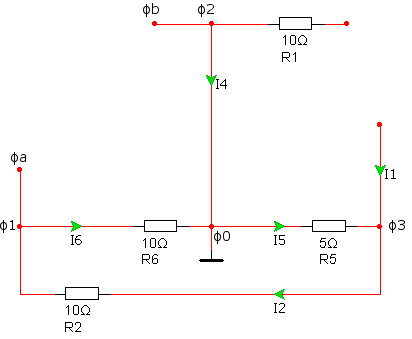
Рассчитаем эквивалентное сопротивление :

3. Составим одноконтурную цепь, и подключим к ней ветвь, удалённую из исходной схемы:

Найдём ток :

Метод эквивалентного генератора тока

1. Заменим ветвь с искомым током короткозамкнутым отрезком:

2. Положим, значения всех источников кроме