3.9. Матрицы, связанные с графами

В этом параграфе наряду с неориентированными графами будем рассматривать ориентированные графы, которые мы будем называть орграфами. Граф всегда обозначает граф без петель навершинах ирёбрах.

Определение 1. Пусть – перенумеруем его вершины:. Матрицуразмера, в которой

будем называть матрицей смежности графа .

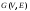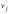Предложение 1. Пусть – граф, в котором вершины перенумерованы и– его матрица смежности. Тогда элементматрицыравен числу маршрутов между вершинамиидлины.

Определение 2. Пусть – граф, на каждом ребре которого задано направление. Такой граф будем называть орграфом. Рёбра орграфа будем называть дугами. Если направление на дугезадано от вершинык вершине, то будем говорить, что дугаисходит из вершиныи заходит в вершину.

Определение 3. Пусть – орграф, в котором перенумерованы вершины и дуги. Матрицей инцидентности графа называется матрицаразмера, элементы которой определяются следующим образом:

Всякий столбец матрицы орграфа содержит два ненулевых элемента –1 и 1. Поэтому любую строчку этой матрицы можно определить по остальнымстрокам.

Определение 4. Матрицу , полученную из матрицывычёркиванием одной произвольной строки, будем называть усечённой матрицей инцидентности.

Очевидно, ранги матриц исовпадают и не превосходят.

Теорема 1. Определитель любой усечённой матрицы инцидентности дерева равен .

Доказательство. Индукция по числу вершин . Дляутверждение верно.

Пусть теорема выполняется для числа вершин , и– дерево с-й вершиной, а– его усечённая матрица инцидентности. Деревоимеет, по крайней мере, две висячие вершины, и по крайней мере, одна строка матрицысоответствует этой вершине. В этой строке (обозначим её) только один ненулевой элемент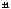. Пусть вершинаинцидентна-му ребру. Матрицу, полученную извычёркиванием-й строки и-го столбца, обозначим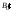. Тогда. Поскольку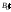– усечённая матрица для дерева, полученного изудалением-й вершины и-го ребра, топо предположению индукции.

Теорема доказана.

Следствие. Ранг матрицы инцидентности связного графа навершинах равен.

Определение 5. Пусть имеется связный граф и его остов. Перенумеруем сначала хорды, а потом ветви графа. Каждому фундаментальному разрезу придадим ориентацию, совпадающую с ориентацией соответствующей ветви. Матрицу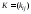размера, строки которой соответствуют фундаментальным разрезам, а столбцы – дугам орграфа, будем называть матрицей фундаментальных разрезов, если:

Определение 6. Пусть имеется связный граф и его остов. Перенумеруем сначала хорды, а потом ветви графа. Каждому фундаментальному циклу придадим ориентацию, совпадающую с ориентацией соответствующей хорды. Матрицуразмера, строки которой соответствуют фундаментальным циклам, а столбцы – дугам орграфа, будем называть матрицей фундаментальных циклов, если

Следующие три теоремы приведём без доказательства.

Теорема 2. Пусть – связный граф,– его остов,– матрицы инцидентности, фундаментальных разрезов и фундаментальных циклов соответственно. Тогда

.

Определение 7. Матрица размераназываетсяунимодулярной, если определитель любой её квадратной подматрицы равен 1, –1 или 0.

Теорема 3. Матрицы инцидентности, фундаментальных циклов и фундаментальных разрезов связного графа унимодулярны.

Теорема 4. Пусть – связный граф,– усечённая матрица инцидентности какой-либо из ориентаций графа. Тогда число остовов графаравно.