3.4. Помеченные графы. Код Прюфера

Определение 1. Граф будем называть помеченным, если каждой вершине присвоена своя метка. Обычно полагают. Два помеченных графаисчитаются одинаковыми в точности тогда и только тогда, когдаи.

Пример 1. Следующие помеченные графы являются разными.

А помеченные графы

одинаковы.

Предложение 1. Число помеченных -графов равно.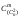

Доказательство. Существует неупорядоченных пар вершин, которые можно соединить ребром. Если нужно выбратьрёбер, тоэто можно сделатьспособами.

Предложение доказано.

Например, число помеченных графов с 4-мя вершинами и 5-ю рёбрами равно . Все они изображены в начале этого параграфа.

Предложение 2. Число помеченных графов на вершинах равно.

Доказательство. Множество рёбер каждого помеченного графа на вершинах есть некоторое подмножество в множестве всевозможных рёбер, число которых, как было сказано выше, равно. Число таких подмножеств есть.

Предложение доказано.

Пример 2. Число помеченных графов на 3-х вершинах равно . Вот они

Поясним, что помеченное дерево – это помеченный граф, являющийся деревом.

Теорема (Кэли). Число помеченных деревьев на вершинах равно.

Доказательство этой теоремы может быть основано на следующем алгоритме, сопоставляющем каждому дереву некоторую последовательность номеров его вершин, которая называется кодом Прюфера этого дерева. Опишем этот алгоритм.

Пусть имеется помеченное дерево навершинах. Как минимум две его вершины являются висячими. Пусть– висячая вершина с наименьшим номером, а– соответствующее висячее ребро. Удалив из деревареброи вершину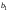, получим новое дерево. Дляопять найдём висячую вершинус наименьшим номером. Соответствующее висячее ребро обозначими т.д. Продолжим эту процедуру до тех пор, пока у нас не останется единственное ребро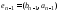. Набори будет кодом Прюфера дерева.

Каждый код Прюфера, т.е. любой набор из чисел, каждое из которых может принимать значения от 1 до, однозначно соответствует своему дереву. В этом можно убедиться с помощью следующей обратной процедуры.

Действительно, пусть имеется код . Запишем последовательность натуральных чисел от 1 до:. Среди этих чисел находим наименьшее число, не содержащееся в коде. Пусть это будет. рисуем ребро. Числоудаляем из кода, а числоудаляем из набора. Далее, в наборенаходим наименьшее число, не содержащееся в оставшейся части кода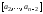. Пусть это будет. Изображаем ребро. Далее, рассматриваем часть кода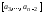и набор. Продолжим эту процедуру до тех пор, пока в наборене останутся лишь две вершины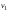и. Соединим их ребром, Мы получили дерево навершинах.

Можно показать, что указанное соответствие между помеченными деревьями на вершинах и всевозможными кодами Прюфера, состоящими изчисел, является взаимно однозначным.

Пример 3. Дерево

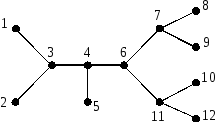
имеет код .

Задачи.

Перенумеруйте вершины дерева и найдите его код Прюфера.

1.
2.

По заданному коду Прюфера восстановите помеченное дерево.

3. .

4. .

3.5. Алгоритм Краскала

На языке помеченных графов формулируются многие виды прикладных задач. В данном и следующем параграфах мы рассмотрим две из них.

Допустим, нужно построить сеть железных дорог, которые соединили бы данных городов так, чтобы из каждого города можно было бы приехать в любой другой город. Пусть для каждой пары городов известна стоимость строительства дороги между ними. Как построить дерево, соединяющее этигородов, чтобы общая стоимость строительства была минимальной?

Алгоритм решения данной задачи известен под названием алгоритма Краскала.

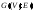Определение 1. Граф называется взвешенным, если каждому его ребруприсвоено некоторое действительное число, называемое его весом. Другими словами, задана функция. Если задан подграфграфа, то его весом называется.

Определение 2. Пусть имеется связный граф . Связный подграфграфа, содержащий все вершины графаи являющийся деревом, называется остовом графа.

Связный граф может иметь много остовов.

Таким образом, задача о соединении городов сводится к нахождению остова наименьшего веса.

Теорема. Пусть – связный граф на вершинах. Тогда следующая процедура приводит к решению задачи о соединении городов:

1. выберем ребро , обладающее внаименьшим весом;

2. определим по индукции последовательность рёбер , выбирая на каждом шаге ребро, отличное от предыдущих, не образующее циклов с множеством предыдущих рёбер, и обладающее среди таких ребер наименьшим весом.

Полученный подграф графа, ребрами которого являютсяи есть требуемое дерево.

Доказательство. Поскольку без циклов и, то– дерево, что следует из теоремы 1 параграфа 3.2. Покажем, что сумма весом рёбер дереваминимальна.

Допустим противное, т.е. что существует дерево , для которого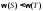. Пусть– рёбра дерева, принадлежащие также и, а– первое ребро из, не принадлежащее. Подграф графа, полученный присоединением ребракдаёт единственный цикл. Так как, то циклсодержит ребро, не принадлежащее. Обозначим его. Подграф, полученный иззаменойна, по-прежнему является деревом (как связный граф, в котором), причём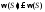ииимеют общие рёбра. Продолжая этот процесс, преобразуемв. Но тогда. Противоречие.

Теорема доказана.

Пример. Пусть имеется следующая матрица стоимостей строительства дорог

	1	2	3	4	5	6
1		13	14	12	15	16
2			9	7	5	6
3				8	11	10
4					1	2
5						2
6						

Требуется найти остов наименьшего веса.

Сначала выбираем ребро наименьшего веса 1. Далее, берём ребронаименьшего веса 2. Следующим ребром наименьшего веса является ребро. Но оно образует цикл с предыдущими двумя рёбрами. Поэтому мы его пропускаем и берём следующее ребро наименьшего веса. Далее, рёбраиобразуют циклы с предыдущими рёбрами. Мы их пропускаем и берём ребро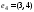. Рёбра,имы взять не можем, поэтому следующим ребром, удовлетворяющим условиям алгоритма, будет ребро. 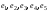Рёбраобразуют остов наименьшего веса 28. Соответствующий план дорог изображён ниже.