3. Графы

3.1. Введение в графы. Задача о кёнигсбергских мостах. Проблема четырёх красок

Начало теории графов все единодушно относят к 1736 году, когда Леонард Эйлер (1707 – 1783) не только решил популярную в то время задачу о кёнигсбергских мостах, но и нашёл критерий существования в графе специального маршрута (эйлерова цикла, как теперь его называют). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Густав Кирхгоф (1824 – 1895) разработал теорию деревьев для исследования электрических цепей, а математик Артур Кэли (1821 – 1895) в связи с описанием строения углеводородов решил перечисленные задачи для трёх типов деревьев. К этому же периоду относится появление знаменитой проблемы четырёх красок.

Остановимся поподробнее на задаче о кёнигсбергских мостах. Суть её в следующем. В г.Кёнигсберге посередине реки были два острова. Эти острова соединялись между собой и с обоими берегами реки системой мостов. Если каждый отделённый участок суши обозначить точкой, а каждый мост изобразить «ребром», то получится следующая схема.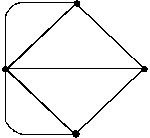

Точку (вершину) назовём чётной, если из неё выходит чётное число рёбер, и нечётной в противном случае. Решение Эйлера состояло в следующем. «Граф» можно обойти, если число нечётных вершин равно 0 или 2. В данном случае все четыре вершины являются нечётными, поэтому обойти все мосты, побывав на каждом ровно один раз, нельзя.

Многие, наверное, знакомы со следующей «детской» задачей. Можно ли нарисовать домик, не отрывая ручки от бумаги?

В данном случае ответ положительный, т.к. число нечётных вершин равно 2. Только начинать и заканчивать обход нужно обязательно в вершине нечётной степени.

Другой очень известной задачей теории графов является проблема 4-х красок. Суть её состоит в следующем. На плоскости имеется географическая карта, на которой нанесены страны со своими границами. Всегда ли хватит четырёх красок, чтобы раскрасить эту карту таким образом, чтобы любые две граничащие страны были раскрашены в разные цвета? Каждая страна, естественно, окрашивается в один цвет. То, что число красок должно быть не меньше четырёх, показывает, например, следующая карта.

Эта проблема стояла около 100 лет и была окончательно разрешена относительно недавно (в 1976 году) американскими математиками Хакеном и Аппелем при существенном использовании вычислительной техники.

3.2. Графы. Основные понятия

Определение 1. Пусть – некоторое множество, называемое в дальнейшем множеством вершин,– множество всех его двухэлементных подмножеств. Пусть– некоторое подмножество в, называемое в дальнейшем множеством рёбер. Тогда параназывается простым графом или просто графом. Эту пару мы часто будем обозначатьили просто.

Если , то вершиныбудем называть концами ребра. Будем также говорить, что вершины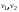инцидентны ребруили реброинцидентно вершинами. Вершины, соединённые ребром, будем называть соседними, а рёбра, инцидентные одной и той же вершине, смежными.

В некоторых случаях рассматривают графы, в которых две фиксированные вершины могут быть соединены не одним ребром, а несколькими. Могут также рассматриваться графы с «петлями», т.е. с рёбрами вида . Такие графы мы пока рассматривать не будем.

Мы будем рассматривать только конечные графы, т.е. множество вершин 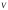всегда предполагается конечным.

Пример 1. Рассмотрим граф , где,. Его можно изобразить с помощью следующего рисунка.

Однако его можно изобразить и по-другому.

Разные рисунки представляют один и тот же граф. В связи с этим важным является понятие изоморфизма графов.

Определение 2. Графы иназываются изоморфными, если существует такое взаимно однозначное отображение

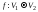
что любые две вершины соединены ребром в графе тогда и только тогда, когда их образы соединены ребром в графе, т.е.

.

Теперь несложно убедиться, что все нарисованные выше графы изоморфны.

Важной характеристикой графа является группа его автоморфизмов. Она отражает меры симметрии этого графа.

Определение 3. Пусть имеется граф . Изоморфизмы графав себя называются автоморфизмами. Все автоморфизмы графа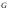образуют группу, которая называется группой автоморфизмов графаи обозначается.

Пример 2. Найдём группу автоморфизмов следующего графа

Можно произвольным образом перенумеровать вершины графа и среди всех перестановок вершин выбрать те, которые удовлетворяют определению изоморфизма графов.

Допустим, мы перенумеровали вершины таким образом:

Тогда автоморфизмами графа будут следующие перестановки

.

Как известно, существуют две группы из четырёх элементов и обе они абелевы. Это 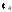и. Поскольку порядки получившихся автоморфизмов не более 2, то

.

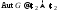Определение 4. Маршрутом в графе называется последовательность вершин и рёбер, начинающаяся и заканчивающаяся вершиной.

Маршрут, в котором все рёбра разные, называется цепью. Цепь, в которой все вершины разные, называется простой цепью.

Определение 5. Цепь, в которой первая и последняя вершины совпадают, называется циклом. Цикл, в котором все вершины кроме первой и последней разные, называется простым циклом.

Определение 6. Граф 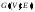называется подграфом графа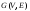, если, причём оба конца любого ребра издолжны принадлежать.

Определение 7. Граф называется связным, если каждая пара его вершин соединена цепью.

Определение 8. Пусть – произвольный граф. Тогда множество его вершинможно разбить на такие непересекающиеся подмножества, что любые две вершины из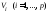соединены цепью и никакая вершина изне соединена цепью ни с какой вершиной из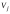при.

Пусть обозначает множество всех рёбер из, оба конца которых принадлежат. Тогда подграфыназываются компонентами связности графа.

Пример 3. Граф, изображённый на рисунке, имеет 3 компоненты связности

Определение 9. Граф называется полным, если любые его две вершины соединены ребром. Полный граф навершинах обозначается.

Пример 4. Граф .
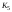