
Задачи.
Докажите, что следующие булевы функции тождественно равны, сравнив их таблицы истинности.
1.  .
.
2.  .
.
3.  .
.
4. 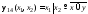 .
.
Для следующих булевых функций трёх переменных составьте их таблицы истинности.
5.  .
.
6.  .
.
7.  .
.
Найдите СДНФ и СКНФ для следующих функций.
8. Для
функции
 .
.
9. Для
функции
 .
.
10. Для
функции
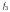 .
.
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
4.3. Полные системы и замкнутые классы булевых функций
Определение
1.
Пусть
 – некоторая система булевых функций
произвольного конечного числа аргументов,
а
– некоторая система булевых функций
произвольного конечного числа аргументов,
а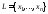 – фиксированный набор переменных.
Определим множество функций
– фиксированный набор переменных.
Определим множество функций ,
порождённое системой
,
порождённое системой .
Пусть
.
Пусть .
Будем считать, что функция, которая
получается в результате подстановки
вместо аргументов функции
.
Будем считать, что функция, которая
получается в результате подстановки
вместо аргументов функции переменных из списка
переменных из списка (в любых сочетаниях), принадлежит
(в любых сочетаниях), принадлежит .
Кроме того, если функция
.
Кроме того, если функция ,
то функция, полученная в результате
подстановки вместо аргументов функции
,
то функция, полученная в результате
подстановки вместо аргументов функции любых переменных из списка
любых переменных из списка или функция из
или функция из ,
также принадлежит
,
также принадлежит .
Будем говорить, что множество функций
.
Будем говорить, что множество функций порождено системой
порождено системой .
Функцию, принадлежащую
.
Функцию, принадлежащую ,
будем называть суперпозицией функций
из
,
будем называть суперпозицией функций
из .
.
Определение
2.
Система
булевых функций
 называется полной, если для любого
списка конечного числа переменных
называется полной, если для любого
списка конечного числа переменных множество
множество совпадает с множеством всех булевых
функций
совпадает с множеством всех булевых
функций переменных.
переменных.
Определение
3.
Полная
система булевых функций
 называется базисом, если она является
минимальной полной системой по включению.
Другими словами, если из этой системы
удалить хотя бы одну функцию, то оставшиеся
функции уже не будут образовывать полную
систему.
называется базисом, если она является
минимальной полной системой по включению.
Другими словами, если из этой системы
удалить хотя бы одну функцию, то оставшиеся
функции уже не будут образовывать полную
систему.
Лемма.
Пусть
имеются две системы
 и
и ,
и каждая из функций системы
,
и каждая из функций системы выражается через функции системы
выражается через функции системы .
Тогда, если система
.
Тогда, если система является полной, то и система
является полной, то и система будет полной.
будет полной.
Доказательство.
Пусть
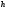 – произвольная булева функции. Тогда
её можно выразить через функции системы
– произвольная булева функции. Тогда
её можно выразить через функции системы .
Каждую функцию, входящую в это выражение
можно в свою очередь выразить через
функции системы
.
Каждую функцию, входящую в это выражение
можно в свою очередь выразить через
функции системы .
В результате получим выражение функции
.
В результате получим выражение функции через функции системы, следовательно,
эта система также является полной.
через функции системы, следовательно,
эта система также является полной.
Лемма доказана.
Теорема 1. Следующие системы булевых функция являются полными:
(А):
 ;
;
(В):
 ;
;
(С):
 ;
;
(D):
 .
.
Доказательство.
Из теоремы 1 предыдущего параграфа
следует, что система
 является полной. Но
является полной. Но .
Поэтому система (А) полна.
.
Поэтому система (А) полна.
Аналогично,
полна система (B),
поскольку
 .
Далее,
.
Далее, .
Поэтому
.
Поэтому .
Кроме того,
.
Кроме того, .
Значит, система (С) также полна.
.
Значит, система (С) также полна.
Аналогично полна система (D).
Теорема доказана.
Определение
3.
Если
в качестве сложения рассматривать
сложение по модулю 2 (обозначение
 ),
а в качестве умножения – конъюнкцию
(обозначение
),
а в качестве умножения – конъюнкцию
(обозначение ),
то многочлен от
),
то многочлен от переменных с коэффициентами 0 и 1
называется многочленом Жегалкина.
переменных с коэффициентами 0 и 1
называется многочленом Жегалкина.
Заметим,
что в многочлене Жегалкина не могут
присутствовать степени переменных выше
первой, поскольку всегда
 .
.
Теорема 2. Каждая булева функция может быть записана в виде многочлена Жегалкина, причём, единственным образом.
Доказательство.
Во-первых, заметим, что система функций
 является полной, поскольку
является полной, поскольку .
Следовательно, любую булеву функцию
можно записать в виде многочлена
Жегалкина.
.
Следовательно, любую булеву функцию
можно записать в виде многочлена
Жегалкина.
Подсчитаем
число многочленов Жегалкина от
 переменных. Число одночленов есть
переменных. Число одночленов есть .
Перед каждым из них можно поставить
коэффициент 0 или 1 и образовать сумму.
В итоге получим
.
Перед каждым из них можно поставить
коэффициент 0 или 1 и образовать сумму.
В итоге получим многочленов, т.е. ровно столько же,
сколько и булевых функций. Поскольку
разные булевы функции не могут иметь
один и тот же многочлен Жегалкина, то
соответствие между многочленами
Жегалкина и булевыми функциями является
взаимно однозначным.
многочленов, т.е. ровно столько же,
сколько и булевых функций. Поскольку
разные булевы функции не могут иметь
один и тот же многочлен Жегалкина, то
соответствие между многочленами
Жегалкина и булевыми функциями является
взаимно однозначным.
Теорема доказана.
Пример.
Запишем дизъюнкцию
 в виде многочлена Жегалкина.
в виде многочлена Жегалкина. .
.
Определение
4.
Семейство
булевых функций
 будем называть замкнутым классом, если
любая суперпозиция функций из
будем называть замкнутым классом, если
любая суперпозиция функций из опять принадлежит
опять принадлежит .
.
Определение
5.
Класс
всех булевых функций (любого конечного
числа аргументов), для которых
 ,
обозначим
,
обозначим .
Класс всех булевых функций, для которых
.
Класс всех булевых функций, для которых ,
обозначим
,
обозначим
 .
.
Предложение
1.
Классы
 и
и являются замкнутыми.
являются замкнутыми.
Доказательство.
Пусть
 и
и
 .
Заметим, что
.
Заметим, что ,
поэтому возможно, что
,
поэтому возможно, что .
Тогда
.
Тогда и, значит, класс
и, значит, класс замкнут.
замкнут.
Аналогично,
 замкнут.
замкнут.
Предложение доказано.
Определение
6.
Функция
 называется двойственной к
называется двойственной к .
В случае
.
В случае функция
функция называется самодвойственной. Класс
всех самодвойственных функций обозначим
называется самодвойственной. Класс
всех самодвойственных функций обозначим .
.
Предложение
2.
Класс
 замкнут.
замкнут.
Доказательство.
Заметим, что
 .
Пусть
.
Пусть
 ,
, ,…,
,…,

и
 .
.
Тогда


 ,
,
что
и означает самодвойственность функции
 .
.
Предложение доказано.
Определение
7.
Будем
считать, что две двоичные последовательности
длины

 и
и связаны неравенством
связаны неравенством ,
если
,
если .
Функцию
.
Функцию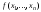 будем называть монотонной, если для
любых наборов
будем называть монотонной, если для
любых наборов и
и ,
таких что
,
таких что выполняется неравенство
выполняется неравенство .
Класс всех монотонных функций обозначим
.
Класс всех монотонных функций обозначим .
.
Предложение
3.
Класс
 замкнут.
замкнут.
Доказательство.
Заметим, что
 .
Пусть
.
Пусть
 .
.
Подставим
функцию
 в
в вместо переменной
вместо переменной .
Возьмём наборы
.
Возьмём наборы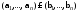 .
Пусть
.
Пусть ,
, .
Тогда
.
Тогда и
и

 ,
,
что
и означает замкнутость
 .
.
Предложение доказано.
Определение
8.
Булеву
функцию
 переменных будем называть линейной,
если она имеет вид
переменных будем называть линейной,
если она имеет вид
 ,
где
,
где
 .
.
Предложение
4.
Класс
 всех линейных функций замкнут.
всех линейных функций замкнут.
Доказательство.
Если
 и
и ,
то, подставляя в
,
то, подставляя в эти выражения, мы получим снова линейную
функцию.
эти выражения, мы получим снова линейную
функцию.
Предложение доказано.
Предложение
5.
Классы
 различны.
различны.
Доказательство.
Составим таблицу принадлежности функций
 этим классам (принадлежность обозначается
+).
этим классам (принадлежность обозначается
+).
|
|
|
|
|
|
|
|
0 |
+ |
– |
– |
+ |
+ |
|
1 |
– |
+ |
– |
+ |
+ |
|
|
– |
– |
+ |
– |
+ |
Так как все столбцы различны, то все классы разные.
Предложение доказано.
Заметим
также, что каждый из классов
 не совпадает с множеством всех булевых
функций.
не совпадает с множеством всех булевых
функций.












