
4. Элементы математической логики
4.1. Алгебра высказываний
Одним из первоначальных понятий математической логики является понятие высказывания. В математике мы часто имеем дело с различными высказываниями. Например,
 ;
;17 делится на 8;
101 – простое число.
Каждое такое высказывание формулируется с помощью математических символов или слов какого-то языка. Мы можем сказать, что первое и второе высказывания из этого списка являются, очевидно, ложными, а третье высказывание – истинно. Высказывание – это такое предложение, формулируемое с помощью некоторого языка, относительно которого имеет смысл говорить истинно оно или ложно. Не каждую последовательность математических символов или слов некоторого языка можно считать высказыванием. Например, следующие предложения высказываниями не являются.
Число 0,0001 очень мало.
Существует ли число, квадрат которого равен 2?
Да здравствует книга – источник знаний!
 .
.
Действительно,
в первом предложении понятие очень мало
не имеет точного смысла, и поэтому мы
не можем сделать вывода о справедливости
такого утверждения. Не имеет смысла
говорить истинно или ложно вопросительное
или восклицательное предложение. Что
касается последнего, то, не зная
 ,
мы не можем сказать истинно это неравенство
или нет.
,
мы не можем сказать истинно это неравенство
или нет.
Относительно высказываний справедливо следующее:
всякое высказывание является либо истинным, либо ложным (закон исключения третьего);
никакое высказывание не может быть одновременно истинным и ложным (закон противоречия);
Каждому высказыванию мы будем сопоставлять его значение истинности: 1 – если высказывание истинно, и 0 – если ложно.
В
дальнейшем высказывания мы будем обычно
обозначать большими латинскими буквами:
 .
.
Над высказываниями можно производить логические операции. Мы рассмотрим следующие из них: конъюнкцию, дизъюнкцию, отрицание, импликацию, эквивалентность. Результатом операции над высказываниями является новое высказывание. Дать определение операции означает в точности указать, когда новое высказывание является истинным, а когда – ложным. Определение вышеназванных операций мы дадим чуть ниже с помощью так называемой таблицы истинности, а пока приведём их обозначение и соответствующий им оборот русского языка.
|
Название операции |
Обозначение |
Оборот русского языка |
|
1. Конъюнкция |
|
«и» |
|
2. Дизъюнкция |
|
«или» |
|
3. Отрицание |
|
«не» |
|
4. Импликация |
|
«если
|
|
5. Эквивалентность |
|
« |
В следующей таблице указаны значения истинности полученного в результате операции высказывания в зависимости от значений истинности высказываний, участвующих в операции. Её можно рассматривать как определение этих операций.
Определение 1.
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Для
примера сформулируем определение
конъюнкции. Конъюнкцией двух высказываний
 и
и называется высказывание, которое истинно
только в том случае, когда истинны оба
высказывания
называется высказывание, которое истинно
только в том случае, когда истинны оба
высказывания и
и одновременно.
одновременно.
Аналогично, пользуясь вышеприведённой таблицей, можно сформулировать определения остальных логических операций.
Пример
1.
 – идёт дождь,
– идёт дождь,
 – дует ветер.
– дует ветер.
 –идёт
дождь и дует ветер;
–идёт
дождь и дует ветер;
 –идёт
дождь или дует ветер;
–идёт
дождь или дует ветер;
 –дождь
не идёт;
–дождь
не идёт;
 –если
идёт дождь, то дует ветер;
–если
идёт дождь, то дует ветер;
 –дождь
идёт тогда и только тогда, когда дует
ветер.
–дождь
идёт тогда и только тогда, когда дует
ветер.
В
дальнейшем мы будем отвлекаться от
конкретного смысла высказывания
 и считать
и считать просто переменной, принимающей два
значения: 0 или 1. Такие переменные
называют логическими или булевыми.
просто переменной, принимающей два
значения: 0 или 1. Такие переменные
называют логическими или булевыми.
Теперь перейдём к предикатам.
Определение 2. Если некоторое предложение содержит переменные величины, принимающие значения из некоторого множества так, что при каждом наборе конкретных значений этих величин данное предложение превращается в высказывание, то мы имеем дело с предикатом. Количество неизвестных величин, входящих в такое предложение, называется местностью предиката. Бывают одноместные, двухместные, трёхместные и т.д. предикаты.
Приведём некоторые примеры.
Пример 2.
 ;
; ;
; делится
на 6;
делится
на 6; делится
на
делится
на
 ;
; .
.
Уравнение
 из 1) содержит переменную
из 1) содержит переменную .
При подстановке конкретных значений
.
При подстановке конкретных значений мы получаем высказывание, которое может
быть верным или неверным. Так, при
мы получаем высказывание, которое может
быть верным или неверным. Так, при получаем неверное равенство
получаем неверное равенство ,
а при
,
а при – верное
– верное .
.
Для
каждого предиката нужно знать, какие
значения могут принимать неизвестные
величины. Так, в 1), 2) и 5) неизвестные
 и
и могут принимать действительные значения,
а в 3) и 4) неизвестные
могут принимать действительные значения,
а в 3) и 4) неизвестные и
и предполагаются натуральными числами.
Предикаты в 1), 2), 3) – одноместные. В 4) и
5) мы имеем дело с двухместным и трёхместным
предикатами соответственно.
предполагаются натуральными числами.
Предикаты в 1), 2), 3) – одноместные. В 4) и
5) мы имеем дело с двухместным и трёхместным
предикатами соответственно.
Далее,
к предикатам мы будем приписывать так
называемые кванторы. Бывают квантор
всеобщности (обозначение
 )
и квантор существования (обозначение
)
и квантор существования (обозначение ).
).
Обозначение
 читается « для любого
читается « для любого ».
Обозначение
».
Обозначение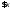 читается « существует
читается « существует ».
К любой неизвестной величине, входящей
в предикат, можно слева приписать
квантор. Если к
».
К любой неизвестной величине, входящей
в предикат, можно слева приписать
квантор. Если к -местному
предикату слева приписать квантор,
относящийся к одной из неизвестных, то
получится
-местному
предикату слева приписать квантор,
относящийся к одной из неизвестных, то
получится -местный
предикат.
-местный
предикат.
Пример 3.
 ;
; ;
; делится
на 6;
делится
на 6; делится
на
делится
на
 ;
; ;
; .
.
Запишем
словесно, например, последнее высказывание:
«Для любого
 и для любого
и для любого существует такое
существует такое ,
что
,
что .
.
В
заключение отметим, как можно построить
отрицание высказывания, содержащего
кванторы. Пусть
 – одноместный предикат с неизвестным
– одноместный предикат с неизвестным .
Отрицание высказывания
.
Отрицание высказывания означает, что
означает, что верно не для всех
верно не для всех ,
т.е. существует такое
,
т.е. существует такое ,
для которого
,
для которого неверно. Поэтому
неверно. Поэтому
 .
.
Аналогично,
 .
.
Пример 4.


 .
.





 ,
то
,
то »,
«из
»,
«из следует
следует »
»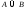
 тогда и только тогда,
когда
тогда и только тогда,
когда »
»





