2. Элементы теории кодирования

2.1. Линейные коды

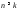Пусть имеется канал связи, по которому передаётся двоичная информация. Если двоичная последовательность разбивается на блоки длины , которые в соответствии с процедурой кодирования преобразуются в блоки длины, то такое кодирование называется блочным.

Пример 1. Одним из наиболее простых линейных кодов является код проверки на чётность. Двоичная последовательность длиныпреобразуется в двоичную последовательностьдлины, где. Код проверки на чётность позволяет обнаруживать одиночную ошибку. Если в полученном сообщении, это свидетельствует о наличии, по крайней мере, одной ошибки (или нечётного числа ошибок).

Определение 1. Линейным -кодом будем называть линейное подпространстворазмерностив линейном пространстве.

Определение 2. Если , то весом Хэммингавекторабудем называть число его ненулевых координат. Если, то числобудем называть расстоянием между векторамии.

Определение 3. Число будем называть весом кодаи обозначать.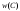

Определение 4. Матрицу размера, строки которой составлены из координат векторовнекоторого базиса кодабудем называть порождающей матрицей кода.

Определение 5. Пусть– элементы пространства. Величину

назовём их псевдоскалярным произведением. В случае элементыибудем называть ортогональными. Если– линейное подпространство в, тобудем называть ортогональным дополнением для.

Очевидно, – само является линейным подпространством. Из курса линейной алгебры известно, что сумма размерностей подпространствиравна.

Заметим, что возможно для, т.е. не выполнена одна из аксиом скалярного произведения. Поэтому произведениемы называем псевдоскалярным.

Определение 6. Пусть – ортогональное дополнение кодав пространстве. Кодназывается двойственным к, а его порождающая матрицаразмераназывается проверочной матрицей кода. Очевидно,.

Пример 2. Пусть процедура кодирования состоит в том, что двоичной последовательности длины 3 сопоставляется двоичная последовательностьдлины 5 по формулам

,

.

Тогда код есть множество решений этой системы линейных однородных уравнений ранга 2 с пятью неизвестными. Следовательно, кодимеет размерность 3. Фундаментальную систему решений можно выбрать из векторов

,

,

.

Порождающая матрица кода , таким образом, имеет вид

.

Ортогональным кодом будем множество решений систему уравнений

,

,

.

Фундаментальная система решений имеет вид

,

.

Таким образом, проверочная матрица кода есть

.

Код есть линейный (5, 3)-код.

Путём переименования переменных и линейных преобразований над строками матрицывсегда можно добиться, чтобы проверочная матрица имела бы вид, где– единичная подматрица. В нашем примере. Порождающая матрица может быть задана в виде.

Связь между проверочной и порождающей матрицей даёт

Предложение 1. Если – проверочная матрица-кода, то– его порождающая матрица.

Наоборот, если – порождающая матрица кода, то– его проверочная матрица.

Доказательство. Нужно лишь проверить, что .

Предложение 2. Вес линейного -кодаравенлюбыестолбцов проверочной матрицы линейно независимы, но некоторыестолбцов линейно зависимы.

Доказательство. . Допустим противное. Пусть столбцы с номерамилинейно зависимы. Тогда, взяв векторс единицами на указанных местах и нулями на остальных, получим, что. Но тогда– кодовое слово с весом, меньшим. Противоречие.

. Любой вектор веса меньше не может быть кодовым словом, и существует векторвеса, являющийся кодовым словом.

Предложение доказано.

Следствие. .

Доказательство. Число линейно независимых столбцов не превосходит числа строк матрицы . Поэтому.

Предложение 3. Линейный код обнаруживаетошибоквес кода.

Линейный код исправляетошибоквес кода.

Доказательство. Действительно, если вес кода равен 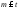, то найдутся два кодовых словаи, расстояние между которыми равно. Тогда, сделавошибок, возможно, мы вместо кодового слована приёме получим слово. Но тогда, получив кодовое слово, у нас не будет оснований утверждать наличие ошибок. Если же вес кода не менее чем, то при наличии не болееошибок на приёме мы не получим кодового слова и, таким образом, сможем констатировать наличие ошибок.

Далее. Пусть . Если, то множествоназовём шаром радиусас центром в точке. Очевидно, что если, то шарыине могут пересекаться. Поэтому, если в словесделано не более чемошибок, то полученное словоостанется в шареи мы его декодируем как, т.е. ошибки будут исправлены. Если же, то некоторые шарыимогут пересекаться и тогда словопосле того, как в нём сделаноошибок, может попасть в шар, и в этом случае мы не сможем его правильно декодировать.

Предложение доказано.

Общая процедура декодирования линейного кода состоит в следующем. Если имеется линейный-код, то абелеву группумы раскладываем в смежные классы по подгруппе. В каждом смежном классе выбираем слово наименьшего веса. Если в данном смежном классе несколько слов наименьшего веса, выбираем любое из них. Выбранное слово называется лидером. Если на приём поступило слово, и это слово содержится в-м смежном классе, то мы декодируем его как. Таким образом, данный код будет исправлять в точности те ошибки, которые совпадают с лидерами смежных классов.

Пример 2 (продолжение). Разложение абелевой группы по подгруппеимеет следующий вид

Лидеры смежных классов расположены в первой строчке. Допустим, что на вход поступает слово . Сначала оно кодируется как. Предположим, что при передаче по каналу связи во втором разряде была допущена ошибка, и на приёме получено слово. Это слово содержится в четвёртом смежном классе, поэтому при декодировании к нему прибавляется лидер этого смежного класса:. В результате мы получаем слово, которое после отсечения последних двух разрядов будет равно. Таким образом, ошибка исправлена.

Для того чтобы исправить одну ошибку, можно действовать и по-другому. Если умножить проверочную матрицу на вектор, то получится слово. Оно называется синдромом и равно тому столбцу проверочной матрицы, в котором допущена ошибка. В данном случае словосовпадает со вторым столбцом матрицы, поэтому в словенужно исправить второй разряд.

Заметим, что если бы ошибка произошла на первом или третьем разрядах, то слово было бы декодировано неправильно. Это свидетельствует о том, что данный код ещё очень мало эффективен в плане исправления ошибок. Далее мы познакомимся с более эффективными кодами.