
Основы дискретной математики
.pdf
подмножеством T0 (первый столбец таблицы заполнен только плюсами), то система неполна. В противном случае переходим к классу T1 и т.д.
Пример 3. Используя критерий полноты, выяснить, полна ли система булевых функций B:
а) B = {xy z, x ↔ y, x y} ;
б) B = {x ↔ y, x} .
◄ а) Для удобства рассуждений зададим функции системы B таблично (табл. 2.30 и 2.31).
Таблица 2.30 |
Таблица 2.31 |
x |
y |
z |
xy |
f1 = xy z |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
x |
y |
f2 = x ↔ y |
f3 = x |
|
|
y |
|
||||
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
Заполним таблицу Поста исследуемой системы (табл. 2.32).
|
|
|
|
|
|
|
Таблица 2.32 |
Класс T0 : f1 (0, 0, 0) = 0 , следовательно, f1 T0 ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
f2 (0, 0, 0) =1 , следовательно, f2 T0 . Выяснять, |
||
Функции |
|
|
Классы Поста |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
T0 |
|
T1 |
|
S |
|
M |
|
L |
принадлежит или нет классу T0 функция f3 , не надо, |
|||
|
|
|
|
|
|
|
|
||||||
f1 = xy z |
|
+ |
|
+ |
|
– |
|
+ |
|
– |
так как в системе уже нашлась функция, не |
||
f2 = x ↔ y |
|
– |
|
+ |
|
|
|
– |
|
|
принадлежащая T0 . |
||
f3 = x |
|
|
|
|
|
– |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
Класс T1 : f1 (1,1,1) = 1, следовательно, f1 T1 ; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 (1,1,1) =1 , следовательно, |
f2 T1 ; f3 (1,1,1) = 0 , следовательно, f3 T1 . |
||||||||||||
Класс S : f |
= (01010111) , |
f * = (00010101) , следовательно, f S . |
|||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|||
PDF created with pdfFactory Pro trial version www.pdffactory.com

Класс M : перебрав все пары сравнимых векторов, убеждаемся, что условие монотонности для функции f1 не нарушается, значит, f1 ÎM ; (0,0) p (0,1) , а f2 (0, 0) > f2 (0,1) , следовательно, f2 ÏM .
Класс L : f1 = xy Ú z = xy Å z Å xyz , следовательно, f1 ÏL .
Таким образом, для каждого класса Поста можно указать функцию системы B,емуне принадлежащую. Следовательно, B - полная система.
б) Заполним таблицу Поста системы B (табл. 2.33). |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
Таблица 2.33 |
Класс T0 : f1 (0, 0) =1, следовательно, f1 Ï T0 . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Класс T1 : f1 (1,1) = 1, следовательно, f1 Î T1 ; f2 (1,1) = 0 , |
||||
Функции |
|
|
Классы Поста |
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
следовательно, f2 Ï T1 . |
|
|
|
||||
|
T0 |
|
T1 |
|
S |
|
M |
|
L |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
f1 = x « y |
|
– |
|
+ |
|
– |
|
– |
|
+ |
Класс S : f = (1001) , |
f * = (0110) , следовательно, f ÏS . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
||
f2 = |
|
|
|
|
|
– |
|
|
|
|
|
|
+ |
|
|
|
|
|
x |
|
|
|
|
|
|
|
Класс M : (0,0) p (0,1) |
, f1 |
(0, 0) > f1(0,1) , следовательно, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f1 ÏM . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Класс L : |
f1 = x « y = |
|
|
= 1Å x Å y , следовательно, f1 ÎL ; |
f2 = |
|
=1Å x , следовательно, |
|||||||||||
x Å y |
x |
|||||||||||||||||
f2 ÎL . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку обе функции системы B принадлежат классу линейных функций, то система неполна. ►
Упражнение |
|
2 |
.30. |
Используя критерий |
полноты, выяснить, полна ли система |
|||||
булевых функций B: |
|
|
{ |
|
} |
|||||
|
{ |
|
|
} |
|
|
|
|
||
а) B = |
|
x ® y, xy |
z |
|
; |
|
б) B = |
|
z Ú xy,1, 0 . |
|
Определение. Полная система функций называется базисом, если после удаления из нее любой функции получается неполная система.
Пример 4. Укажите подмножества B, являющиеся базисами:
а) B = {x Ú y, xy, x} ; б) B = {xy Ú z, x « y, x y} .
◄ а) Заполним таблицу Поста (табл. 2.34).
PDF created with pdfFactory Pro trial version www.pdffactory.com

Для каждого класса Поста можно указать функцию |
|
|
|
|
|
|
|
|
|
Таблица 2.34 |
|||||||||||||||||||||||||||
системы, которая ему не принадлежит (для T0 , T1 и |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Классы Поста |
|
||||||
M это x , для S и L это x y |
( xy )), значит, система |
|
|
Функции |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
{x y, xy, |
|
} полная. При этом анализ табл. 2.34 |
|
|
|
T0 |
|
T1 |
S |
M |
|
L |
|||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
x y |
|
+ |
|
+ |
|
– |
+ |
|
– |
||||||||||||||||||||||||||
показывает, что эта система базисом не является, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
xy |
|
+ |
|
+ |
|
– |
+ |
|
– |
||||||||||||||||||||||||||
поскольку не теряет полноты при удалении x y или |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
– |
|
– |
+ |
– |
|
+ |
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
. Полученные в результате удаления этих функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
множества {x y, |
|
|
} |
и {xy, |
|
|
} |
являются базисами, так как полны и при удалении из них |
|
||||||||||||||||||||||||||||
x |
x |
|
|||||||||||||||||||||||||||||||||||
любой из функций полноту теряют ( x y T0 , xy T0 , |
|
L ). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
б) Мы рассматривали систему B = {xy z, x ↔ y, x |
|
} в примере 3. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Таблица 2.35 |
|
Чтобы выделить из этой полной системы базисы, |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
заполним таблицу Поста системы B полностью (табл. |
|||||||||||||||||
Функции |
|
|
|
|
Классы Поста |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
2.35). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
T0 |
|
T1 |
|
|
|
S |
|
M |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ табл. 2.35 показывает, что сама система B |
|
|||||||||||||||||||||||
f1 = xy z |
|
|
|
+ |
+ |
– |
+ |
– |
|
|
|||||||||||||||||||||||||||
|
|
|
|
базисом не является, так как при удалении функции |
|
||||||||||||||||||||||||||||||||
f2 = x ↔ y |
|
|
|
– |
+ |
– |
– |
+ |
|
|
|||||||||||||||||||||||||||
|
|
|
|
xy z полноту не теряет. Система |
{x ↔ y, x |
|
} |
является |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||||||||
f3 = x |
|
|
|
+ |
|
– |
|
|
|
– |
|
– |
|
|
– |
|
|
||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
базисом, поскольку удаление из нее любой из функций |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
приводит к потере полноты. Остальные собственные подмножества B базисами не являются (система {xy Ú z, x « y} неполная, так как лежит в T1 ; система {xy z, x y}
неполная, так как лежит в T0 ; неполны и подмножества, содержащие по одной функции). ►
Упражнение 2.31. Указать подмножества B, являющиеся базисами:
|
{ |
|
} |
|
{ |
|
} |
|
а) B = |
|
x Å y, 0,1, xy ; |
б) B = |
|
x |
↓ y, x |
y . |
|
|
|
|
|
Теоретические обоснования |
||||
Лемма о функции, не сохраняющей 0. Пусть f T0 . Тогда формулой над |
||||||||
множеством { f } |
можно задать либо константу 1, либо отрицание. |
|||||||
Доказательство. Пусть |
f T0 , т.е. f |
(0, 0,..., 0) =1. Отождествим между собой все |
||||||
переменные функции f . Получим функцию от одной переменной j(x) = f (x, x,..., x) .
Возможны два случая: f (1,1,...,1) = 0 или f (1,1,...,1) =1 .
PDF created with pdfFactory Pro trial version www.pdffactory.com
В первом случае |
f (0, 0,..., 0) =1 и f |
(1,1,...,1) = 0 , следовательно, |
ϕ(0) = 1 и ϕ(1) = 0 , откуда |
|||||||||||||||||||||||
j(x) = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Во втором случае |
f (0, 0,..., 0) =1 и |
f (1,1,...,1) =1 , следовательно, ϕ(0) = 1 и ϕ(1) = 1, откуда |
||||||||||||||||||||||||
ϕ(x) = 1.■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Лемма о функции, не сохраняющей 1. Пусть f T1 . Тогда формулой над |
|
|
|
|
||||||||||||||||||||||
множеством { f } |
можно задать либо константу 0, либо отрицание. |
|
|
|
|
|||||||||||||||||||||
Доказательство. Пусть f T1 , т.е. f (1,1,...,1) = 0 . Отождествим между собой все |
|
|||||||||||||||||||||||||
переменные функции f . Получим функцию от одной переменной j(x) = f (x, x,..., x) . |
|
|||||||||||||||||||||||||
Возможны два случая: f (0, 0,..., 0) = 0 или f (0,0,...,0) = 1 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
В первом случае |
f (0, 0,..., 0) = 0 и f |
(1,1,...,1) = 0 , следовательно, |
|
|
|
|
|
|
|
|
|
|||||||||||||||
ϕ(0) = 0 и ϕ(1) = 0 , откуда ϕ(x) = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Во втором случае |
f (0, 0,..., 0) =1 и |
f (1,1,...,1) = 0 , следовательно, ϕ(0) = 1 и ϕ(1) = 0 , откуда |
||||||||||||||||||||||||
j(x) = |
|
.■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
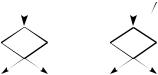
На рис. 2.1 и 2.2 представлены условные обозначения |
|
|
|
|
f C T0 |
|
|
f C T1 |
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
алгоритмов, использованных при доказательствах |
_ |
|
_ |
|
||||||||||||||||||||||
|
T0 |
T1 |
|
|||||||||||||||||||||||
леммы о функции, не сохраняющей 0, и леммы о |
_ |
0 |
|
|
_ |
|||||||||||||||||||||
функции, не сохраняющей 1. |
1 |
|
|
|
|
x |
|
|
x |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Лемма о несамодвойственной функции. Пусть |
Рис. 2.1. |
Рис. 2.2. |
||||||||||||||||||||||||
f (x1, x2 ,..., xn ) - несамодвойственная функция. Тогда |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
формулой над множеством { f , Ø} |
можно задать константы 0 и 1. |
|
|
|
|
|||||||||||||||||||||
Доказательство. Пусть f S . Тогда существует набор (a1, a2 ,..., an ) значений |
|
|||||||||||||||||||||||||
переменных (x1, x2 ,..., xn ) , такой что f (a1, a2 ,..., an ) ¹ |
|
|
|
|
|
|
|
|
|
|
|
, и, значит, |
|
|||||||||||||
f ( |
|
|
, |
|
|
,..., |
|
) |
|
|||||||||||||||||
a1 |
a2 |
an |
|
|||||||||||||||||||||||
|
|
|
|
|
f (α1, α2 ,..., αn ) = f ( |
|
, |
|
,..., |
|
). |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
α1 |
α2 |
αn |
|
|
|
|
|
|
|
|
|
||||||||||||
Рассмотрим функцию j(x) = f (xα1 , xα2 ,..., xαn ), где xαi = x , если αi = 0 , и xαi |
= x , если |
|
||||||||||||||||||||||||
αi = 1 . Заметим, что 0αi = |
|
, 1αi = αi . |
|
|
|
|
|
|
|
|
|
|||||||||||||||
αi |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, f C S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
j(0) = f (0α1 , 0α2 ,..., 0αn ) = f (a1, a2 ,..., an ) |
; |
|||||||||||||||
_ |
||||||||||||||||
j(1) = f (1α1 ,1α2 ,...,1αn )= f (a1, a2 ,..., an ) . |
|
S |
||||||||||||||
|
|
0, 1 |
||||||||||||||
|
|
|||||||||||||||
С учетом равенства |
|
|
||||||||||||||
|
|
|
||||||||||||||
f (a1, a2 ,..., an ) = f ( |
|
, |
|
,..., |
|
) |
|
Рис. 2.3. |
||||||||
a1 |
a2 |
an |
|
|||||||||||||
получим j(0) = j(1) , т.е. j(x) - константа, j(x) - другая константа. ■
На рис. 2.3 представлено условное обозначение алгоритма, использованного в доказательстве леммы о несамодвойственной функции.
Лемма о немонотонной функции. Пусть f (x1, x2 ,..., xn ) - немонотонная функция.
Тогда формулой над множеством { f , 0,1} можно задать отрицание.
Доказательство. Пусть f ÏM . Тогда существуют такие наборы (a1, a2 ,..., an ) и (b1,b2 ,...,bn ) значений переменных, что (a1,a2,...,an ) p (b1,b2,...,bn ), а
f (a1, a2 ,..., an ) > f (b1,b2 ,...,bn ) , и, значит, f (a1, a2 ,..., an ) =1 , f (b1,b2 ,...,bn ) = 0 .
Поскольку (a1, a2 ,..., an ) ¹ (b1,b2 ,...,bn ) , то можно выделить подпоследовательность индексов 1 £ i1 < i2 < ... < ik £ n такую, что ai1 = bi1 , ai2 = bi2 , ..., aik = bik и для всякого
i ¹ i1, i2 ,..., ik ai ¹ bi (и, значит, ai = 0, bi = 1 ).
Рассмотрим функцию j(x) , заданную формулой, полученной в результате подстановки в формулу f (x1, x2 ,..., xn ) вместо переменных xi1 , xi2 ,..., xik чисел ai1 , ai2 ,..., aik соответственно, а на остальные места - x . Не ограничивая общности рассуждений, можно считать, что
|
|
j(x) = f (x,..., x,ai |
, x,..., x,ai , x,..., x,...,ai |
, x,..., x) . |
|||
|
|
|
1 |
|
2 |
k |
|
Так как ai = 0 |
при i ¹ i1,...,ik , имеем |
|
|
|
|
||
|
j(0) = f (0,...,0,ai ,0,...,0,ai |
,0,...,0,...,ai |
,0,...,0) = f (a1,a2 ,...,an ) = 1 . |
||||
|
|
1 |
2 |
|
k |
|
|
Так как bi = 1 |
при i ¹ i1 |
,...,ik и ai |
= bi , …, ai |
= bi |
, имеем |
|
|
|
|
1 |
1 |
k |
k |
|
|
|
j(1) = f |
(1,...,1,ai ,1,...,1,ai |
,1,...,1,...,ai |
,1,...,1) = f |
(b1,b2 ,...,bn ) = 0 . |
||
|
|
1 |
2 |
|
k |
|
|
Равенства j(0) = 1 и j(1) = 0 означают, что j(x) = x . ■
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
0,1, f C M |
На рис. 2.4 представлено условное обозначение алгоритма, |
|
||
_ |
использованного при доказательстве леммы о немонотонной функции. |
|
M |
||
|
|
|
|
_ |
|
|
x |
|
Рис. 2.4.
Лемма о нелинейной функции. Пусть f ÏL . Тогда формулой над множеством
{ f , 0,1, x} можно задать конъюнкцию.
Доказательство. Пусть f ÏL . Тогда в каноническом полиноме Жегалкина данной функции найдется член с отличным от нуля коэффициентом, содержащий произведение переменных. Не нарушая общности рассуждений, можно считать, что этот член содержит x1 × x2 . Следовательно, полином Жегалкина функции f можно
преобразовать к виду
f = x1x2 × f1 (x3 , x4 ,..., xn )Å x1 × f2 (x3 , x4 ,..., xn )Å
Åx2 × f3 (x3 , x4 ,..., xn )Å f4 (x3 , x4 ,..., xn ) ,
где функция f1 такова, что найдется набор (s3 , s4 ,..., sn ) значений переменных такой,
что f1 (s3 , s4 ,..., sn ) ¹ 0 .
Рассмотрим функцию j(x1, x2 ) = f (x1, x2 , s3 , s4 ,..., sn ), или
j(x1, x2 ) = x1x2 × f1 (s3,s4 ,...,sn ) Å x1 × f2 (s3,s4 ,...,sn ) Å
Åx2 × f3 (s3,s4 ,...,sn ) Å f4 (s3,s4 ,...,sn ) =
= x1x2 Å ax1 Å bx2 Å g ,
где a = f2 (s3,s4 ,...,sn ) , b = f3 (s3,s4 ,...,sn ) , g = f4 (s3,s4 ,...,sn ) .
Теперь рассмотрим функцию f(x1, x2 ) , получаемую из функции j(x1, x2 ) следующим образом:
f(x1, x2 ) = j(x1 Å b, x2 Å a) Å ab Å g .
Преобразуем формулу, реализующую функцию f(x1, x2 ) :
f(x1, x2 ) = (x1 Åb)×(x2 Åa)Åa (x1 Åb)Åb(x2 Åa)Å Åg Å abÅ g = x1x2 Åbx2 Å x1a Åba Å ax1 Å ab Å Åbx2 Åba Å g Å ab Å g = x1x2 .
PDF created with pdfFactory Pro trial version www.pdffactory.com

Подытоживая проделанное, можем записать
x1x2 = f (x1 Åb, x2 Å a, s3 , s4 ,..., sn ) Å ab Å g .
Заметим, что
|
ìx , если b = 0; |
|
ìx |
|
, если a = 0; |
ì f , |
если ab Å g = 0; |
||||||
|
ï |
1 |
|
|
ï |
2 |
|
|
ï |
|
|
|
|
x Åb = í |
|
|
x Å a = í |
|
|
|
, если a = 1, |
f Å ab Å g = í |
|
|
если ab Å g = 1. |
||
1 |
ï x , если b = 1, |
2 |
ï x |
2 |
ï f , |
||||||||
|
î |
1 |
|
|
î |
|
|
î |
|
|
|
||
|
|
0,1, x , f C L Таким образом, можно утверждать, что конъюнкция x x |
2 |
реализована |
|
|
|||
|
|
|||
_ |
1 |
|
||
|
|
|
||
L |
формулой над множеством { f , 0,1, x} .■ |
|
xy
На рис. 2.5 представлено условное обозначение алгоритма,
использованного при доказательстве леммы о нелинейной функции.
Рис. 2.5.
Теорема 2.13 (критерий полноты Поста). Для того чтобы система функций B = { f1,..., fk } была полна, необходимо и достаточно, чтобы для каждого из классов Поста в B нашлась функция fi , ему не принадлежащая.
Доказательство. Необходимость. Пусть система B полна. Надо доказать, что для каждого из классов Поста найдется функция fi , ему не принадлежащая.
Рассуждаем от противного: предположим, что найдется класс Поста (обозначим его D ), в котором содержатся все функции из B. Тогда
(B Ì D) Þ ([B] Ì [D]) |
Þ (P2 Ì D) . |
|
т.к. Bполна, |
|
а D замкнут |
Следовательно, (P2 D) (D P2 ) . т.е. D = P2 . Но этого не может быть, поскольку есть булевы функции, не принадлежащие ни одному из классов Поста (например, штрих Шеффера). Получили противоречие, следовательно, наше предположение было неверным.
Достаточность. Пусть найдутся функции f0 , f1, fS, fM, fL из B такие, что f0 ÏT0 , f1 Ï T1 , fS ÏS , fM ÏM , fL Ï L . Покажем, что отрицание и конъюнкцию можно реализовать формулами над множеством { f0 , f1, fS, fM, fL} . Схема построения соответствующих формул представлена на рис. 2.6.
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
|
|
|
|
|
|
|
|
f0C T0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
T0 |
|
|
|
|
|
|
|
|||
|
f1 |
C |
T1 |
1 |
|
|
|
x |
T1 |
f1 |
C |
T1 |
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
T |
|
fLC L |
|
|
|
|
|||||||
fM |
C M 0,1 |
|
|
|
x |
|
|
|
fS C S |
||||||||||
0,1, x |
|
|
|
0,1, x |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
S |
||||||
|
|
|
|
|
0,1, x |
|
|
|
|
0,1, |
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
L |
|
|
|
|
||||||||
 xy, x
xy, x
Рис. 2.6.
Таким образом, конъюнкцию и отрицание можно задать формулой над B. Имеем:
система {x, xy} полная, и каждая ее функция может быть выражена формулой над B.
Следовательно, условия теоремы о полноте двух систем выполнены и, значит, B - полная система. ■
Задачи повышенной сложности
2.34.Используя теорему о полноте двух систем, доказать, что {x ↓ y} полная система.
2.35.Опираясь на доказательство леммы о функции, не сохраняющей 0, реализовать формулой над множеством f = (10010000) либо 1, либо отрицание.
2.36.Опираясь на доказательство леммы о функции, не сохраняющей 1, реализовать формулой над множеством f = (00010000) либо 0, либо отрицание.
2.37.Опираясь на доказательство леммы о несамодвойственной функции, реализовать формулой над множеством {(01101011), x} константы 0 и 1.
2.38.Опираясь на доказательство леммы о немонотонной функции, реализовать формулой над множеством {(01101011), 0,1} отрицание.
2.39.Опираясь на доказательство леммы о нелинейной функции, реализовать формулой над множеством {(11100100), 0,1} конъюнкцию.
PDF created with pdfFactory Pro trial version www.pdffactory.com
2.40.Доказать, что из любой полной системы можно выделить полную подсистему, содержащую не более пяти функций.
2.41.Доказать, что всякий замкнутый класс функций, не совпадающий с P2 ,
содержится, по крайней мере, в одном из классов Поста.
2.42. Назовем систему булевых функций предполным классом, если эта система неполна и добавление к ней любой функции, ей не принадлежащей, приводит к образованию полной системы. Доказать, что:
а) классы Поста являются предполными;
б) других предполных классов, кроме классов Поста, нет.
2.43. Доказать, что во всяком базисе содержится не более четырех функций.
PDF created with pdfFactory Pro trial version www.pdffactory.com

Глава 3. Теория графов
§ 3.1. Основные определения
Граф, его вершины и ребра. Смежные вершины. Кратные ребра, петли. Инцидентные вершины и ребра. Степени вершин. Висячие и изолированные вершины. Лемма о рукопожатиях. Диаграмма графа. Изоморфные графы. Специальные виды графов: обыкновенные, полные, двудольные, полные двудольные графы. Матрица смежности и матрица инцидентности. Подграф. Операции над графами: объединение, пересечение, декартово произведение.
Базовые понятия и утверждения
1. Общие понятия. Различают два вида графов - неориентированные и ориентированные. Знакомство с теорией графов мы начнем с изучения графов первого вида.
Определение. Пусть V - конечное непустое множество, E - конечное множество, состоящее из поименованных неупорядоченных пар элементов множества V , причем это могут быть пары из одинаковых элементов и одинаковые пары с разными именами. Совокупность множеств V и E называют графом (или неориентированным графом) и
обозначают G = (V , E) .
Элементы множества V называют вершинами, а элементы множества E - ребрами.
Граф может вовсе не иметь ребер. Такой граф называют нулевым.
Множества вершин V и ребер E графа G также обозначают V (G) и E(G)
соответственно. Если ребро e - это пара вершин vi и vj , то пишут e = vi vj .
Обычно графы представляют диаграммами. Каждой вершине графа vi ставят в соответствие свою точку плоскости или пространства, которую помечают тем же символом, что и вершину vi , а каждому ребру e = vi vj ставят в соответствие непрерывную кривую, соединяющую точки vi , vj и не проходящую через точки,
изображающие другие вершины графа.
PDF created with pdfFactory Pro trial version www.pdffactory.com
