тральных колес и др. (см. ниже). В передачах с плавающими звеньями KH = 1,1 - 1,3; без компенсирующих устройств KH = 1,5 - 2.

Радиальные и осевые усилия определяются по окружным так же, как в простых зубчатых передачах.

КПД планетарных передач и указания к выбору схемы

Потери мощности в планетарном редукторе складываются из по- терь на трение в подшипниках, потерь на разбрызгивание и перемеши- вание масла, а также потерь в зубчатых зацеплениях. При этом потери в зацеплениях зависят от схемы редуктора и передаточного числа.

КПД планетарной передачи определяется по формулам: при ведущем колесе 1:

трение в зацеплениях и подшипниках. Для планетарных передач в силу некоторой специфики их работы можно принять ψ13H = 0,01 - 0,001.

КПД планетарного редуктора существенно зависит от схемы ре- дуктора и передаточного числа. При выборе схемы планетарной переда-

чи для получения удовлетворительного КПД следует придерживаться приведенных ниже рекомендаций.

Для планетарной передачи по схеме рис.1,а i1H = 3 - 8 при высоком КПД η13H = 0,96 - 0,99. Для передачи по схеме рис.1,б i13H =1,3 - 1,6 так

же при высоком КПД η13H = 0,96 - 0,99. Однако вторая передача более

сложная по конструкции, чем первая.

Высокие передаточные числа могут быть получены в передачах по схеме рис.1,в, г: iH3 1 ≤ 1600 . Однако в этом случае получается низкий КПД (рис.3). Рациональными считаются передаточные отношения

7

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

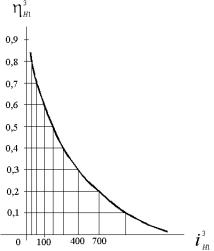
iH31 = 25 - 100 . При этом η3H1 = 0,9 - 0,65 (меньшие значения для

больших передаточных отношений). Эти схемы рекомендуется исполь- зовать в кинематических механизмах.

Рис.3. Зависимость КПД от передаточного отношения

Для силовых передач, где КПД имеет существенное значение, при больших передаточных отношениях лучше использовать после- довательное соединение передач по схеме рис.1,а.

Выбор чисел зубьев колес

При проектировании планетарного редуктора передаточное отно-

шение i13H или iH3 1 бывает задано. Числа зубьев колес определяют по

заданному передаточному отношению в соответствии со схемой меха- низма по формулам (2) - (5).

При этом следует учитывать ряд условий.

1. Если зубчатые колеса нарезаются без смещения инструмента, то число зубьев у колеса с внешними зубьями должно быть больше 17 (из условия отсутствия подреза). Во внутреннем зацеплении сателлита и колеса с внутренними зубьями должны соблюдаться ограничения, при- веденные в табл.1 [1].

8

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

2. Условие соосности центральных колес требует равенства межосевых расстояний зубчатых пар редуктора:

для схемы рис.1,а:

Если условие (12) трудно выполнить при одинаковом модуле обеих ступеней, то можно назначить разные модули для каждой ступени. Из этих же соображений одну из ступений (обычно с внешним зацеплени- ем) можно делать косозубой (более подробно для каждой схемы см. ниже).

3. Условие сборки или симметричного размещения сателлитов проверяется после назначения числа сателлитов (обычно С принимают равным трем). Оно всегда выполняется, если числа зубьев центральных

где γ и δ - целые числа.

Для схем с двухвенцовым сателлитом, конструкция которых до-

пускает изменение положения венцов друг относительно друга при монтаже колес, при обеспечении сборки достаточно удовлетворить только условиям соосности и соседства.

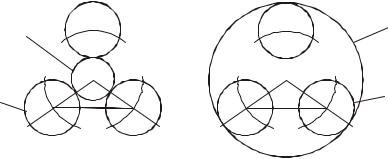
4. Условие соседства состоит в том, что для обеспечения зазора между сателлитами сумма радиусов окружностей вершин соседних са- теллитов должна быть меньше расстояния между их осями (рис.4).

9

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

зубьев центральных колес 1 и 3.

Минимальное расстояние между сателлитами принимают равным 0,5m, где m - модуль зацепления.

Если выполнить все эти условия при заданном передаточном от- ношении затруднительно, допускается отклонение передаточного от- ношения u = ±4% .

Расчет планетарных передач на прочность

Планетарные передачи рассчитывают на изгибную и контактную прочность зубьев по формулам для простых зубчатых передач [2]. При этом учитывают разветвление потока мощности между сателлитами.

При проектном расчете закрытых планетарных передач, работаю- щих в масляной ванне, определяют диаметр меньшего из колес рассчи- тываемой зубчатой пары из условия контактной прочности зубьев:

10

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Здесь T1 - крутящий момент на меньшем из колес рассчитываемой зуб- чатой пары ( Н ×м ); u - передаточное число зубчатой пары, определяе- мое как отношение большего числа зубьев к меньшему. Если в паре центральное колесо - сателлит меньшим оказывается сателлит, то мо- мент T1 определяется делением известного момента на центральном

колесе на передаточное число u; Ybd = bw 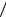d1 - коэффициент ширины венца относительно диаметра; bw - ширина зубчатого венца. При про- ектном расчете принимают Ψbd £ 0,75 .

В выражении (16) С - число сателлитов; KHβ - коэффициент кон- центрации нагрузки, выбираемый в зависимости от величины Ψbd (см. табл.1.6 в [2], как при консольном расположении колес); sHP - допус- каемое контактное напряжение для материала колеса (выбор материа- лов и допускаемых напряжений см. [2]), МПа; Kd = 780 - для стальных прямозубых колес; Kd = 680 - для стальных косозубых колес. Знак "+" в

формуле относится к внешнему зацеплению, знак " -" - к внутреннему.

Можно также определить межосевое расстояние передачи по формуле

где ψba = 2uψ±bd1 .

Рекомендации по выбору Ψbd см. выше; Ka = 495 - для стальных прямозубых колес; Ka = 430 - для стальных косозубых колес. Все остальные величины имеют те же значения и размерности, что и в формуле (16).

Так как зубчатые пары в редукторе имеют одинаковые межосевые расстояния, то расчет ведут обычно для одного из зацеплений. Для схе- мы рис.1,а это внешнее зацепление (внутреннее зацепление в этом слу- чае является более прочным).

11

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com