Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЧМ_Лекции2009.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

1.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Лекция 9.

Решение СЛАУ трехдиагонального вида методом прогонки.

Рассмотрим разностное уравнение

	Ai yi−1 −Ci yi + Bi yi+1 = −Fi							(1)
	i =1, 2,...		Ai ≠ 0,	Bi ≠ 0		(для определенности)
Поскольку	y′′(x)	i =	yi+1 − 2yi + yi−1		+O(h		2	) , то ясно, что это разностное

			h2

уравнение соответствует определенному дифференциальному уравнению второго порядка.

Для решения (1) необходимо задать 2 дополнительных условия. Если оба условия (например, значения функции y0 и первой разности y0 = y1 − y0 или,

что то же самое, y0 и y1 ) заданы в одной точке, то получаем задачу Коши.

Если же дополнительные условия заданы в разных точках (не соседних), то полученная задача называется краевой.

Например,				y0 = μ1 ;	yN = μ2 .
Для задачи Коши заданы y0 и							y0 = y1 − y0 (или y0 и y1 ) , тогда
y	i+1	=	Ci yi − Ai yi−1 − Fi		,	B ≠ 0 .

				Bi		i

В этом случае задача разрешима и притом единственным образом.
Но для уравнений					второго порядка МФ наиболее характерны, типичные
краевые задачи.
Например,				при i = 0 задано y0 ,			и при i = N задано yN , требуется найти yi ,
0 <i < N , если y0 =μ1 и yN = μ2 , где μ1,μ2 - заданные числа.
Множество точек (узлов)						i = 0,1, 2,...N называется сеткой. В граничных уз-
лах сетки i = 0				и i = N	могут быть заданы не только значения функции, но и

значения первой разности или линейная комбинация функции и первой разности.

Общий вид условий можно записать в виде:

y0 = χ1 y1 + μ1, yN = χ 2 yN −1 + μ2 .

(2)

Подставляя	y1 = y0 + y0 , первое из условий (2) перепишем в виде
χ1 y0 −(1− χ1) y0 = μ1 .
Случай χ1 = 0	означает, что в граничном узле i = 0 задано значение функ-

ции y0 (граничное условие первого рода, или граничное условие Дирихле).

Если χ1 =1, то задано значение y0 (граничное условие второго рода).

В случае χ1 ≠ 0 и χ1 ≠1 в точке i = 0 задана линейная комбинация функции и первой разности (граничное условие третьего рода).

Итак, основной интерес представляют краевые задачи. Большое достижение вычислительной математики состоит в том, что для огромного количества задач математической физики вычисления строятся таким способом, что на каждом шаге приходится решать трехточечные уравнения (1) с граничными условиями (2). Эта задача является классической, к ней сводятся многие сложные задачи теории вычислительных методов. Матрица такой системы уравнений является трехдиагональной. Она имеет вид:

	1	−χ	1	0 ...	0	0	0 ...	0		0		0
			1	B1 ...
A1		−C1		B1 ...	0	0	0 ...	0		0		0
...		... ... ... ...				... ... ...		...		...		...
													, Ay = F . (3)
A =	0	0		0 ...	Ai	−Ci	Bi ...	0		0		0	, Ay = F . (3)
		... ... ... ...				... ... ...		...		...		...
...		... ... ... ...				... ... ...		...		...		...
	0	0		0 ...	0	0	0 ...	A	−C	N −1	B	N −1
								N −1		N −1		N −1
	0	0		0 ...	0	0	0 ...	0	−χ2			1

Ее порядок равен N +1 . Во всех случаях от нуля отличны только коэффициенты, стоящие на трех диагоналях: главной и двух соседних.

Для решения систем линейных уравнений с матрицей такого типа очень эффективен метод Гаусса, который приводит в данном случае к формулам, которые принято называть формулами прогона.

				Действительно,					применим к системе уравнений Ay = F , где
							μ	1
		y				−		1
		y	0			−	F
			0			−		1
y =		y				−	F		, простейшую схему исключения Гаусса (без выбора
y =			1	,	F =		2		, простейшую схему исключения Гаусса (без выбора
	...						...
						− F
	y					− F
			N				N −1
							μ2
							μ2

главного элемента).

Умножим первое уравнение на A1 и вычтем из второго уравнения. В ре-

			y1 = α2 y2 +β2
зультате исключим из второго уравнения	y	:	y	2	= α	3	y	3	+β	3
	1			2		3		3		3
					...
					...

итоге

приходим

системе с

двухдиагональной

матрицей:

yi = αi+1 yi+1 +βi+1;

= χ2 yN −1 +μ2 ;

i =1,2,..., N −1.

Из последних двух урав-

нений вычислим yN и после этого обратным ходом все yi , i = N −1,...,1 .

Итак, идея решения получена. Теперь более подробно.

Пусть имеет место рекуррентное соотношение

yi = αi+1 yi+1 +βi+1,

(*)

неопределенными

коэффициентами

αi

и βi . Тогда

выражение

yi−1 = αi yi

+βi подставим в формулу Ai yi−1 −Ci yi + Bi yi+1 = −Fi

(*)

и полу-

чим

(Aiαi −Ci ) yi + Aiβi

+ Bi yi+1 = −Fi

(**).

Воспользуемся теперь соотношением (*). В результате получим:

((Aiαi −Ci )αi+1 + Bi ) yi+1 + Aiβi + (Aiαi −Ci )βi+1 = −Fi .

Это

уравнение

должно

быть

выполнено

для

любых

поэтому

(Aiαi −Ci )αi+1 + Bi = 0 ; Aiβi +(Aiαi −Ci )βi+1 = −Fi .

Отсюда получаем рекуррентные формулы для αi и βi :

αi+1 =

;

βi+1 =

Aiβi + Fi

;

i =1,2,..., N −1 .

(4)

Ci −αi Ai

Начальные значения α1 и β1

можно найти из левого граничного условия:

y0 = α1 y1 +β1

= χ

+μ

1 1

отсюда α1 = χ1,

β1 =μ1 .

Таким образом,

по формулам (4) при

i =1,2,..., N −1 , т.е.

слева направо,

можно вычислить все значения коэффициентов

αi

и βi

по αN

и βN

(формулы

прямой прогонки).

После того,

как коэффициенты αi и βi

найдены, можно воспользоваться

граничными условиями справа, т.е.

yN −1 = αN yN +βN

yN = χ2 yN −1 +μ2


отсюда, исключая yN −1 , вычисляется yN	=	μ2 + χ2βN		.

		1−αN χ2
Таким образом, для вычисления значений			yi получаем формулы “справа
налево”, т.е. формулы обратной прогонки:	yi		= αi+1 yi+1 +βi+1 , i = N −1,...,1. Изло-
женный метод называется методом прогонки (или правой прогонки).

Соберем все формулы правой прогонки и запишем их в порядке использования:

→ αi+1			=	Bi	;	i =1,2,..., N −1;	α1 = χ1
→ αi+1			=	Ci −αi Ai	;	i =1,2,..., N −1;	α1 = χ1
				Ci −αi Ai
→β	i+1		=	Aiβi + Fi	;	i =1,2,..., N −1;	β = μ	1
→β			=		;	i =1,2,..., N −1;	β = μ
				Ci −αi Ai			1
				Ci −αi Ai
yN =		μ2 + χ2βN
yN =		1−αN χ2
		1−αN χ2
← yi		= αi+1 yi+1 +βi+1 ,				i = N −1,...,1,0 .
Стрелки указывают направление счета:								→ от i к i +1
								← от i +1 к i .

Количество арифметических операций M =8N , т.е. пропорционально числу узлов сетки. Это достигается за счет того, что не выполнялись операции с нулевыми элементами.

Определение. Методы, в которых число действий пропорционально количеству узлов, называются экономичными.

Устойчивость метода прогонки.

Все формулы прогонки были выведены формально. Мы делили на выражения Ci −αi Ai и 1−αN χ2 , не зная, можно ли это делать. Сформулируем доста-

точные условия, при которых написанные формулы имеют смысл:

≥

, i =1,2,..., N −1 (диагональное пре-

обладание)

χα

≤1,

α =1,2.

χ1

χ2

< 2 .

Можно легко показать, что при этих условиях

αi

≤1,

i =1,2,..., N.

В этом случае

δyi

≤

αi+1

δyi+1

≤

δyi+1

Таким образом, счет по формулам прогонки устойчив, погрешность от шага к шагу не нарастает.

Упражнение. Доказать, что погрешность от шага к шагу не нарастает.

Предположим, что

αi

≤1. Покажем, что

αi+1

≤1.

Заметим, что

α1

χ1

≤1.

Рассмотрим разность

Ci −αi Ai

−

≥

−

αi

−

≥

(1−

αi

) ≥ 0 .

Поскольку Bi ≠ 0 , то

Ci −αi Ai

> 0 , т.е.

αi+1

≤1.

Ci −

αi Ai

Отсюда видно, что

αi+1

<1 , если

αi

<1;

все

αi

<1 при

α1

χ1

≤1.

Отметим, что если

хотя бы в одной точке, то i >i0 :

αi

<1 и

αN

<1. В этом случае условие

χ1

χ2

< 2 является лишним, т.к. 1−

αn

χ2

> 0 .

Таким

образом,

при

выполнении

достаточных

условий

≥

, i =1,2,..., N −1 ;

χα

≤1,

α =1,2 ;

χ1

χ2

< 2

задача имеет

единст-

венное решение, т.к.

αi

≤1, то счет устойчив

δyi

≤

αi+1

δyi+1

≤

δyi+1

Рассмотрим теперь модельную краевую задачу

ξy′′+ y′ = 0

ξ <1 .

= 0, y(1) =1

y(0)

Данное уравнение имеет точное аналитическое решение:

y = eλx ,	ξλ2 + λ = 0 ;	λ = 0,	λ		= −	1
						ξ
		1		2

y(x) = C1 +C2 exp − ξx .

C1 +C2 = 0−1

C1 +C2e ξ =1

Точное решение:

	1					1
	1					1

y =		−	1	1−exp	−	ξ x	.
	1−exp	−	1
			ξ
			ξ

Уравнение типа пограничного слоя (малый параметр при старшей производной) (Рис. 9.1):

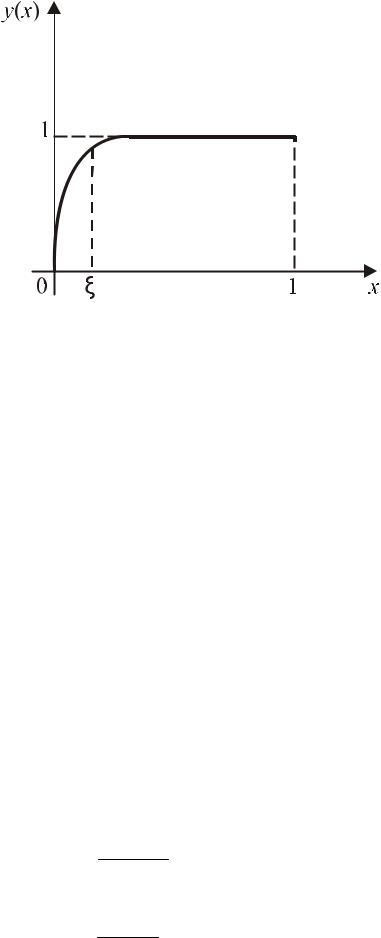
Рис. 9.1 График функции, являющейся решением уравнения

Функция y(x) быстро меняется от 0 до своего значения в центре области

на толщине пограничного слоя x = ξ.	Если ξ	мало, то важно, сколько узлов
сетки попадает в пограничный слой.	От этого зависит		точность решения в
этой области.
Введем на x [0;1] сетку x = x0 + mh,	x0 = 0;	m = 0,1,..., M ;	Mh =1 .

По формулам численного дифференцирования, разлагая функцию y(x) в

ряд Тейлора в окрестности произвольного узла xm , получим

′

′′

′′′

+O(h

)

(1)

ym+1 = ym + ym h

′

′′

′′′

+O(h

(2)

ym−1 = ym − ym h

−

)

′′

получим формулу 2-го порядка аппроксимации:

Отсюда для ym

′′

ym−1 −2 ym + ym+1

+O(h

) .

ym =

Для первой производной ym′ возможны различные формы записи: 1. центральная разность (из (1) вычесть (2))

ym′ = ym+12−hym−1 +O(h2 )

2. разность вперед (из формулы (1))

ym′ = ym+1h− ym +O(h)

3. разность назад (из формулы (2))

ym′ = ym −hym−1 +O(h) .

В итоге получаем семейство трех разностных схем, при одинаковой аппроксимации второй производной и при одинаковых граничных (краевых) условиях:

ym+1 − ym−1

− 2 y

+ y

m−1

m+1

− y

= 0; m =1,2,..., M −1 ; y0

= 0,

yM =1. (3)

ym − ym−1

Аппроксимация РС №1 исходной краевой задачи есть O(h2 ) ;

Аппроксимация РС №2 и РС №3 исходной краевой задачи есть O(h) , т.к.

если хотя бы одно слагаемое и хотя бы в одном узле аппроксимировано O(h) ,

то и аппроксимация всей РС есть O(h) . Задачу (3) можно решить методом про-

гонки, т.к. это система трех точечных уравнений.

Am ym−1 −Cm ym + Bm ym+1 = 0 ;

m =1,2,..., M −1 ;

μ1 = 0 ; μ2 =1 ;

χ1 = χ2 = 0 .

Достаточное условие устойчивости прогонок:

≥

i =1,2,..., N −1 .

Условия χi <1 выполнены.

Для центральной разности первой производной РС №1

2ξ

;

A =

−

;

Если подставить это в (*), то получим

2ξ

≥

−

;

−

≥

−

отсюда

−

≥ 0

или h ≤ 2ξ .

Для разности вперед получаем условие РС №2 устойчивости – устойчива

Для разности назад получаем условие устойчивости h < ξ

Итак, РС №1 и РС №3 условно устойчивы, т.е. при выполнении некоторого условия на h : h ≤ 2ξ и h < ξ. РС №2 безусловно устойчива, т.е. при любом

h .

Но кроме условия устойчивости необходимо выполнение условия аппроксимации.

При O(h) , например, при h = 401 погрешность C 401 , а при O(h2 ) погреш-

ность C 16001 .

Это очень большая разница.

Кроме того, совершенно недостаточно, чтобы в РС №1 было h ≤ 2ξ или в РС №2 h < ξ. Как видно их характера решения, которое очень сильно изменя-

ется в диапазоне от 0 до ξ (см. рис.), в диапазоне x [0;ξ] желательно распо-

ложить не 1, а 2-3-4 узла сетки, поскольку основная погрешность решения возникает именно в этом диапазоне быстрого изменения решения ( ξ - погра-

ничный слой).

Рассмотрим другой подход к анализу устойчивости РС. Аналитическое решение

y =

1−exp

−

ξ x

1−exp−

При

малом

его

можно описать следующим образом

−

y0 =1;

y = y0 + y0 ;

= −e

Здесь y0

- решение, соответствующей вырожденной задачи

0 y0′′ + y0′ = 0;

y0 (1) =1

y0 (x)=1,

погранслойная поправка,

назначение которой состоит в

а функция y0

том, чтобы удовлетворять левому граничному условию.

Для анализа линейных однородных РС, также как и для анализа линейных однородных ДУ, применим метод Эйлера:

на сетке xm = mh положим ym = eλxm = eλmh = qm , где q = eλh .

Подставляя ym = qm в РС №1 с центрально-разностной аппроксимацией, и,

сокращая на qm−1 ≠ 0 , получим характеристическое уравнение для определения

q :

q2 − 2q +1

q2 −1

= 0 .

Отсюда q1 =1; q2 =

−1

1−

2ξ

Общее решение y

= C +C

qm .

Условие устойчивости h < 2ξ .

Частное

решение

(приближенно, аналогично непрерывному случаю)

Um =1− q2m ;

если

q2 ≥ 0 , то

ym с ростом m монотонно изменяется от 0 до 1; если

q2 < 0 , то изменение немонотонное (Рис. 9.2).

Рис. 9.2 Иллюстрация нарушения условия устойчивости

Для РС №2 (разность вперед первой производной)


ξ	ym−1 − 2 ym + ym+1	+	ym+1 − ym		= 0;
	h2
				h
имеем ym = eλmh = qm ,				q = eλh .

q2 −2q +1

q2 − q

= 0

q =1;

Частное решение ym ≈1− q2m , эта функция всегда монотонная. При измене-

нии ξ эта функция качественно ведет себя также, как и аналитическое реше-

ние: чем меньше ξ , тем больше знаменатель в q2 и тем быстрее затухает по-

гранслойная поправка. Это вполне согласуется с безусловной устойчивостью прогонок для РС №2.

На самом деле в пограничный слой желательно поместить 2-3-4 узла, иначе именно в этом месте резкого изменения функции погрешность будет наиболее значительной.

Для РС №3:

ym−1 − 2 ym + ym+1

ym − ym−1

= 0;

ym = eλmh = qm ,

q = eλh .

q2 − 2q +1

q −1

= 0

q =1;

=1−

;

Частное решение ym ≈1− q2m , при h > ξ нарастание немонотонное, условие устойчивости h < ξ.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.06.2015529.41 Кб28ЦИС лр № 1.doc
#
05.06.2015375.3 Кб10ЦИС лр № 2.doc
#
05.06.2015371.71 Кб11ЦИС лр № 4.doc
#
05.06.2015179.19 Кб17Число_состояний_электрона.docx
#
25.09.20194.03 Mб60ЧМ_8 на листе A4.doc
#
05.06.20151.42 Mб19ЧМ_Лекции2009.pdf
#
05.06.201548.13 Кб13Шаблон договора на практику.doc
#
27.03.20169.82 Mб3107Шилдт c++_базовый_курс издание 3.pdf
#
29.08.20193.7 Mб15Шпора ИПУ часть 2.doc
#
18.12.2018291.46 Кб7шпора ооиб.docx
#
27.08.20193.15 Mб25Шпора_МПСС.docx