
Лекция 3.
Приближение функций интерполяционными полиномами.
Пусть функция f (x) задана множеством своих значений для дискретного
набора точек:
x |
|
x0 |
x1 |
|
… |
|
xn |
|
|
|
|
|
|
|
|
f (x) |
|
f0 |
f1 |
|
… |
|
fn |
|
|
|
|
|
|
|
|
здесь |
fi = f |
(xi ) |
|
|
|
|
|
Требуется найти приближенное значение |
f (x) для |
x ≠ xi . Это одна из са- |
|||||
мых часто встречающихся прикладных задач. (Табличные значения могут быть получены либо в результате расчетов, проведенных на компьютере, либо в процессе замеров, осуществленных в рамках какого-либо эксперимента.)
Очевидно, что для достаточно подробной таблицы (когда xi − x - малые величины), для x ≈ xi можно положить f (x)≈ fi .
Погрешность этого приближения |
′ |
f (x)− fi ≈ f (x) (x − xi ). |
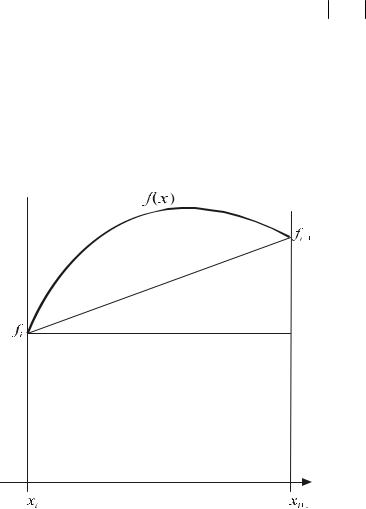
Наверное, более точное приближение получим, если для x [xi , xi+1 ] заме-
ним функцию f (x) отрезком прямой проходящим через точки(xi , fi ), (xi+1 , fi+1 ),
как это показано на (Рис. 3.1):
Рис.3.1 Линейная интерполяция |
19

f (x)≈ fi + fi+1 − fi (x − xi ) xi+1 − xi
Таким образом, возникает идея приближения функции степенными полиномами, принимающими в заданных точках заданные (табличные) значения. Эта идея лежит в основе интерполирования.
Итак, пусть функция f (x) задана таблицей:{fi = f (xi ), i = 0,1,2,..., n}, содер-
жащей значения в (n +1)точке, причем xi попарно различные.
Будем искать полином отx , проходящий через табличные точки:
Pn (x)= a0 + a1 x + a2 x2 +... + an xn (1)
Требуя, чтобы в каждой табличной точке значение полинома совпадало с заданным значением функции, получим замкнутую систему линейных уравнений относительно неопределенных коэффициентов{ak }:
ao + a1 xi + a2 xi2 +... + an xin = fi ; i = 0,1,..., n
Определителем этой системы является рассматриваемый в курсе математического анализа определитель Вандермонда для системы несовпадающих точек:
|
1 |
x0 |
x02 |
... |
x0n |
= ∏n (xi − x j )≠ 0 |
= |
1 |
x1 |
x12 |
... |
x1n |
|
|
... ... |
... |
... |
... |
i, j=0 |
|
|
1 |
xn |
xn2 |
... |
xnn |
(i≠ j) |
т.е. искомый полином существует и единственен.
Замечательно то, что решение поставленной задачи можно сразу выписать в явном виде:
P |
(x)= f |
|
|
|
|
(x − x1 )(x − x2 )...(x − xn ) |
|
+... |
+ f |
|
|
|
|
|
(x − x0 )...(x − xk −1 )(x − xk +1 )...(x − xn ) |
|
|
+ |
|||||||||||||||||||||||||||||||||||
|
|
|
|
) |
|
|
(x |
|
|
|
) |
||||||||||||||||||||||||||||||||||||||||||
n |
|
0 |
|
(x |
0 |
− x |
)(x |
0 |
− x |
2 |
)...(x |
0 |
− x |
n |
|
|
|
k |
|
|
|
k |
− x |
0 |
)...(x |
k |
− x |
k −1 |
)(x |
k |
− x |
k +1 |
)...(x |
k |
− x |
n |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
(x − x |
0 |
)(x − x )...(x − x |
n−1 |
) |
|
|
n |
|
|
|
|
|
L(k )(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
+... + fn |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
= ∑ fk |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(x |
n |
− x |
0 |
)(x |
n |
− x )...(x |
n |
− x |
n−1 |
) |
|
|
|
(k ) |
(xk ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
где L(k )(x)= |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
k =0 |
|
|
|
Ln |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(x − x |
0 |
)(x − x |
)...(x − x |
k −1 |
)(x − x |
k +1 |
)...(x − x |
n |
) - |
|
|
полиномы |
n -ой |
степени |
|
|
|||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
специального вида. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
В самом деле, очевидно, что |
|
|
Pn (x) представляет собой полином n -ой |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
степени и что при подстановке в него значения x = xk получим Pn (xk )= fk |
k . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
20

Полином, |
|
проходящий через табличные |
точки и записанный в форме |
|||||||
n |
L(k )(x) |
|
|
|
||||||
Pn (x)= ∑fk |
|
n |
|
|
|
|
(2) , называется интерполяционным полиномом Лагранжа. |
|||
|
(k ) |
(x |
|
) |
||||||
k =0 |
L |
|
k |
|
|
|
||||
n |
|
|
|
|
|
|
|
|||
Значения {xi ;i = 0,1,..., n} называют узлами интерполяции. |
|
|||||||||
Если узлы упорядочить по величине, т.е. |
xi+1 > xi |
i , то величины |
||||||||
{hi = xi+1 − xi ; |
|
i = 0,1,..., n −1} называют шагами интерполяции. |
|
|||||||
Еслиh = hi |
= const , так что xi = x0 +ih,i = 0,1,..., n , то говорят об интерполяции |
|||||||||
по равноотстоящим узлам.
Не следует думать, что для каждой непрерывной функции f (x), x [a;b],
интерполяционный многочлен, построенный по значениям в равноотстоящих
Упражнение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Показать, |
что |
для |
функции f (x)= |
|
1 |
, f (x) C ∞ [a;b], |
при |
|||||||
|
+ 25x2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
x0 = a = −1; xn = b =1 |
отклонение |
max |
|
f (x)− Pn (x) |
|
|
не стремится к 0 с ростом n . |
|||||||
|
|
|||||||||||||
|
|
|
−1≤x≤1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Введем в рассмотрение еще один полином специального вида (n +1) |
сте- |
|||||||||||||
пени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
||||||
ωn+1 (x)= (x − x0 )(x − x1 )...(x − xn )= ∏(x − xi ) |
|
|
|
|
|
|||||||||
|
|
|
i=0 |
|
|
|
|
|
||||||
Тогда, L(nk )(xk )= ω′n+1 (xk ), |
гдеL(nk ) = |
ωn+1 (x) |
; |
и поэтому полином Лагранжа |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
x − xk |
|
|
|
|
|
|||
можно записать с использованием ωn+1(x) в виде:
Pn (x)= ωn+1 (x) ∑n ω′n+1 (xk f)k (x − xk )
k =0
Как следует из записи полинома в исходной форме (2), коэффициент при
n |
fk |
|
|
||
xn равен an = ∑ |
|
. |
|||
(k ) |
|||||
k =0 |
Ln |
(xk ) |
|
||
Приведем еще одну форму записи интерполяционного полинома:
Pn (x)= A0 + A1 (x − x0 )+ A2 (x − x0 )(x − x1 )+... + An (x − x0 )(x − x1 )...(x − xn−1 )(3)
21
Требование совпадения значений полинома с заданными значениями функции приводит к системе линейных уравнений с треугольной матрицей для неопределенных коэффициентов{Ai ;i = 0,1,..., n}:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0 = f0 |
|
||
|
|
|
|
|
|
|
|
A0 + A1 |
(x1 − x0 )= f1 |
|
||||||||
|
|
|
(x |
|
|
|
)+ A |
(4) |
||||||||||
A |
+ A |
2 |
− x |
0 |
(x |
2 |
− x |
0 |
)(x |
2 |
− x |
)= f |
2 |
|||||
|
0 |
1 |
|
|
2 |
|
|
|
|
1 |
|
|
||||||
|
|
|
... |
|
|
|
... |
|
... |
|
|
|
... |
|
=... |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
В дальнейшем будет рассмотрено решение систем линейных уравнений приведением к треугольному виду (метод исключения Гаусса).
Решение такой системы уравнений не составляет труда. Интерполяционный полином, записанный в виде (3), называется полино-
мом Ньютона.
Он интересен тем, что каждая частичная сумма его первых m +1слагаемых представляет собой интерполяционный полином m -ой степени, построенный по первым m +1 табличным данным.
n |
fk |
|
|
||
Используя выведенное нами соотношение an = ∑ |
|
(*), решение |
|||
(k ) |
|||||
k =0 |
Ln |
(xk ) |
|
||
треугольной системы уравнений сразу можно записать в явном виде:
n |
fk |
|
|
||
Am = ∑ |
|
, m = 0,1,..., n (5) |
|||
(k ) |
|||||
k =0 |
Ln |
(xk ) |
|
||
В силу единственности решения задачи о построении интерполяционного полинома - записи в форме Лагранжа и Ньютона - это различные формы записи одного полинома.
Интересно сопоставить эти формы записи с точки зрения удобства использования при практическом интерполировании.
Замечание.
Если надо вычислить приближенное значение функции при некоторомx ≠ xi , то это вовсе не означает, что надо привлекать интерполяционный полином, построенный по всем табличным значениям. Это неправильно. Поступают так: строят полином невысокой степени по точкам, ближайшим к точке x и по ним вычисляют f (x).
22
Полином Лагранжа следует применять, если требуется приближать различные функции, заданные табличными значениями в одних и тех же точках.
|
Если в качестве результата нужна непосредственно формула, прибли- |
|||||||||
жающая |
функцию |
|
f (x), |
то, |
конечно, |
предпочтительнее |
||||
P |
(x)= a |
0 |
+ a x + a |
2 |
x2 +... + a |
n |
xn или ИП в форме Ньютона. |
|
||
n |
|
1 |
|
|
|
|
|
|||
Чтобы вычислить коэффициенты полинома (*), нужно решать систему уравнений общего вида (с определителем Вандермонда), а коэффициенты полинома Ньютона вычисляются из простой треугольной системы уравнений или непосредственно вычисляются по формуле (5).
Пример.
Допустим, что вблизи точкиx = x0 мы построили полином третьей степени
(по точкамx0 , x1, x2 , x3 ), а затем выяснилось, что точность, которую он обеспе-
чивал, недостаточна, и надо использовать интерполяцию четвертой степени. Для полинома Ньютона повышение его порядка на единицу сводится к
добавлению одного слагаемого, т.е. в нашем случае к вычислению коэффициента .
В то же время для ИП в исходной форме или ИП в форме Лагранжа нужно повышать порядок решаемой системы линейных уравнений (в данном случае делать его 4-го порядка).
Замечание.
Разумеется, ИП в форме Ньютона можно записать в окрестности любой табличной точки, “назвав” ее узлом x0 , а ближайшие табличные точки (с лю-
бой стороны и в любом порядке) - узлами x1 , x2 и т.д.
Погрешность интерполяции.
Ошибка приближения функции ИП n -ой степени в т. x - это разность
Rn (x)= f (x)− Pn (x).
Для оценки величины погрешности справедлива следующая теорема.
Теорема. Пусть на отрезке [a;b], таком, |
что [x0 ; xn ] [a;b] функция f (x) |
(n +1) раз непрерывно дифференцируема, т.е. |
f Cn+1([a;b]), |
23
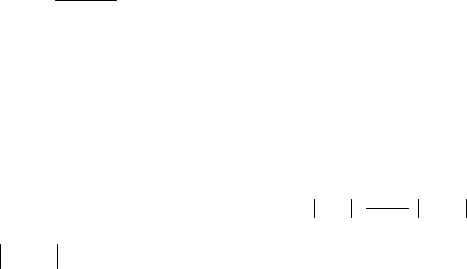
тогда Rn (x) = |
f n+1 (x') |
ωn+1 (x) (6), гдеx′ [a;b]. |
|
(n +1)! |
|||
|
|
Доказательство.
Будем искать погрешность в виде Rn (x) = C(x) ωn+1 (x) , где C(x) - функция,
ограниченная на [a;b]. (При этом гарантируется, что Rn (x) обращается в ноль в точках интерполяции)
Чтобы получить представление о C(x) , рассмотрим вспомогательную
функцию
φ(x) = f (x) − Pn (x) − C(ξ) ωn+1 (x) , где ξ [a;b] - некоторое фиксированное значение.
Очевидно, что на [a;b] функция имеет (n + 2) нуля.
Это узлы интерполяции и точка x = ξ.
По теореме Ролля, x' [a;b]:φ(n+1) (x') = 0.
Продифференцировав (*) (n+1) раз и подставив x = x' , получим
0 = φn+1 (x') = f (n+1) (x') − (n +1)!C(ξ) .
Отсюда C(ξ) = f (n+1) (x') . Ясно, что x′ в теореме Ролля зависит от располо-
(n +1)!
жения нулей функции , т.е. x' = x'(ξ) - некоторая неявная зависимость. Обозна-
чая C(ξ) через C(x) получим (6).
доказано.
Следствие.
Из формулы (6) следует оценка интерполяции Rn (x) ≤ (Mn +n+11)! ωn+1 (x) , где
M n+1 = max[ ] f (n+1) (x) .
x a;b
Конкретная величина погрешности в точке зависит, очевидно, от значения полинома ωn+1 (x) в этой точке. Качественный характер ωn+1 (x) изображен на рис. 3.2.
24

Рис 3.2. Качественный характер
За пределами отрезка интерполяции (т.е. при экстраполяции) ωn+1 (x) бы-
стро растет; экстремальные значения меньше в середине отрезка интерполяции.
Для равноотстоящих узлов (xi = x0 +ih) для x [x0 ; xn ] имеет место
max |
|
ωn+1 (x) |
|
≈ |
ωn+1 (x0 |
+ |
h |
) |
≤ h h (2h) (3h)...(nh)= n!hn+1 |
, где |
|
|
|||||||||
|
|
2 |
||||||||
x |
|
|
|
|
|
|
|
|
|
n
ωn+1 (x) = (x − x0 )(x − x1 )...(x − xn )= ∏(x − xi )
i=0
Поэтому на отрезке интерполяции x [x0 ; xn ]
Rn (x) ≤ (Mn +n+11) hn+1 (8)
Оценка (8) - сильно завышенная оценка ошибки. Для получения точной оценки надо искать экстремумы ωn+1 (x) .
Оценка (7) для погрешности интерполяции не является завышенной. Можно показать, например, что она достигается при интерполировании полиномом n -ой степени полиномом (n +1) степени.
Пример.
Пусть f (x) =  x, [a;b] - отрезок [100;144].
x, [a;b] - отрезок [100;144].
Построить интерполяционный многочлен второго порядка P2 (x) в узлах
x0 =100, |
x1 =121, |
x2 =144. |
25
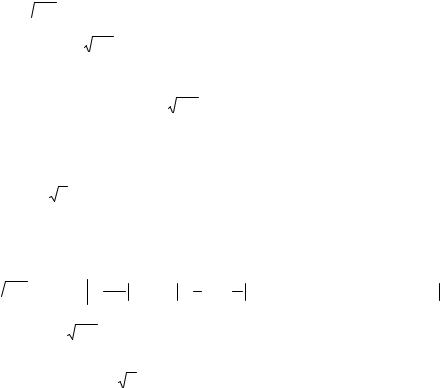
Оценить погрешность интерполяции в т. x =116 и на всем отрезке [a;b].
Решение.
ИП Ньютона P2 (x)= A0 + A1(x − x0 ) + A2 (x − x0 )(x − x1) .
Для коэффициентов Ai :
A0 = f (x0 )
A0 + A1(x1 − x0 ) = f (x1)
A0 + A1(x2 − x0 ) + A2 (x2 − x1) = f (x2 )
В данном случае:
A0 =  100 =10 ;
100 =10 ;
A |
|
= f1 − A0 = |
121 −10 = 1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
− x0 |
|
121−100 |
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
f2 − A0 − A1(x2 − x0 ) |
|
|
|
|
144 −10 |
− |
|
1 |
|
(144 −100) |
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
A |
|
= |
|
= |
|
|
|
|
|
|
|
21 |
|
|
|
|
= − |
; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
(x2 |
− x0 )(x1 − x0 ) |
|
|
|
|
|
|
(144 −100)(121−100) |
|
|
9702 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
1 |
|
− |
3 |
|
|
|
|
|
3 |
− |
5 |
|
|
|
||
|
|
|
|
|
|
|
|
2 ; |
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
||||||||||||
f |
'(x) = |
|
|
|
= |
|
|
|
x |
|
|
|
|
|
|
f |
''= − |
|
x |
|
2 |
|
|
f '''= |
|
x |
2 |
|
|
|
||||||||
|
|
|
|
2 |
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
− 52 |
|
3 |
|
|
−5 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
M3 = |
max |
|
|
f |
′′′ |
= |
|
|
|
100 = |
|
|
10 . |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
x [a;b] |
|
|
|
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

 116 − P2 (116) ≤ M3!3 ω3 (116) = 8310−5 31! (116 −100)(116 −121)(116 −144) =1.4 10−3
116 − P2 (116) ≤ M3!3 ω3 (116) = 8310−5 31! (116 −100)(116 −121)(116 −144) =1.4 10−3
1) |
|
116 − P (116) |
|
≤1.4 10−3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
|
x − P |
(x) |
|
≤ |
M |
3 |
|
hn+1 |
|
= |
3 |
|
1 |
10−5 203 =10−2 . |
||||
|
max |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x [100;144] |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n +1 |
|
|
8 |
3 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Оценка 2) сильно завышена.
Замечания о минимизации ошибки при полиномиальной интерполяции.
Rn (x) = |
f n+1 (x) |
ωn+1 (x') ,где x′ [a;b] . |
|
(n +1)! |
|||
|
|
Ясно, что величина ошибки зависит от расположения узлов Если узлы можно выбирать, то ситуация значительно улучшается. Можно минимизировать ошибку интерполяции.
26
Полиномы Чебышева. Интерполяция по чебышевским узлам.
При больших n ≥10 интерполяция по равноотстоящим узлам практически не используется:
1. может не быть сходимости, (функция Рунге f (x)= |
|
1 |
, f (x) C ∞ [a;b], |
|
+ 25x2 |
||
1 |
|
||
но ошибка интерполяции с ростом n бесконечно возрастает.)
2. даже малые погрешности в табличных данных приводят к большим (неустранимым) ошибкам интерполяции.
При интерполяции по чебышевским узлам этих неприятностей нет.
Рис. 3.3 Функция Рунге
Ошибка интерполяции В таблице.1 приведены результаты приближения интерполяционными по-
линомами различной степени функции Рунге
|
|
|
|
|
|
|
|
|
|
|
Таблица.3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
0,7 ≤ |
|
x |
|
≤1 |
|
|
x |
|
< 0.7 |
Чебышевские |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
узлы |
|
|
|
|
|
|
|
|
||||
4 |
0,44 |
|
|
|
|
0,37 |
0,40 |
||||
|
|
|
|
|
|
|
|
||||
8 |
1,01 |
|
|
|
|
0,24 |
0,17 |
||||
|
|
|
|
|
|
|
|
||||
10 |
1,88 |
|
|
|
|
0,3 |
0,11 |
||||
|
|
|
|
|
|
|
|
||||
20 |
40,0 |
|
|
|
|
0,12 |
0,01 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
27
Функция Рунге - “нехорошая” для интерполирования функция.
Пример.
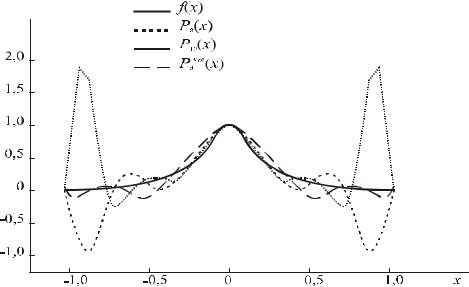
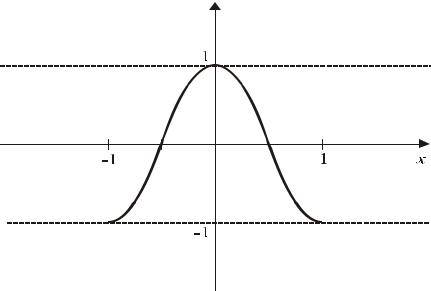
f (x) = cos(πx), x [−1; 1] - “хорошая” для интерполяции функция (Рис. 3.4).
Рис. 3.4 График функции f (x)= cos(πx)
Результаты приближения приведены в таблице.2
|
|
|
|
|
Таблица.3.2 |
|
|
|
|
|
|
n |
Ошибка интерполяции |
|
|
|
|
|
|
|
|
|
|
|
Точные |
неточ. |
Чеб.узлы, |
Чеб. узлы, |
|
|
вход.дан. |
вход. дан. |
точ. вх.дан. |
неточ. вх.дан |
|
|
|
≤ 0.01 |
|
|
≤ 0.01 |
|
|
|
|
|
|
4 |
0.09 |
0.10 |
0.060 |
0.061 |
|
|
|
|
|
|
|
8 |
0.0003 |
0.007 |
0.0001 |
0.0009 |
|
|
|
|
|
|
|
10 |
1.3 10-5 |
0.012 |
1.5 |
10-6 |
0.0095 |
|
|
|
|
|
|
20 |
3 10-9 |
15.3 |
2.5 |
10-11 |
0.011 |
|
|
|
|
|
|
28
