Вопросы к экзамену по линейной алгебре

МП-1А

1. Поле. Примеры полей. Поле остатков от деления на p.

2. Линейное пространство над полем. Его простейшие свойства.

3. Линейно зависимые и независимые системы векторов. Их свойства.

4. Полные системы векторов. Их свойства.

5. Базис линейного пространства. Единственность разложения по базису.

6. Лемма Штейница и следствия из нее. Размерность линейного пространства.

7. Подпространство линейного пространства. Сумма и пересечение подпространств.

8. Линейная оболочка совокупности векторов.

9. Размерность суммы подпространств.

10. Подстановки. Количество инверсий. Транспозиции. Обратная подстановка.

11. Операции над матрицами. Ассоциативность произведения матриц.

12. Определитель. Неизменность определителя при транспонировании матрицы. Линейность определителя.

13. Перестановка строк (столбцов) определителя. Определитель с двумя одинаковыми строками (столбцами).

14. Определитель блочной матрицы.

15. Разложение определителя по строке (столбцу).

16. Определитель произведения матриц.

17. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.

18. Ранг матрицы. Теорема о базисном миноре.

19. Обратная матрица: единственность, условие существования, методы вычисления.

20. Правило Крамера.

21. Свойства решений однородной системы линейных уравнений. Связь решений однородной системы с решениями неоднородной.

22. Фундаментальная система решений однородной системы.

23. Переход к другому базису в линейном пространстве.

24. Линейные операторы. Матрица линейного оператора. Связь координат образа и прообраза.

25. Изменение матрицы линейного оператора при изменении базиса.

26. Собственные векторы и собственные значения линейного оператора. Характеристическое уравнение.

27. Свойство собственных векторов линейного оператора.

28. Условие приведения матрицы к диагональному виду.

29. Евклидовы и унитарные пространства. Неравенство Шварца. Геометрия евклидовых пространств.

30. Ортогональный и ортонормированный базис. Процесс ортогонализации Грама-Шмидта.

31. Ортогональные матрицы.

32. Симметрические (самосопряженные) операторы. Свойства их матриц.

33. Свойства собственных значений и собственных векторов симметрического оператора. Существование для симметрического оператора ортонормированного базиса из собственных векторов.

34. Линейные, билинейные и квадратичные формы.

35. Матрица квадратичной формы. Изменение матрицы при изменении базиса.

36. Приведение действительной квадратичной формы к нормальному виду.

37. Положительно определенные и отрицательно определенные квадратичные формы. Критерий Сильвестра.

БИЛЕТ 1. Поле. Примеры полей. Поле остатков от деления на p.

Определение поля:

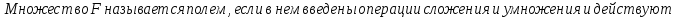
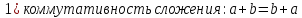
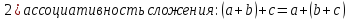
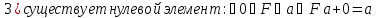
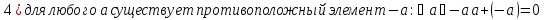
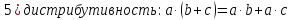
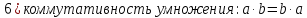
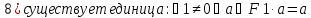
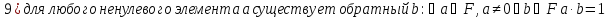
Элементы поля принято называть скалярами.

Примеры полей:

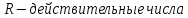
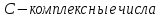
Множество 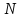натуральных чисел полем не является, так как в нем не выполняется 9 аксиома.

Свойства поля:

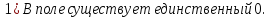
Доказательство:

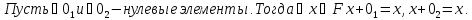
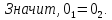
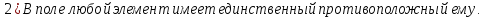
Доказательство:

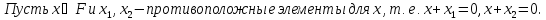
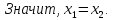
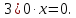
Доказательство:

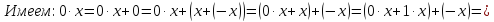
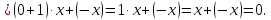
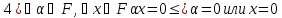
Доказательство:

.

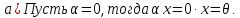
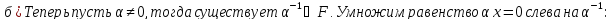
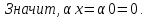
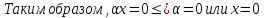Сравнение по модулю p:

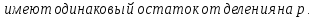
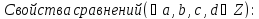
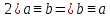
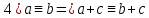
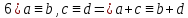
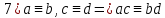
Множество остатков от деления на p:

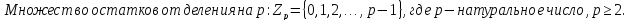
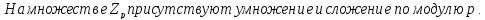
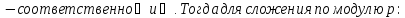
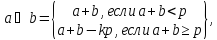
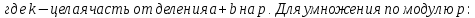
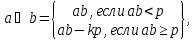
Поле остатков от деления на p:

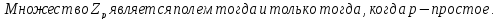
Доказательство:

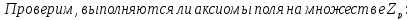
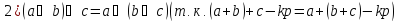
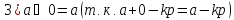
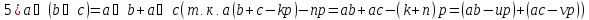
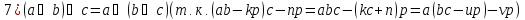
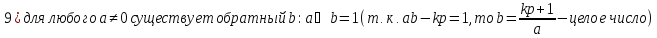
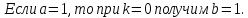
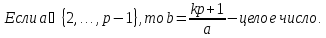
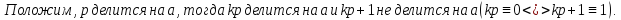
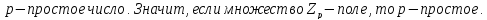
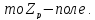
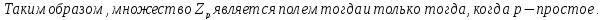
БИЛЕТ 2. Линейное пространство над полем. Его простейшие свойства.

Определение линейного пространства:

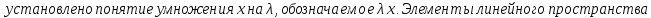
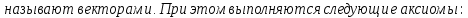
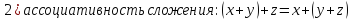
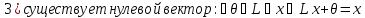
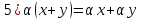
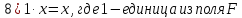
Простейшие свойства линейного пространства:

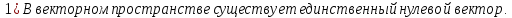
Доказательство:

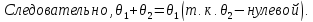
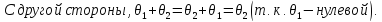
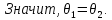
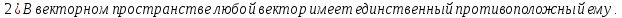
Доказательство:

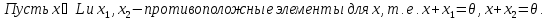
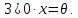
Доказательство:

Доказательство:

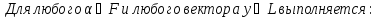
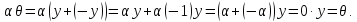
Доказательство:

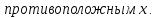
Доказательство:

.

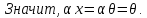
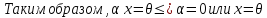БИЛЕТ 3. Линейно зависимые и независимые системы векторов. Их свойства.

Определение линейной комбинации векторов:

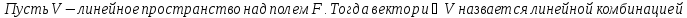
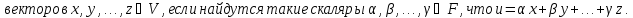
Определение линейно зависимой системы векторов:

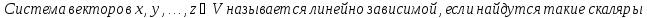
Определение линейно независимой системы векторов:

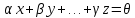
Необходимое и достаточное условие линейной зависимости векторов:

Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.

Доказательство:

1) Необходимость:

Пусть элементы

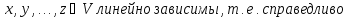
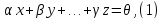
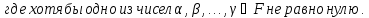
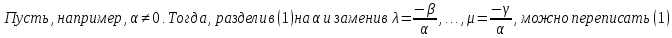
2) Достаточность:

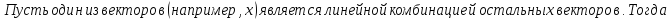
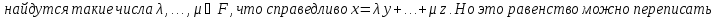
Теорема доказана.

Свойства (следствия):

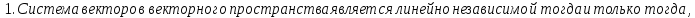
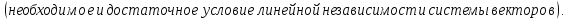
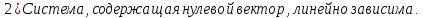
Доказательство:

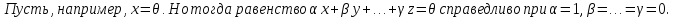
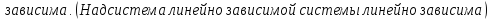
Доказательство:

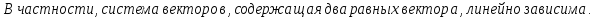
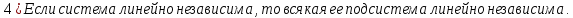
Доказательство:

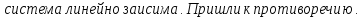
БИЛЕТ 4. Полные системы векторов. Их свойства.

Определение полной системы векторов:

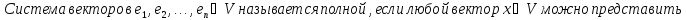
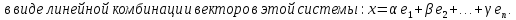
Свойства:

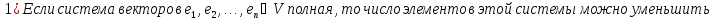
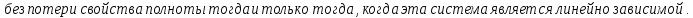
Доказательство:

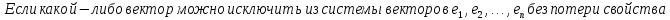
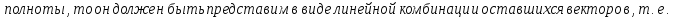
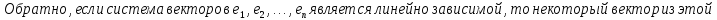
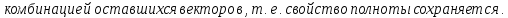
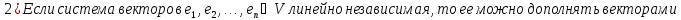
Доказательство:

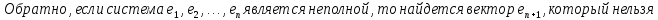
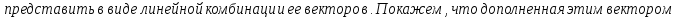
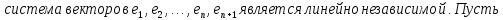
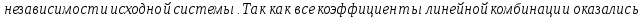
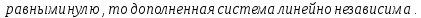
БИЛЕТ 5. Базис линейного пространства. Единственность разложения по базису.

Определение базиса линейного пространства:

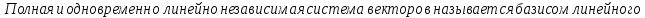
Единственность разложения по базису:

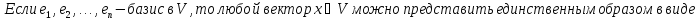
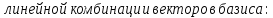
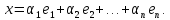
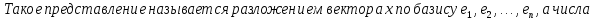
Доказательство:

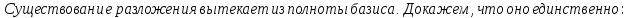
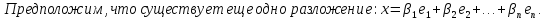
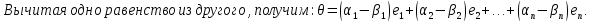
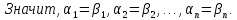
БИЛЕТ 6. Лемма Штейница и следствия из нее. Размерность линейного пространства.

Лемма Штейница о замене:

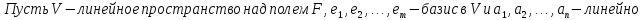
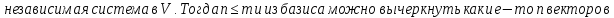
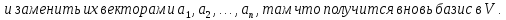
Доказательство:

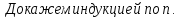
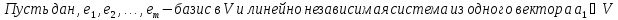
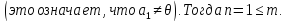
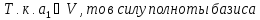
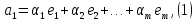
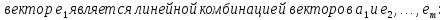
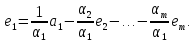
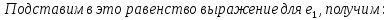
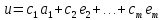
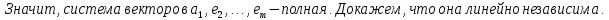
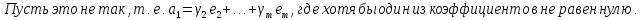
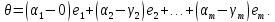
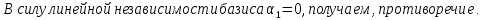
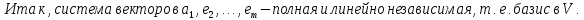
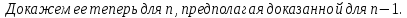
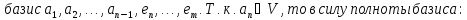
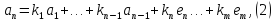
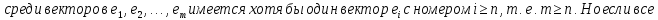
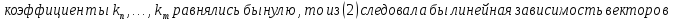
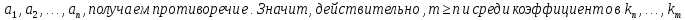
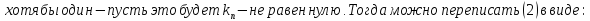
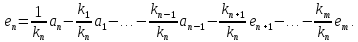
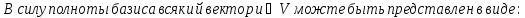
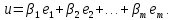
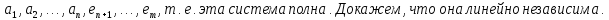
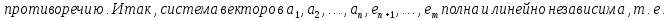
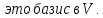
Следствия:

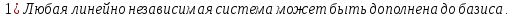
Доказательство:

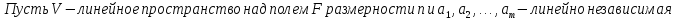
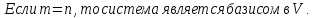
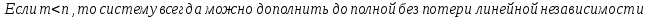
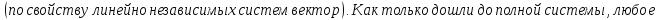
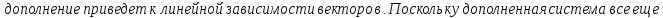
Доказательство:

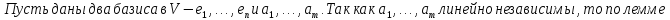
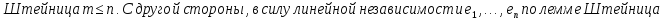
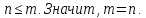
Размерность линейного пространства:

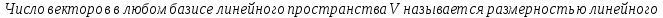
БИЛЕТ 7. Подпространство линейного пространства. Сумма и пересечение подпространств.

Определение подпространства линейного пространства:

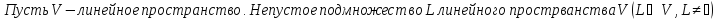
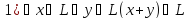
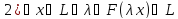
Замечание:

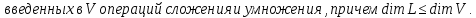
Доказательство:

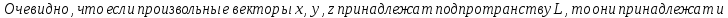
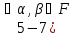
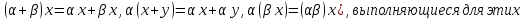
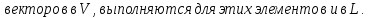
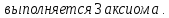
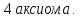
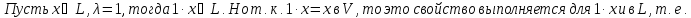
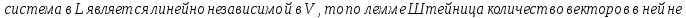
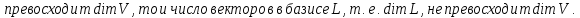
Определения суммы и пересечения подпространств:

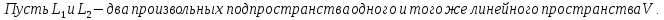
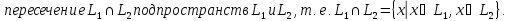
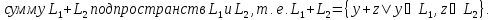
Свойства суммы и пересечения подпространств:

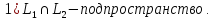
Доказательство:

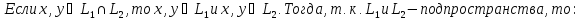
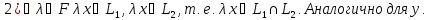
Доказательство:

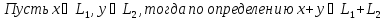
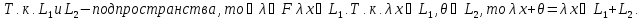
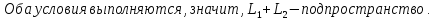
БИЛЕТ 8. Линейная оболочка совокупности векторов.

Определение линейной оболочки:

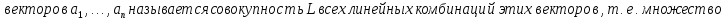
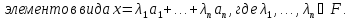
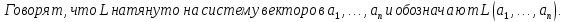
Свойства:

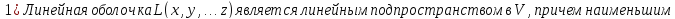
Доказательство:

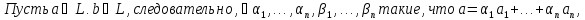
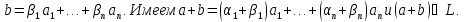
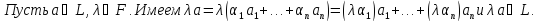
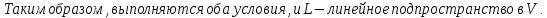
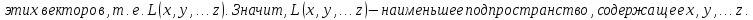
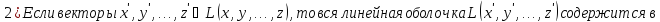
Доказательство:

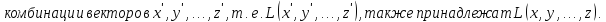
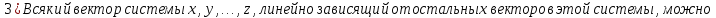
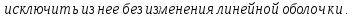
Доказательство:

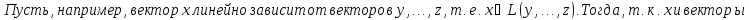
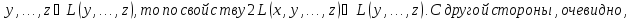
БИЛЕТ 9. Размерность суммы подпространств.

Теорема:

Доказательство:

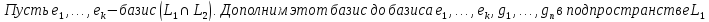
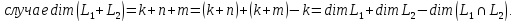
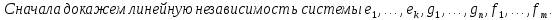
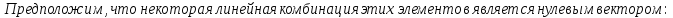
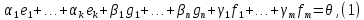
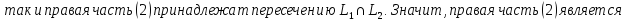
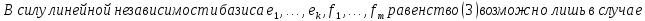
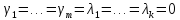
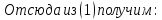
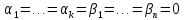
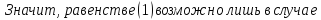
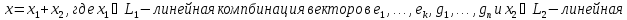
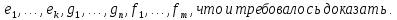
БИЛЕТ 10. Подстановки. Количество инверсий. Транспозиции. Обратная подстановка.

Определение подстановки:

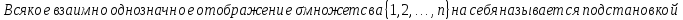
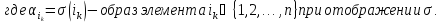
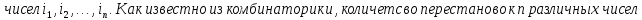
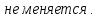
Основные понятия:

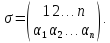
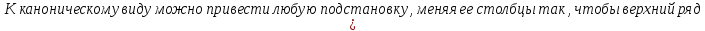
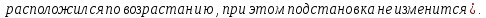
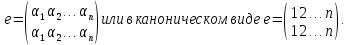
Определение инверсий, количества инверсий и транспозиции:

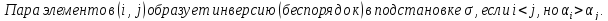
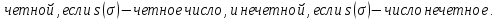
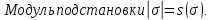
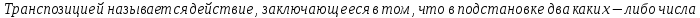
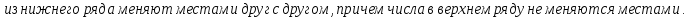
Свойства транспозиции:

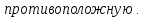
Доказательство:

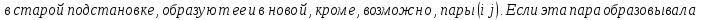
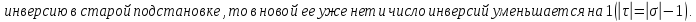
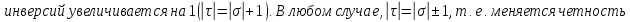
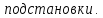
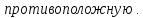
Доказательство:

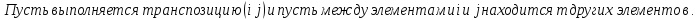
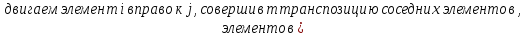
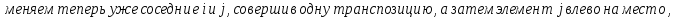
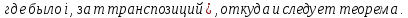
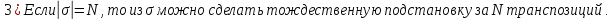
Доказательство: