Отчет к упражнению 1

Создать M-функцию, которая строит в одной системе координат график последовательности членов ряда и график последовательности частичных сумм ряда. При построении этой пары графиков использовать разные цвета и маркеры. В качестве входных параметров M-функции использовать формулу общего члена последовательности и число рассматриваемых членов. В качестве выходных параметров вывести значения . Применить созданную М-функцию для исследования следующих рядов:

1) ; 2) ; 3) .

Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.

М-функция:

function [s1,s2,s3,s4,s5]=sumplot(an,n0)

n=1:1:n0;

y=subs(an,n);

grid on;hold on;axis equal;

plot(n,y);

s=subs(an,1);

cs=s;

for n=2:1:n0;

cs=cs+subs(an,n);

s=[s;cs];

end

n=1:1:n0;

plot(n,s(n),'--r');

s1=s(n0-4);

s2=s(n0-3);

s3=s(n0-2);

s4=s(n0-1);

s5=s(n0);

end

Проверка на примерах:

1)

[s1,s2,s3,s4,s5]=sumplot('1/n',50)

s1 =

4.4167

s2 =

4.4380

s3 =

4.4588

s4 =

4.4792

s5 =

4.4992

Вывод: ряд расходится.

2) ;

[s1,s2,s3,s4,s5]=sumplot('1/sqrt(n)',50)

s1 =

12.1779

s2 =

12.3238

s3 =

12.4681

s4 =

12.6110

s5 =

12.7524

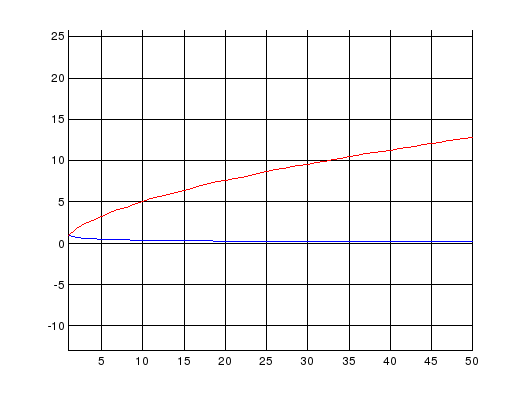
Вывод: ряд расходится.

3) .

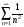[s1,s2,s3,s4,s5]=sumplot('1/n^2',100)

s1 =

1.6346

s2 =

1.6347

s3 =

1.6348

s4 =

1.6349

s5 =

1.6350

Вывод: ряд сходится.

n=1:1:10000000;

s=sum(1./n.^2)

s =

1.6449

Отчет к упражнению 2

Установить, расходимость каких из следующих рядов можно доказать, используя необходимый признак сходимости (по Вашему желанию: «вручную» или используя MATLAB):

а)

sumplot('((n+1)^(1/3)-1)/n',50)

Вывод: необходимое условие выполняется, но ряд расходится.

б)

sumplot('((n+3)/(n+1))^(2*n-1)',10)

Вывод: необходимое условие не выполняется, поэтому ряд расходится.

Отчет к упражнению 3

Приведите два примера расходящихся числовых рядов (отличные от рассмотренных в упр. 2), общий член которых стремится к нулю. Используя M-функцию из упр. 1, проиллюстрируйте примеры графически.

sumplot('2/n',50);

sumplot('2/n^(1/5)',50)

Отчет к упражнению 4

а) Пусть ряд сходится, расходится. Что можно сказать о сходимости ряда ? Проиллюстрируйте Ваше предположение на примере, используя М-файл из упр. 1.

Если есть сходящийся и расходящийся ряды, то их сумма расходится (иначе получили бы: сх + расх = сх, расх = сх – сх = сх, противоречие):

sumplot('1/n',50);

sumplot('1/n^2',50);

sumplot('1/n+1/n^2',50);

б) Пусть ряды и расходятся. Что можно сказать о сходимости ряда ? Проиллюстрируйте Ваши предположения на примерах, используя М-файл из упр. 1.

Про сумму расходящихся рядов ничего сказать нельзя (поскольку, если расх+расх=сх, то расх=сх-расх=расх, противоречия нет, поэтому может быть как расх+расх=расх, так и расх+расх=сх):

РАСХ+РАСХ=РАСХ

sumplot('1/n+1/n^(1/4)',50);

РАСХ+РАСХ=СХ

sumplot('(-1/n)',100);

sumplot('1/n+(-1/n)',100);

Отчет к упражнению 5

Опираясь на признаки сходимости, доказать:

а) ряд расходится

б) ряд сходится

в) ряд расходится

г) ряд 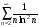сходится

Отчет к упражнению 6

Пусть к ряду 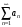применимо утверждение об оценке ряда. Создайте M-функцию, которая оценивает число членов, достаточное для вычисления суммы ряда с заданной точностью , и вычисляет сумму ряда с заданной точностью. В качестве входных параметров M-функции используйте формулу общего члена последовательности и точность . Применить созданную М-функцию для вычисления с точностью до 0,001 суммы ряда:

Указание. Для ряда а) имеем: - при увеличении монотонно уменьшается от до . Для ряда б): - убывает от до нуля. Наша М-функция может содержать два цикла. В первом цикле, начиная с , вычисляем и до тех пор пока выполняется неравенство 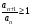. Во втором цикле продолжаем вычислять и , а также . Второй цикл заканчивается при выполнении условия . Выходными параметрами М-функции должны быть и .

function [n,s]=sumvalue(an,eps)

n=1;

q=an(2)/an(1);

s=an(1);

while(q>=1)

n=n+1;

s=s+an(n);

q=an(n+1)/an(n);

end

r=an(n+1)/(1-q);

while(r>eps)

n=n+1;

q=an(n+1)/an(n);

s=s+an(n);

r=an(n+1)/(1-q);

end

end

а)

[n,s]=sumvalue(@(n)n/2^n,0.001)

n =

14

s =

1.9990

б)

[n,s]=sumvalue(@(n)1/factorial(n),0.001)

n =

6

s =

1.7181

Отчет к упражнению 7

Создать M-функцию, которая оценивает число членов знакочередующихся рядов, достаточное для вычисления суммы ряда с заданной точностью , и вычисляет сумму ряда с заданной точностью. В качестве входных параметров M-функции использовать формулу общего члена последовательности и точность .

function [n,s]=sumsign(an,eps)

n=1;

r=abs(an(n+1));

s=an(1);

while(r>eps)

n=n+1;

s=s+an(n);

r=abs(an(n+1));

end

end

Для следующих рядов доказать сходимость и применить созданную М-функцию для вычисления с точностью до 0,001 суммы ряда:

а)

[n,s]=sumsign(@(n)((-1)^(n-1))*1/n,0.001)

n =

999

s =

0.6936

б)

[n,s]=sumsign(@(n)((-1)^(n-1))*1/n^2,0.001)

n =

31

s =

0.8230

Отчет к упражнению 1C

Для рядов 1) ; 2) ; 3) выполнить следующие задания:

а) используя M-функцию, созданную в процессе выполнения упр. 1, построить в одной системе координат график последовательности членов ряда и график последовательности частичных сумм ряда. Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.

1)

sumplot('0.3^n',10);

Ряд сходится:

n=1:1:1000;

s=sum(0.3.^n)

s =

0.4286

2)

sumplot('1.5^n',10);

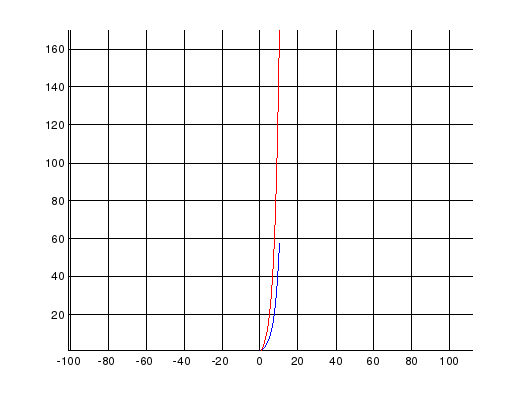
Ряд расходится.

3)

sumplot('1/(n^2+2*n)',50);

Ряд сходится:

n=1:1:1000000;

s=sum(1./(n.^2+2*n))

s =

0.7500

б) Доказать, опираясь на определение, выдвинутую гипотезу о сходимости (расходимости) ряда, и в случае сходимости ряда, найти точное значение суммы.

1)

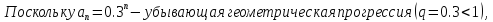
2)

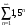
3)

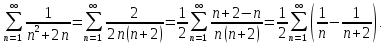
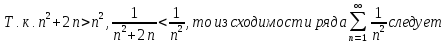
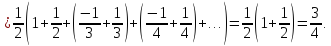
Отчет к упражнению 2C

Опираясь на признаки сходимости, доказать:

а) ряд сходится

б) ряд сходится

в) ряд сходится

г) 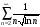расходится