
- •Технология изготовления оптического волокна
- •Принципы функционирования световых волноводов
- •Дисперсия световых сигналов
- •Распространение световой волны в планарном волноводе
- •Te моды
- •Реальные конструкции прямоугольных световых волноводов
- •Te моды
- •Волоконные световые волноводы
- •Волновые уравнения
- •Ступенчатый профиль показателя преломления
- •Граничные условия
- •Характеристики мод
- •Граничные частоты
- •Затухание и дисперсия
- •Литература
Волоконные световые волноводы
Оптические волокна характеризуются своей структурой и характером распространения света вдоль их оптической оси. В основном, оптические волокна классифицируются двумя типами. Первый тип – одномодовые волокна, второй тип – многомодовые волокна. В этих определениях явно подчеркивается, что волокна могут поддерживать распространение света либо одной выделенной моды, либо многих мод одновременно. Основное различие между ними состоит в поперечном размере сердцевины. При этом и одномодовые и многомодовые волокна изготовливаются из одного материала в одном и том же процессе (рис.17).
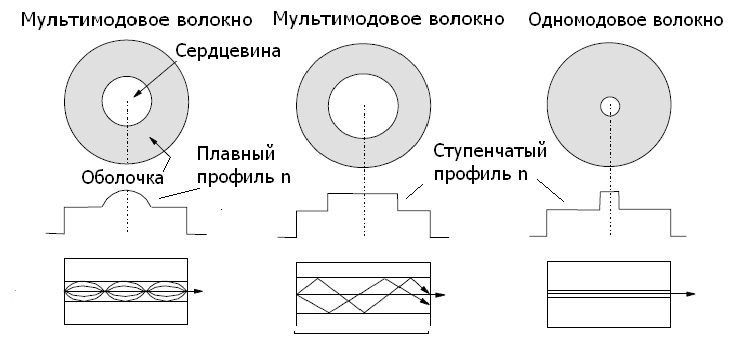
рис.17. Различные типы оптических волокон.
Волновые уравнения
Оптоволокно обладает цилиндрической симметрией, поэтому любая точка внутри волокна определяется тремя координатами: r – радиусом, относительно выделенной нулевой точки на оптической оси, углом φ между оптической осью и радиусом-вектором r, и координатой z, являющейся проекцией рассматриваемой точки на оптическую ось.
Волновое уравнение (без учета гармонической составляющей с круговой частотой ω) для рассматриваемых векторов светового поля, например, электрического вектора E имеет вид:
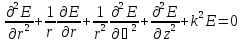 , (63)
, (63)
где k2=k02n2, k0=2π/λ0 – волновое число в вакууме, λ0 – длина световой волны в вакууме.
Рассмотрим световые волны, распространяющиеся вдоль оптической оси. В этом случае они должны иметь следующее функциональное представление:
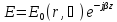 , (64)
, (64)
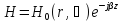 ,
(65)
,
(65)
где параметр β – константа распространения, определяемая из граничных условий световых полей на границе сердцевина волокна – оболочка. Обращаясь к системе уравнений Максвелла, можно записать следующие соотношения для компонент электрического и магнитного векторов светового поля в цилиндрических координатах:
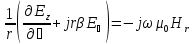 (66)
(66)
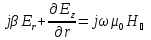 (67)
(67)
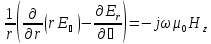 (68)
(68)
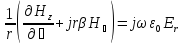 (69)
(69)
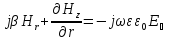 (70)
(70)
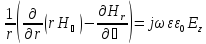 . (71)
. (71)
Преобразовывая эти уравнения, можно выразить поперечные компоненты поля Er, Eφ, Hr и Hφ через продольные компоненты Ez и Hz:
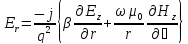 (72)
(72)
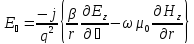 (73)
(73)
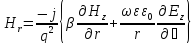 (74)
(74)
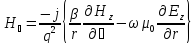 , (75)
, (75)
где q2=ω2μ02(ε ε0)2-β2=k2-β2.
Подставляя (74) и (75) в (71), получаем:
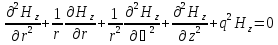 (76)
(76)
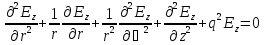 (77)
(77)
Заметим, что (76) и правые части (72)-(75) содержат только Ez или Hz компоненты поля. Это подразумевает, что продольные компоненты E и H несвязанны между собой и могут выбираться произвольно, при условии, что (76)-(77) и (72)-(74) удовлетворяются одновременно. Если граничные условия не ведут к связыванию между компонентами поля, то или Ez=0, или Hz=0. Когда Ez=0, то такие моды называются поперечными электрическими, или TE-модами, когда Hz=0, то они называются поперечными магнитными, или TM-модами. В принципе, могут существовать и гибридные моды, если граничные условия это позволяют. Гибридные моды существуют тогда, когда Hz и Ez имеют ненулевые значения. В зависимости от того, какая компонента поля превалирует в этом случае, имеются поперечные TEM или THM гибридные моды распространения света в оптоволокне.
Ступенчатый профиль показателя преломления
Стандартная процедура разделения переменных состоит в представлении возможных решений, например, для Ez компонент, в виде:
 , (78)
, (78)
где A – постоянный множитель.
Так же как и в случае прямоугольных волноводов предположим, что зависимость от координаты z имеет вид
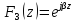 , (79)
, (79)
где β – постоянная распространения световой волны вдоль направления оптической оси.
Также, вследствие симметрии конструкции волновода, каждая компонента поля не должна меняться при изменении угла φ на 2π, поэтому
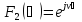 . (80)
. (80)
В уравнении (79), постоянная величина ν может принимать только целочисленные значения: ν=0, ±1, ±2, …, т.к. поле должно быть периодическим при изменении φ с периодом 2π.
Подставляя (79) и (80) в (77), получаем:
 . (81)
. (81)
Это хорошо известное выражение, решениями которого являются функции Бесселя. Точно такое же уравнение имеет место и для Hz. Рассмотрим однородный сердечник волокна с показателем преломления равным n1 с радиусом a, окруженным оболочкой с радиусом, существенно превышающим размер сердечника с показателем преломления n2. В этом случае характер распространения световых волн не зависит от радиуса оболочки по причине быстрого затухания световых волн в этой среде. Кроме того, реальные световые волокна имеют радиус оболочки значительно больший, чем радиус сердцевины.
Вначале надо определить, какие из функций Бесселя являются подходящими в этом случае. Если q – действительное число, то решениями уравнения (81) являются либо
 - функция Бесселя первого рода, или
- функция Бесселя первого рода, или
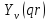 - функция Бесселя второго рода.
- функция Бесселя второго рода.
Число ν, которое может принимать только целочисленные значения, называется порядком функции, а qr – аргументом функции. Графики функций Jν(qr) и Yν(qr) для нескольких первых значений ν приведены на рис.18, 19.
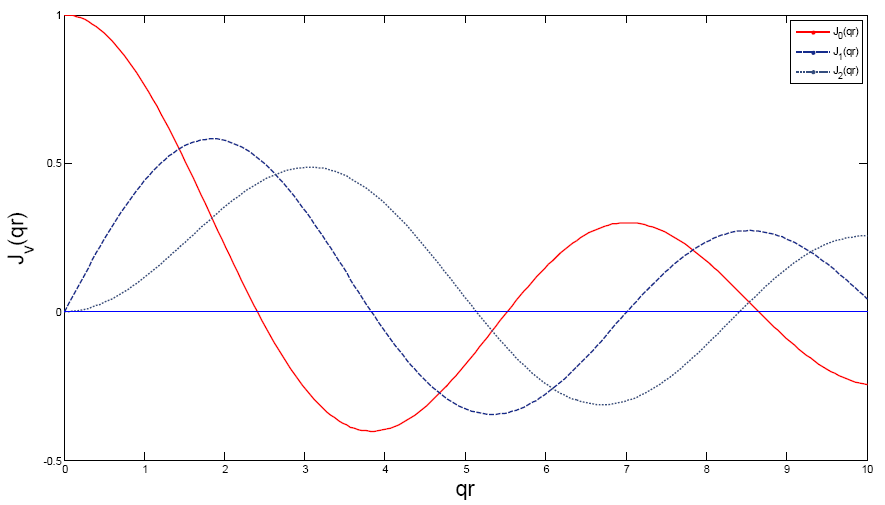
рис.18. График функций Бесселя первого рода для действительного значения q при значениях ν=0, 1, 2.
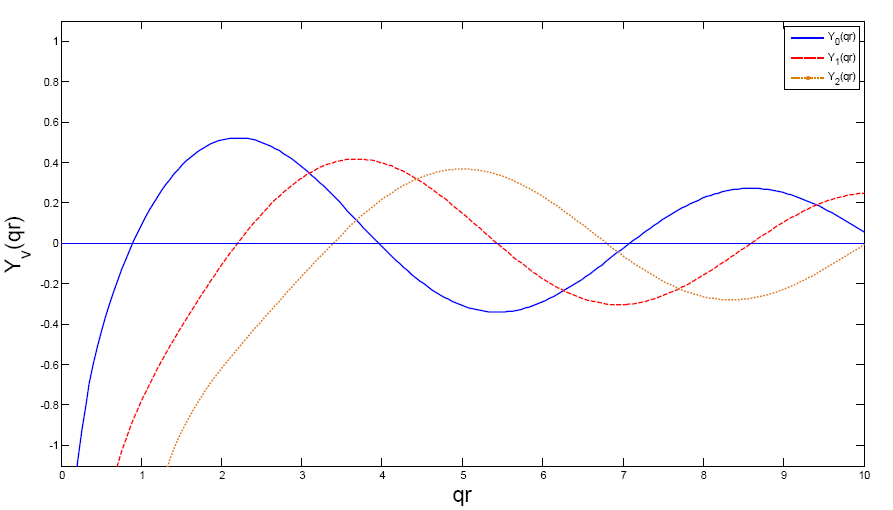
рис.19. График функций Бесселя второго рода для действительного значения q при значениях ν=0, 1, 2.
Можно видеть, что за исключением J0 все остальные функции Бесселя первого рода стремятся к нулю при стремлении к нулю аргумента функций. При этом только J0 стремиться к единичному значению. С другой стороны, функции Бесселя Yν расходятся при стремлении аргумента к нулю, поэтому они должны быть исключены из решения задачи. Функции первого рода монотонно уменьшаются при стремлении аргумента к бесконечности, поэтому правильная комбинация этих функций является решением для распределения светового поля внутри сердечника оптоволокна.
Решениями уравнения Бесселя, которые появляются при решении внешней краевой задачи (оболочка оптоволокна)
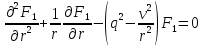 , (82)
, (82)
являются модифицированные функции Бесселя Iν(qr) и Kν(qr) первого и второго рода. Графики этих функций показаны на рис.20, 21.
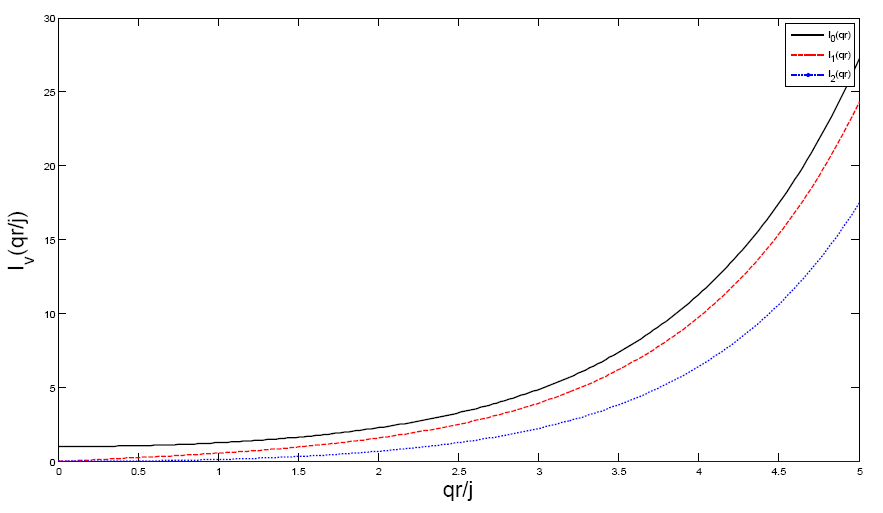
рис.20. Модифицированные функции Бесселя первого рода Iν(qr) для действительного значения q при значениях ν=0, 1, 2.
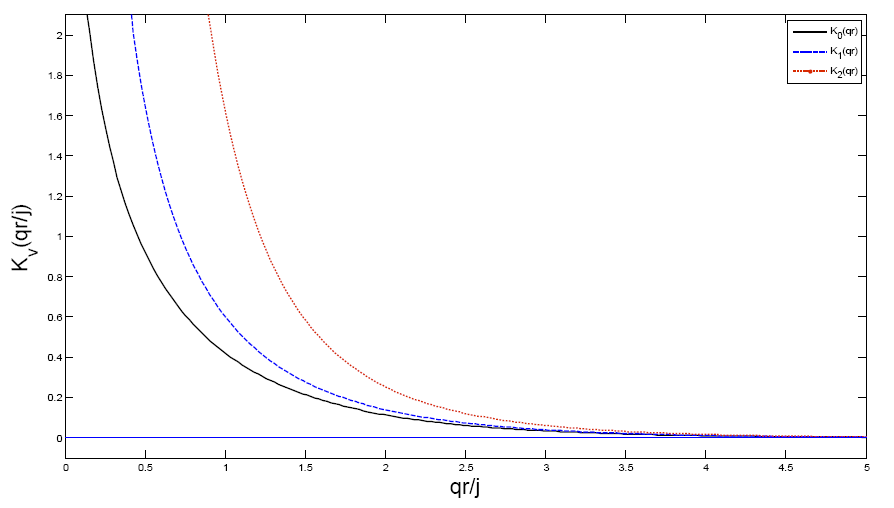
рис.21. Модифицированные функции Бесселя второго рода Kν(qr) для действительного значения q при значениях ν=0, 1, 2.
Из рассмотрения графиков 20 и 21 следует, что Iν(qr) неограниченно возрастает при стремлении аргумента к бесконечности. С другой стороны, функция Kν(qr) быстро стремится к нулю при увеличении аргумента. Т.к. мы ищем ограниченное решение внешней краевой задачи для оболочки, то единственными подходящими функциями в этом случае являются модифицированные функции Бесселя второго рода Kν(qr).
Т.о., для r<a решениями задачи распространения света по оптоволокну являются функции Бесселя первого рода Jν(ur) порядка ν. При этом u2=k12-β2, где k1=2πn1/λ, λ – длина световой волны в вакууме. Выражения для Ez и Hz внутри сердцевины волновода (r<a) имеет вид:
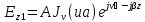 (83)
(83)
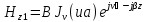 . (84)
. (84)
Вне сердцевины, т.е. в области оболочки решениями будут модифицированные функции Бесселя второго рода, Kν(wa), где w2=β2-k22, k2=2πn2/λ:
 (85)
(85)
 , (86)
, (86)
где A, B, C, D – произвольные постоянные, определяющиеся из граничных условий.
Для световых мод, распространяющихся по оптоволокну, константы распространения мод удовлетворяют условию β2<β<β1 вне и внутри сердцевины волокна. Если n2k≤β≤n1k, то распространение светового поля внутри сердцевины имеет осциллирующий характер и энергия поля быстро уменьшается по мере проникновения в оболочку волокна. В этом случае световая энергия поля сосредоточена в основном в сердцевине и распространяется без потерь вдоль оптоволокна.
