
Лабораторная №9
.docxЛабораторная работа № 9. «Числовые ряды»
Числовой ряд. Частичные суммы ряда. Сходящиеся и расходящиеся ряды. Сумма ряда. Необходимый признак сходимости. Оценка остатка ряда.
Пусть задана бесконечная последовательность
чисел
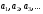 Рассмотрим выражение
Рассмотрим выражение
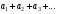 ,
представляющее собой «сумму бесконечного
множества слагаемых». Оно называется
числовым рядом, а
сами числа
,
представляющее собой «сумму бесконечного
множества слагаемых». Оно называется
числовым рядом, а
сами числа
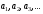 – членами ряда.
– членами ряда.
Член ряда
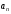 с произвольным номером
с произвольным номером
 называется общим членом.
называется общим членом.
Числа
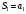 ,
,
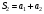 ,
,
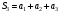 и т.д. называются частичными
суммами ряда. Обобщая:
и т.д. называются частичными
суммами ряда. Обобщая:
 -я
частичная сумма
-я
частичная сумма
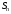 есть сумма первых
есть сумма первых
 членов ряда:
членов ряда:
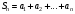 .
.
Если последовательность
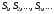 частичных сумм ряда имеет конечный
предел, т.е. существует число
частичных сумм ряда имеет конечный
предел, т.е. существует число
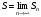 ,
то ряд называется сходящимся, а число
,
то ряд называется сходящимся, а число
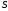 называется суммой ряда. В этом случае
также говорят, что ряд
сходится к сумме
называется суммой ряда. В этом случае
также говорят, что ряд
сходится к сумме
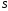 и пишут
и пишут
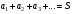 .
.
Если же
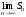 равен бесконечности или не существует,
то говорят, что ряд расходится
или, что он не имеет суммы.
равен бесконечности или не существует,
то говорят, что ряд расходится
или, что он не имеет суммы.
Необходимый признак сходимости.
Если ряд сходится, то его
 -й
член стремится к нулю при
-й
член стремится к нулю при
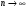 .
.
С помощью этого признака можно доказывать лишь расходимость ряда.
Упражнение 1. Используя MATLAB и необходимый признак сходимости определить расходящийся ряд, не требующий дополнительного исследования:
1)
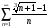 ; 2)
; 2)
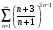 ; 3)
; 3)
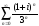 (использовать тригонометрическую форму
представления комплексного числа).
(использовать тригонометрическую форму
представления комплексного числа).
Упражнение 2 (повтор
из лаб. работы первого курса).
Создать M-функцию,
которая строит в одной системе координат
график последовательности членов ряда
и график последовательности частичных
сумм ряда. При построении этой пары
графиков использовать разные цвета и
маркеры. В качестве входных параметров
M-функции использовать
формулу
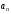 общего члена последовательности и число
общего члена последовательности и число
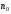 рассматриваемых членов. В качестве
выходных параметров вывести значения
рассматриваемых членов. В качестве
выходных параметров вывести значения
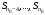 .
Применить созданную М-функцию для
исследования следующих рядов:
.
Применить созданную М-функцию для
исследования следующих рядов:
1)
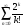 ; 2)
; 2)
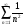 ; 3)
; 3)
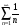 ; 4)
; 4)
 ; 5)
; 5)
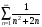 ; 6)
; 6)
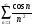 .
.
Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.
Сумму ряда S можно найти с использованием средств Matlab.
В
MATLAB сумма от
 до
бесконечности может быть вычислена
только аналитически; с этой целью
необходимо определить переменную
суммирования (в нашем случае
до
бесконечности может быть вычислена
только аналитически; с этой целью
необходимо определить переменную
суммирования (в нашем случае
 )
с помощью syms;
функция суммирования числовых рядов в
MATLAB имеет вид:
)
с помощью syms;
функция суммирования числовых рядов в
MATLAB имеет вид:
symsum(an, n, n1, n2)
здесь an – член числового ряда, n – переменная суммирования, n1 – начальное значение переменной суммирования, n2 – конечное значение переменной суммирования.
При нахождении суммы ряда в качестве n2 выступает бесконечность; в MATLAB для ее обозначения используется зарезервированный символ inf.
Пример
1.
а) Найти сумму ряда
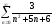 и сравнить с полученным результатом в
упражнении 2;
и сравнить с полученным результатом в
упражнении 2;
б) вычислить частичные суммы при
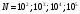 и внести их в таблицу;
и внести их в таблицу;
в) при каждом из указанных
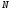 вычислить абсолютную погрешность;
вычислить абсолютную погрешность;
г) при каждом из указанных
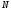 вычислить относительную погрешность
и оценить
вычислить относительную погрешность
и оценить
количество верных цифр и значение суммы.
Решение. а) >> syms n; S_inf=symsum(3/(n^2+5*n+6),n,0,inf)
S_inf = 3/2
б) >> syms N; S=symsum(3/(n^2+5*n+6),n,0,N)
S = -3/(N+3)+3/2
% Сформируем вектор N={102, 103, 104, 105}.
>> N=[10^2, 10^3, 10^4, 10^5] N = 100 1000 10000 100000
% Вычислим значения частичных сумм Si = S(Ni) ряда при соответствующих значениях Ni.
>> S=-3.0./(N+3)+3/2 S = 1.4709 1.497 1.4997 1.5
% Создадим таблицу:
|
i |
Ni |
S(Ni) |
|
1 |
100 |
1.4709 |
|
2 |
1000 |
1.497 |
|
3 |
10000 |
1.4997 |
|
4 |
100000 |
1.5 |
в)
%
Для каждой величины S(Ni)
вычислим абсолютную погрешность
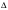 используя встроенную функцию abs:
используя встроенную функцию abs:
>> D=abs(S-3/2)
D = 0.0291 0.0030 0.0003 0.0000
% запишем в другом формате:
>> format long >> D
|
D |
|||
|
0.02912621359223 |
0.00299102691924 |
0.00029991002699 |
0.00002999910003 |
Для отображения погрешности обычно пользуются следующим форматом:
>> format short e >> D
На экране мы увидим:
|
D |
|||
|
2.9126e-002 |
2.9910e-003 |
2.9991e-004 |
2.9999e-005 |
г) %
Для каждой величины S(Ni)
вычислим относительную погрешность
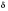 и определим количество верных цифр.
и определим количество верных цифр.
>> d=D./1.5
d =
1.9417e-002 1.9940e-003 1.9994e-004 1.9999e-005
д) Связь относительной погрешности с количеством верных знаков числа
Пусть положительное число
 представлено в виде конечной или
бесконечной десятичной дроби
представлено в виде конечной или
бесконечной десятичной дроби
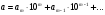 ,
где
,
где
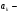 цифра числа
цифра числа
 в
в
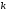 -м
разряде,
-м
разряде,
 – старший десятичный разряд числа.
– старший десятичный разряд числа.
Если положительное
приближенное число
 имеет относительную погрешность
имеет относительную погрешность
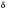 ,
то количество верных знаков
,
то количество верных знаков
 данного числа равно ближайшему целому
числу, заданному формулой
данного числа равно ближайшему целому
числу, заданному формулой
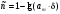 .
.
% Для каждой величины S(Ni) определим количество верных цифр.
% Введем вспомогательный вектор a, который в нашем случае примет вид:
>> a=[1 1 1 1];
% вычисляем количество верных цифр:
>> n=1-log10(a.*d) n = 2.7118e+000 3.7003e+000 4.6991e+000 5.6990e+000
% округлим полученные значения до целых, меньших или равных n:
>> n=floor(n) n = 2 3 4 5
Для записи численных значений найденных частичных сумм, округленных до найденного ранее количества верных цифр необходимы их более точные значения:
>> format long >> S S =
1.47087378640777 1.49700897308076 1.49970008997301 1.49997000089997
% окончательно округляем частичные суммы, оставляя только верные цифры:
|
S1 |
S2 |
S3 |
S4 |
|
1.5 |
1.50 |
1.500 |
1.5000 |
Упражнение 3. а) Используя функцию суммирования symsum(an, n, n1, n2) для n2=inf, установить сходимость рядов 1-6;
б) вычислить
частичные суммы при указанных
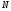 и внести их в таблицу;
и внести их в таблицу;
в) при каждом
из указанных
 вычислить абсолютную погрешность;
вычислить абсолютную погрешность;
г) при каждом
из указанных
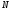 вычислить относительную погрешность
и оценить количество верных цифр и
значение суммы.
вычислить относительную погрешность
и оценить количество верных цифр и
значение суммы.
Указание. В случае, когда частичная сумма выдается в символьном виде, воспользуйтесь командой vpa(ans, m), где m – количество показываемых цифр числа.
1)
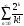 (
(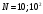 ); 2)
); 2)
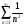 (
( );
);
3)
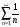 (
(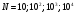 ); 4)
); 4)
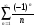 (
(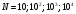 );
);
5)
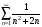 (
(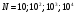 ); 6)
); 6)
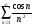 (
(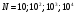 ).
).
Упражнение 4. Вычислить суммы:
1)
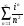 ; 2)
; 2)
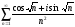 (считает где-то до 1000, поэтому дать
приближенный ответ); 3)
(считает где-то до 1000, поэтому дать
приближенный ответ); 3)
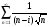 .
.
На дом (повтор из лаб. работы первого курса)
Оценка остатка ряда с положительными членами
|
Для ряда
Утверждение об оценке
остатка ряда. Если для ряда с
положительными членами существует
такое число
|
Для выполнения следующего упражнения, Вам, возможно, понадобится оператор цикла с неопределенным числом операций while … end. Его синтаксис:
while <логическое выражение>
<инструкции>
еnd
Этот оператор многократно выполняет инструкцию или группу инструкций, пока логическое выражение истинно. Логическое выражение имеет форму:
выражение <оператор отношения> выражение
оператор отношения: ==, <=, >=, <, >, ~
Упражнение 1. Пусть к ряду
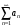 применимо утверждение об оценке ряда.
Создайте M-функцию, которая
оценивает число членов, достаточное
для вычисления суммы ряда с заданной
точностью
применимо утверждение об оценке ряда.
Создайте M-функцию, которая
оценивает число членов, достаточное
для вычисления суммы ряда с заданной
точностью
 ,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметров
M-функции используйте
формулу общего члена последовательности
и точность
,
и вычисляет сумму ряда с заданной
точностью. В качестве входных параметров
M-функции используйте
формулу общего члена последовательности
и точность
 .
Применить созданную М-функцию для
вычисления с точностью до 0,001 суммы
ряда:
.
Применить созданную М-функцию для
вычисления с точностью до 0,001 суммы
ряда:
а)
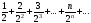 ; б)
; б)
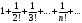
Указание. Для ряда
а) имеем:
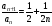 – при увеличении
– при увеличении
 монотонно уменьшается от
монотонно уменьшается от
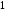 до
до
 .
Для ряда б):
.
Для ряда б):
 – убывает от
– убывает от
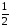 до нуля.
до нуля.
М-функция может содержать два цикла. В
первом цикле, начиная с
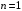 ,
вычисляем
,
вычисляем
 и
и
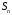 до тех пор, пока выполняется неравенство
до тех пор, пока выполняется неравенство
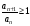 .
.
Во втором цикле продолжаем вычислять
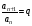 и
и
 ,
а также
,
а также
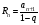 .
Второй цикл заканчивается при выполнении
условия
.
Второй цикл заканчивается при выполнении
условия
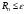 .
Выходными параметрами М-функции должны
быть
.
Выходными параметрами М-функции должны
быть
 и
и
 .
.
Комментарии к работе в комп. зале.
Пример
1.
Найти сумму ряда
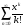 .
.
>> syms k n x v
syms x k
symsum(x^k/sym('k!'), k, 0,inf)
ans = exp(x)
Пример
2.
Найти сумму ряда
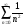 .
.
>> syms n
>> symsum(1/n^2,n,1,inf)
ans = 1/6*pi^2
Пример
3.
Найти сумму ряда
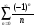 .
.
>> syms n
>> symsum((-1)^n/n,n,1,inf)
ans = -log(2)
Пример
4.
Найти сумму ряда
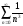 .
.
>> syms n
>> symsum(1/n^3,n,1,inf)
ans =
zeta(3)
>> vpa(ans,8)
ans = 1.2020569
Следовательно, результат выражается через дзета – функцию Римана (справка по этой функции – doc zeta) и равен zeta(3)≈1,2020569.
Пример
5.
Найти сумму ряда
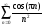 .
.
>> sym s n; symsum(cos(n*pi)/n^2,n,1,inf)
ans =
-hypergeom([1, 1, 1],[2, 2],-1)
>> vpa(ans,8)
ans = -.82246703
Следовательно, результат выражается через гипергеометрическую функцию (справка по этой функции – doc hypergeom) и равен
= -hypergeom([1, 1, 1],[2, 2],-1) ≈ -0,82246703.
Пример
7.
Найти сумму ряда
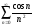 .
.
>> syms n
>> symsum(cos(n)/n^2,n,1,inf)
ans =
polylog(2, 1/exp(i))/2 + polylog(2, exp(i))/2
Следовательно, результат выражается через полилогарифмическую функцию и равен
>> vpa(ans,5)
ans =
0.32414
Использование symsum для доказательства тождеств.
Пример 8. Найти конечную сумму с
переменным верхним пределом для
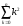
>> syms k
>> symsum(k^2,k,0,10)
ans =
385
>> syms k n
>> symsum(k^2,k,0,n)
ans =
1/3*(n+1)^3-1/2*(n+1)^2+1/6*n+1/6
>> pretty(ans)
3 2
1/3 (n + 1) - 1/2 (n + 1) + 1/6 n + 1/6
Пример 9. Найти конечную сумму с
переменным верхним пределом для
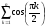 .
.
>> syms k n
>> symsum(cos(k*pi/2),k,1,n)
ans =
1/2*sin(1/2*(n+1)*pi)-1/2*cos(1/2*(n+1)*pi)-1/2
simple(ans)
ans =
1/2*cos(1/2*n*pi)+1/2*sin(1/2*n*pi)-1/2

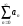 ряд
ряд
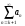 называют
называют
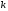 -м
остатком ряда. Если сходится ряд
-м
остатком ряда. Если сходится ряд
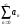 ,
то сходится и его остаток, причем их
суммы связаны соотношением
,
то сходится и его остаток, причем их
суммы связаны соотношением
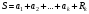 (здесь
(здесь
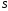 – сумма ряда,
– сумма ряда,
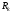 – сумма остатка).
– сумма остатка).
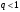 ,
что при всех
,
что при всех
 ,
начиная с некоторого
,
начиная с некоторого
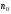 ,
выполняется неравенство
,
выполняется неравенство
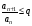 ,
то сумма
,
то сумма
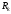
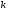 -го
остатка при
-го
остатка при
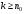 удовлетворяет неравенству
удовлетворяет неравенству
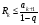 .
.