
- •1.Принцип неопределенности
- •2. Полный набор динамических переменных
- •3. Постулаты квантовой механики
- •4. Волновая функция и ее свойства
- •5. Принцип суперпозиции состояний
- •6. Операторы в квантовой механике
- •Транспонированный оператор
- •7. Собственные функции и собственные значения эрмитовых операторов. Случай дискретного (и непрерывного спектра)
- •8. Операторы координаты , импульса, момента импульса, энергии
- •9. Волновое уравнение
- •10. Оператор Гамильтона различных систем
- •11. Решение волнового уравнения в случае свободной материальной точки
- •12. Собственный механический момент (спин)
- •13. Спиновая переменная волновой функции
- •14. Статистическое описание систем с большим числом степеней свободы
- •14. Два способа усреднения в статистической физике. Понятие ансамбля систем
- •15. Каноническое распределение Гиббса
- •16. Квазиклассическое приближение в статистической физике
- •17. Использование распределения Максвелла для расчёта средних:,,,
- •18. Распределение Ферми-Дирака
- •19. Распределение Бозе-Эйнштейна
14. Статистическое описание систем с большим числом степеней свободы
Статистическая физика изучает системы
с большим числом степеней свободы.
Наличие большого число степеней свободы
вносит некоторые особенности в описание
таких систем. Например, в
 воздуха
содержится
воздуха
содержится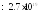 частиц (число Лошмидта), но у каждой
материальной точки (частицы) имеется 3
степени свободы, поэтому у этой системы
огромное число степеней свободы.
частиц (число Лошмидта), но у каждой
материальной точки (частицы) имеется 3
степени свободы, поэтому у этой системы
огромное число степеней свободы.
В классической механике возможно
описывать такие системы (через формализм
Гамильтона) -
 динамических переменных
динамических переменных ,
где
,
где - число степеней свободы. Описание
системы сводится к решению уравнений:
- число степеней свободы. Описание
системы сводится к решению уравнений:
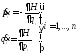
Чтобы решить данную систему, необходимо
задать
 начальных условий. Задаем начальные
условия и решаем систему. Но здесь
сложные технические трудности (долгий
счёт на ЭВМ). Но имеются ещё и качественные
особенности этих систем, которые не
охватываются этими уравнениями, т.е.
детерминированный подход здесь не
используют.
начальных условий. Задаем начальные
условия и решаем систему. Но здесь
сложные технические трудности (долгий
счёт на ЭВМ). Но имеются ещё и качественные
особенности этих систем, которые не
охватываются этими уравнениями, т.е.
детерминированный подход здесь не
используют.
Статистическая физика рассматривает
переход от малого числа степеней свободы
к большому.
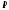 и
и - это динамические переменные. Фазовое
пространство – это
- это динамические переменные. Фазовое
пространство – это мерное пространство, декартовыми осями
которого являются переменные
мерное пространство, декартовыми осями
которого являются переменные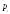 и
и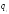 .
Тогда состояние системы (которое задаётся
динамическими переменными) в фазовом
пространстве задаётся фазовой точкой.
Движение системы в реальном пространстве
задаётся движением фазовой точки в
фазовом пространстве, т.е. устанавливается
соответствие между фазовым и реальным
пространствами.
.
Тогда состояние системы (которое задаётся
динамическими переменными) в фазовом
пространстве задаётся фазовой точкой.
Движение системы в реальном пространстве
задаётся движением фазовой точки в
фазовом пространстве, т.е. устанавливается
соответствие между фазовым и реальным
пространствами.
.
14. Два способа усреднения в статистической физике. Понятие ансамбля систем
Будем иметь дело со стационарными процессами.
Рассмотрим случайную величину
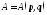 ,
где
,
где и
и это динамические переменные (их
это динамические переменные (их штук). Но можно рассматривать и случайную
величину
штук). Но можно рассматривать и случайную
величину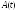 ,
где
,
где - время (это одна переменная).
- время (это одна переменная).
Усреднение по времени производим так:
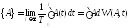 (**)
(**)
Если
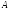 - случайная величина, то её усреднение
соответствует усреднению по фазовой
траектории в фазовом пространстве.
- случайная величина, то её усреднение
соответствует усреднению по фазовой
траектории в фазовом пространстве.
Зависимость координат от времени в фазовом пространстве определяется фазовой траекторией.


Усреднение по времени имеет основой эксперимент, т.к. экспериментатор наблюдает случайную величину во времени.
Назовём
 временем релаксации. Если
временем релаксации. Если ,
то предел (**) хорошо согласуется с
практикой. И тогда принимают
,
то предел (**) хорошо согласуется с
практикой. И тогда принимают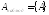 .
.
Усреднение по времени, однако не удобно в теории, это усреднение по одной реализации.
Другое усреднение – статистическое.
Оно основано на усреднении случайной
величины
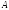 как функции
как функции и
и .
.
Каждой точке фазового пространства
ставится в соответствие величина
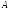 (
как функция
(
как функция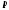 и
и ).
Потом вводится вероятность попадания
этой точки в элементарный объём фазового
пространства:
).
Потом вводится вероятность попадания
этой точки в элементарный объём фазового
пространства:
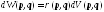
здесь
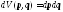 - элементарный объём фазового пространства.
- элементарный объём фазового пространства.
Говорят, что
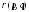 - это функция распределения, определяющая
плотность вероятности попадания точки
в элементарный объём.
- это функция распределения, определяющая
плотность вероятности попадания точки
в элементарный объём.
И вводится понятие статистического среднего, или среднего по ансамблю:
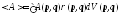
Имеем совокупность макроскопических идентичных систем, именуемых ансамблями. Можем говорить, что конкретная точка фазового пространства соответствует конкретному состоянию одной из систем этого ансамбля.
У систем может быть различное динамическое состояние, так как точки перемещаются в пространстве. Хотя число точек, поля и т.п. у систем будут одинаковыми. Это и будет ансамблем, если таких систем будет неограниченно много.
Часто, т.к. рассматриваются стационарные
процессы, то фазовая траектория очень
длинная (бесконечная), тогда говорят,
что фазовую траекторию, при рассмотрении
предела
 ,
можно разбить на достаточно длинные
траектории, которым можно приписать
системы из ансамбля.
,
можно разбить на достаточно длинные
траектории, которым можно приписать
системы из ансамбля.
