8. Операторы координаты , импульса, момента импульса, энергии

Будем использовать координатное представление (- представление). Будем рассматривать систему из одной материальной точки. Действие сводится к умножению на вектор, т. е.(это определение действия оператора).

Здесь строго соблюдается последовательность операторов при раскрытии векторного произведения, например, первая компонента:

,

однако для частного случая декартовых координат порядок операторов не существенен.

Оператор энергии или гамильтониан :

,

здесь - оператор кинетической энергии,- оператор потенциальной энергии. Для одной материальной точки гамильтониан имеет вид:

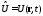
Переменная t – признак внешнего нестационарного поля.

Тут присутствует и, ноиодновременно неизмеримы, тогда потенциальная и кинетическая энергия в квантовой механике не могут быть одновременно измеримыми. В квантовой механике существует понятие “энергия частицы”, но порознь вводить энергию нельзя, иначе либо, либооказываются неизвестными.

9. Волновое уравнение

Надо сформулировать уравнение функции, которая описывала бы квантово-механическую систему.

Это уравнение было получено Шредингером интуитивным путем. Оно ниоткуда не выводится.

Приведем некоторые соотношения в пользу уравнения Шредингера:

Норма волновой функции:

- вероятность обнаружить динамические переменные в интервале.

Наложим на - условие ее сохранения во времени.- это физическое требование, поскольку, тотакже функция времени.

На базе ограничения получим некоторые ограничения на.

Обозначим . Мы знаем, что, таким образом. Тогда само скалярное произведение- чисто мнимое число.

Но - число вещественное. Отсюда можно представить

(19.1)

Здесь мнимая единица из соотношения . Т. к. в (*) стоит линейный оператор, то это соотношение удовлетворяет принципу суперпозиции.

Подставим (19.1) в равенство , тогда

- эта величина должна быть чисто вещественной, тогда оператор- эрмитов:.

Свойства оператора :

В пределе перехода к классической механике: , то, гдеS – действие из классической механики. Причем, тогда рассматривая

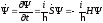, (19.2)

где - функция Гамильтона.

В нашем случае , тогда учитывая предельный переходи (19.2), то:.

Получили волновое уравнение:

- нестационарное уравнение Шредингера (волновое уравнение).

Каждой системе ставится в соответствие Гамильтониан, решаем с гамильтонианом уравнение Шредингера и получаем волновую функцию которая определяет эволюцию системы.

10. Оператор Гамильтона различных систем

Этот вопрос идентичен вопросу рассмотренному в классической механике - будут те же соотношения, но для операторов

.

Поставим в соответствие конкретной системе операторы и:

В декартовой системе координат ,.

Здесь n– число точек в системе.

.

- функция от оператора координаты.

Мы рассматриваем - представление, здесь

Мы рассматриваем декартову систему координат. Гамильтониан мы поставили в соответствие системе материальных точек. Эта система незамкнутая, т. к. потенциальная энергия зависит от времени. (т. е. здесь нет однородности времени).

Перейдем к более простой задаче. Рассмотрим систему N материальных точек во внешнем стационарном поле

Здесь отвечает за внутреннее взаимодействие между частицами.

отвечает за внешнее воздействие на систему частиц.

.

Выражение, описывающее внешнее воздействие обладает аддитивностью, т. е.

.

Индекс a означает, что разные частицы могут взаимодействовать с внешним полем по разному закону. Если все частицы одинаковые и одинаково взаимодействуют с внешним полем, то индексa убирается.

Внутреннее взаимодействие неаддитивно.

Рассмотрим случай свободной материальной точки. Соответственно она ни с чем не взаимодействует:

Тогда , или в-представлении, то

,

тогда .

Если материальная точка во внешнем поле:

,,

Нестационарное поле .

Стационарное поле .

Центральное поле .

Рассмотрим систему двух материальных точек. Мы рассматриваем частный случай – замкнутая система двух материальных точек.

В случае классической механики: .

Отсутствие t в энергии взаимодействия – это однородность времени и закон сохранения энергии.

Зависимость энергии от модуля есть изотропность пространства.

В квантовой механике в -представлении:

,

,

где