1.2. Несколько слов о системах единиц

Мы будем пользоваться международной системой единиц (СИ), о недостатках которой можно почитать в литературеСивухин Д.В. ОБЩИЙ КУРС ФИЗИКИ, том 3 "Электричество", часть 2 , М., "Наука", 1996. §85

Основные единицы этой системы:

Метр (м), килограмм (кг),секунда (с), Кельвин (к) и Ампер (а)

При этом величина заряда и сила определяются независимо друг от

друга: сила из второго закона Ньютона, а заряд из величины тока

1 заряда (Кулон) = 1Кл = 1 А1 с

Коэффициент k (постоянная в законе Кулона) является размерной величиной и равен:

, где

- электрическая постоянная. Будет введена нами и - магнитная постоянная. Эти постоянные никакого реального физического смысла не имеют, являясь размерными коэффициентами, искусственно введенными для перехода величин (о которых мы также будем говорить в дальнейшем)Е, D, B, H,в вакууме из одних единиц в другие, однако комбинацияимеет реальный физический смысл, где скорость света должна измеряться в м/c.

Запишем некоторые другие важные соотношения: ; гдеФ– (фарад) единица электрической емкости, в единицахГн(генри)- измеряется индуктивность.

1.3.Напряженность электрического поля (м. Фарадей 1850 г)

Согласно современным представлениям, электромагнитное взаимодействие между телами осуществляется посредством поля. (Это представление лежит в основе так называемой классической электродинамики, к изучению которой мы приступаем. В квантовой теории все силы природы возникают в результате обмена частицами-переносчиками между взаимодействующими частицами. В случае электромагнитного взаимодействия такими частицами-переносчиками являются фотоны - кванты электромагнитного поля).

Определение заряда и напряженности электрического поля, как и любых других физических величин, сводится к указанию принципиального способа их измерения. Так как электромагнитные явления связаны с действием сил на заряженные тела, то именно силы могут быть положены в основу этих определений.

Для изучения действия сил на заряженные тела будем использовать пробный заряд.

Пробным зарядом называется электрически заряженное тело, удовлетворяющее следующим требованиям:

1) величина заряда должна быть настолько мала, чтобы практически не приводить к перераспределению электрического заряда на телах, поле которых исследуется с помощью пробного заряда;

2) размеры пробного заряда должны быть настолько малы, чтобы все его части были погружены в точки, где исследуемое поле одинаково (т.е. в области, занимаемой телом пробного заряда, исследуемое поле однородно).

Заряды, удовлетворяющие второму условию, называются точечными.

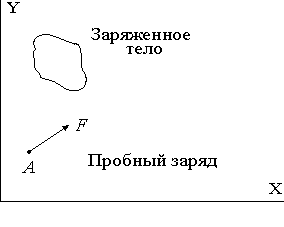
Рис.1.1. Действие заряженного тела на неподвижный в системе отсчета XY пробный заряд

Возьмем два таких пробных заряда и поместим их по очереди в одну и ту же точку пространства так, чтобы они покоились в соответствующей инерциальной системе отсчета (рис.1.1). Пусть и - силы, с которыми заряженные тела действуют на эти неподвижные пробные заряды. Обобщением опытных фактов является следующее утверждение: силы и имеют либо одинаковые, либо противоположные направления, а отношение их величинF₁/F₂не зависит от выбора точки наблюдения (т.е. точки расположения пробного заряда). Поэтому ясно, что отношениеF₁/F₂служит мерой самих пробных зарядов, а не действия заряженных тел, и состояние электризации пробного заряда можно охарактеризовать скалярной величиной , определив его как

(1.1)

Из этого уравнения следуют два важных вывода:

1) приняв заряд какого-либо пробного тела за положительный единичный, из (1.1) можно найти величину второго заряда;

2) помещая данный пробный заряд q₁(например, тот, который выбран за положительную единицу) в разные точки пространстваА,В,С, ... и измеряя силы , действующие на него, когда он неподвижен, можно с помощью (1.1) определить силы , с которой будут действовать заряженные тела на любой другой неподвижный пробный зарядq₂, помещаемый в эти точки. В самом деле, .

Другими словами, множество сил, действующих на единичный неподвижный пробный заряд во всех точках пространства данной системы отсчета, является силовым полем, которое в то же время предопределяет силу, действующую на любой другой заряд, неподвижный в этой системе отсчета.

Для описания силовых свойств электрического поля вводится напряженность электрического поля .

Векторная физическая величина, модуль которой численно равен силе, действующей на единичный положительный неподвижный пробный заряд, помещенный в некоторой точке наблюдения, а направление совпадает с направлением этой силы, называется напряженностью электрического поля в рассматриваемой точке наблюдения и обозначается вектором ,

(1.2)

Силу, действующую на любой другой заряд q, покоящийся в поле , на основании (1.1) и (1.2), представим в следующем векторном виде:

Неподвижность заряда qочень существенна, так как электромагнитное взаимодействие зависит не только от заряда тела, но и от скорости его движения. Электрическое же (а не электромагнитное) поле полностью описывает взаимодействие зарядов только по отношению к таким системам отсчета, где заряженные тела неподвижны.