45

Лекция 3.

2. Потенциал электростатического поля.

(«Пионером» в этой области считается Лагранж, который

в 1777 году впервые ввел понятие потенциала для гравитационного поля).

2.1. Работа сил электростатического поля по переносу точечного заряда.

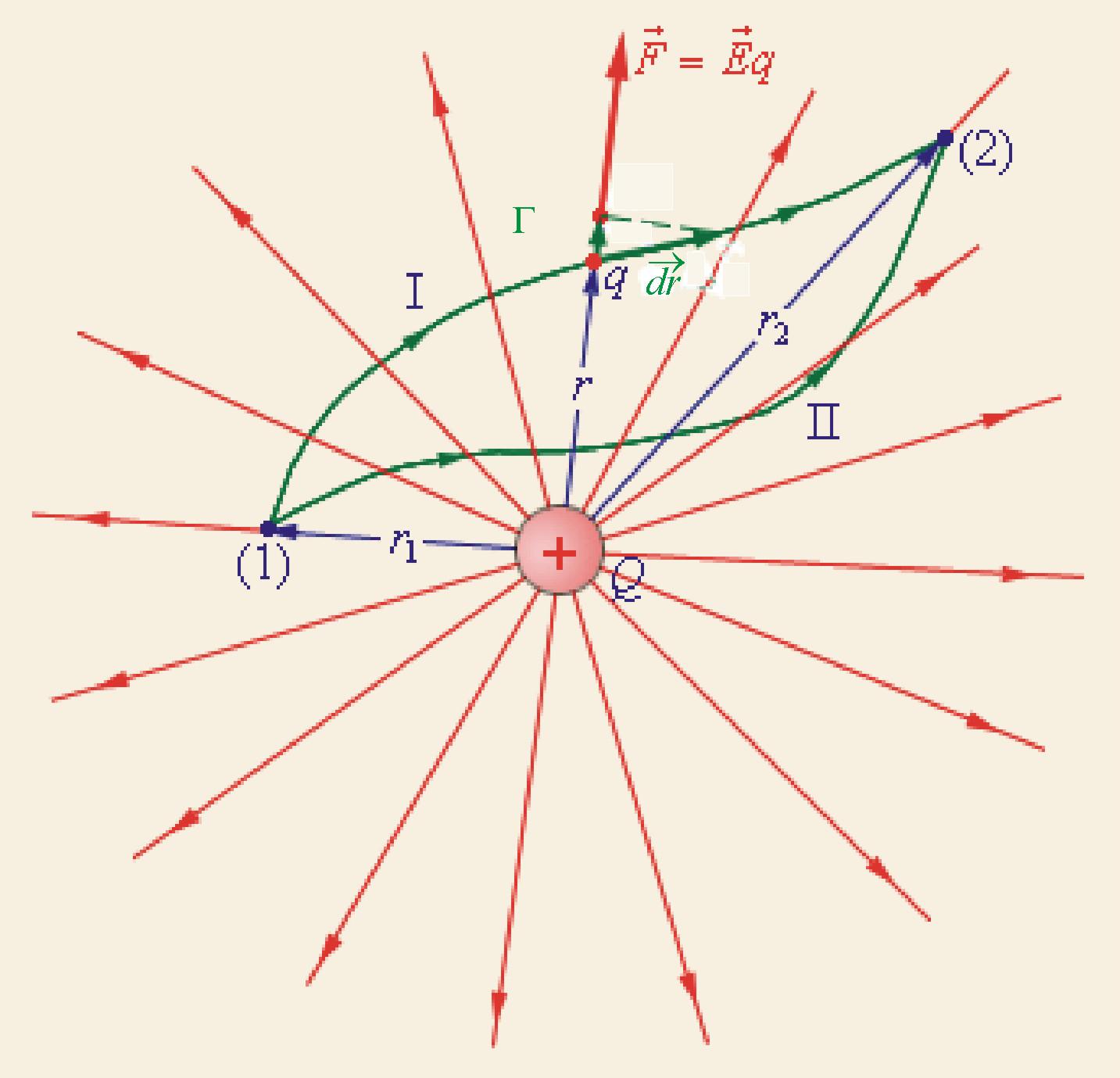
Пробный (положительный и очень маленький по размеру – это определение пробного заряда) заряд q медленно (квазистатически – заряд находится почти в покое) перемещаем по пути Г («гамма-большое») из 1 в 2 в электростатическом поле точечного статического заряда Q. Найдем элементарную работу сил электростатического поля этого заряда по перемещению заряда q:

Как известно из курса механики

Элементарная работа силы : где – элементарное перемещение точки приложения силы .

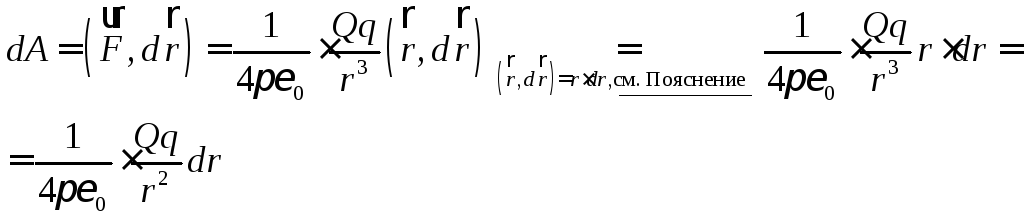
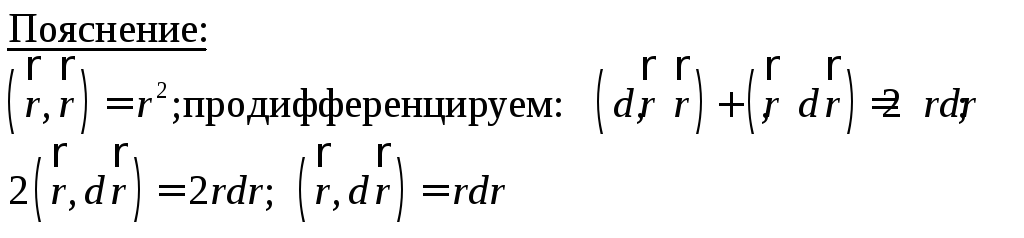Итак, работа сил электростатического поля по перемещению точечного заряда из положения 1 в положение 2 по контуру Г может быть вычислена по формуле:

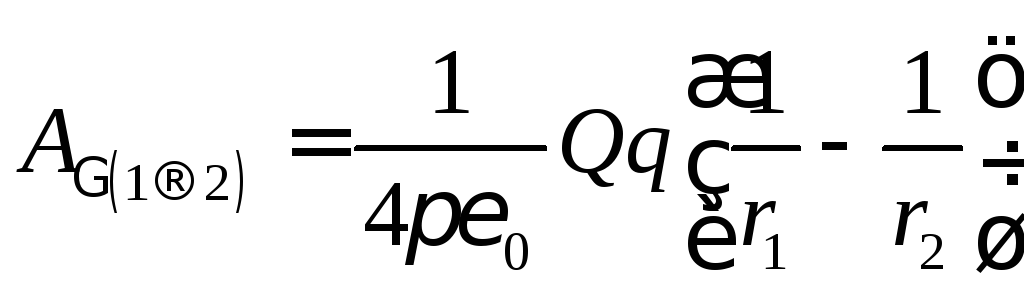(1)

2.2. Интегральный признак потенциальности электростатического поля.

Анализируя полученную формулу для работы сил электростатического поля по перемещению заряда q по некоторому контуру Г, можно сделать следующие выводы:

1. работа 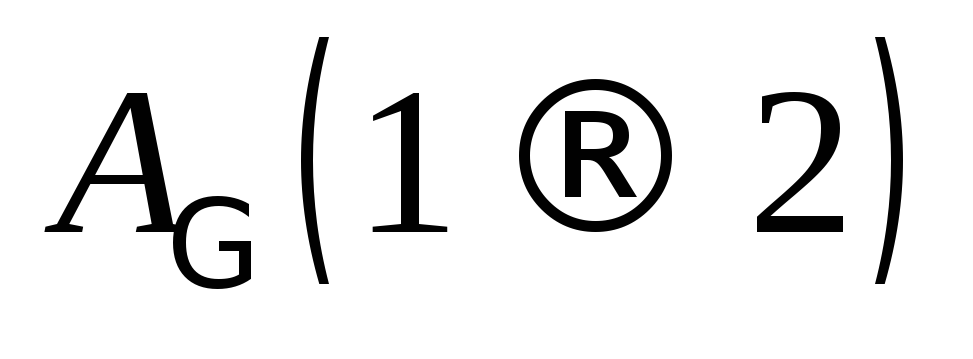не зависит от формы контура Г, а зависит только от начального и конечного положений;

2. если точки 1 и 2 совпадают (контур Г – замкнутый), то 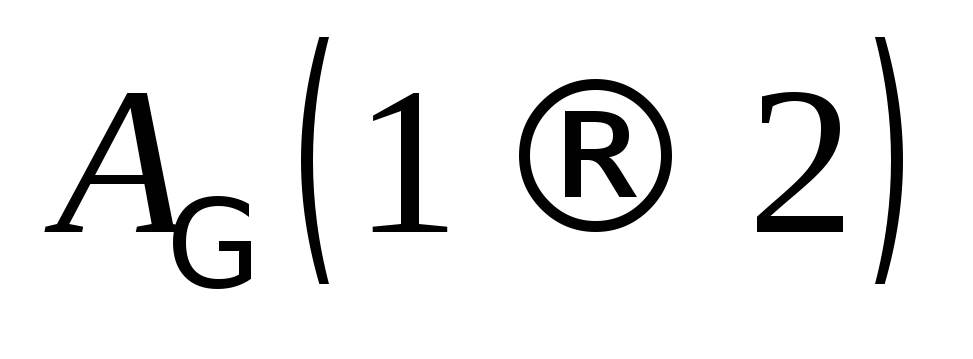=0, т.е.

Линейный интеграл, взятый по замкнутому контуру (замкнутой кривой) Г, называется циркуляцией вектора . Т.е. утверждается, что циркуляция электростатического поля равна нулю.(Теорема о циркуляции).

Последний результат справедлив и для электростатического поля, созданного любой системой покоящихся точечных зарядов, т.к. по принципу суперпозиции электростатических полей

Векторное поле называется потенциальным, если циркуляция этого вектора по любому замкнутому контуру равна нулю.

Однако этот критерий потенциальности является неудобным на практике, т.к. нужно будет исследовать всевозможные контуры (что само по себе невозможно), и установить, является ли интеграл по ним равным нулю.

2.3. Локальный (дифференциальный) признак потенциальности электростатического поля.

Найдем циркуляцию векторапо бесконечно малому плоскому прямоугольному контуру, расположенному в районе некоторой точки, в декартовой системе координат. Нас будет интересовать конфигурация (линейные размеры) этого контура, поэтому изобразим его достаточно большим. Выберем направление обхода по контуру – против часовой стрелки.

Т.к. величины dx и dy являются очень маленькими, можно считать, что и поле на протяжении этих отрезков также одинаково; будем обозначать поле в каждой точке стороны 1 как , поле в каждой точке стороны 2 как, и так далее. Интеграл по замкнутому контуру в данном случае мы можем заменить на сумму четырех слагаемых:

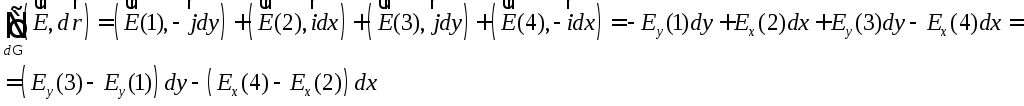
Теперь заметим, что выражение по сути является приращениемy-ковой составляющей поля при переходе из 1 в 3 вдоль оси x. Тогда наше выражение приблизительно равно:

Мы нашли циркуляцию вектора по элементарному контуру.

Аналогично для элементарных прямоугольных контуров в плоскостях yz и zx можно получить:

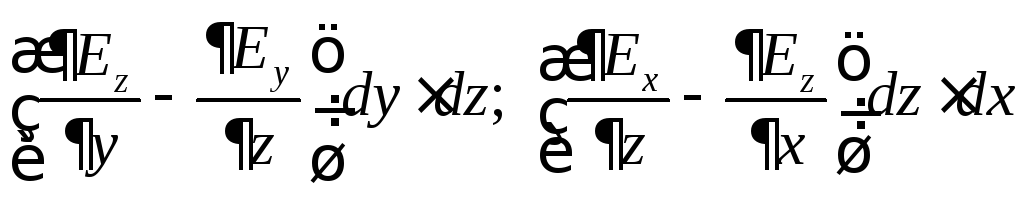
А так как циркуляция вектора по любому контуру равна нулю, то можно сделать вывод, что в потенциальном поле выполняются одновременно все 3 следующих равенства:

(*)

То, что выписано – необходимый, а в электростатике – и достаточный признак потенциальности электрического поля в декартовой системе координат.

Выполнение этих равенств проверить на практике гораздо проще, чем проверять интегральный признак потенциальности электростатического поля.

Итак, полеявляется потенциальным в области, если условия (*) выполняются в каждой точке этой области.

Условия (*)можно компактно записать в векторной форме, если ввести в рассмотрение вектор "ротор" напряженности электрического поля (см. Замечание).

Замечание

Ротор вектораопределим следующим образом

Векторное произведение вектора оператора градиента и вектора напряженности электрического поля, или роторможно записать через детерминант

Следовательно, для электростатического поля имеем