
- •Лекция 4
- •3.Теорема Гаусса Теорема Гаусса (сформулирована для электростатического поля в 1830г.)
- •3.1. Поток вектора через поверхность.
- •Замечания.
- •3.2. Теорема Гаусса в интегральной форме.
- •3.3. Локальная (дифференциальная) форма теоремы Гаусса.
- •Замечание
- •3.4. Дивергенция поля в декартовой системе координат.
- •3.5. Примеры (задача на применение теоремы Гаусса).
- •Другие примеры см. Орокс Тема 2 « Теорема Гаусса», «Примеры решения задач» №2.1-2.14 Например, 2.6.Электрическое поле заряженной плоскости и т.Д.
- •Все разобрать!!!
- •Вычисление по известному потенциала
- •3.8. Уравнения Пуассона (1812 г) и Лапласа (1782 г).
- •Сводка формул к Лекции 3
Лекция 4
3.Теорема Гаусса Теорема Гаусса (сформулирована для электростатического поля в 1830г.)
(1777-1855 – годы жизни Гаусса)

3.1. Поток вектора через поверхность.
Определим элементарный поток через элементарную поверхность:

Рис.1
Чтобы с помощью
линий напряженности можно было
характеризовать не только направление,
но и значение напряженности
электростатического поля их проводят
с определенной густотой: число линий
напряженности, пронизывающих единицу
площади поверхности, перпендикулярную
линиям напряженности, должно быть равно
модулю вектора
![]() .
.
Число линий
напряженности, пронизывающих элементарную
площадку
![]() равно
равно![]()
Величина
![]()
![]() - вектор элементарной
площадки, который может быть определен
по следующей формуле:
- вектор элементарной
площадки, который может быть определен
по следующей формуле:
![]() ,
где
,
где
![]() - вектор нормали к поверхности.
- вектор нормали к поверхности.
![]() «Фи» -поток вектора
«Фи» -поток вектора
![]() через произвольную замкнутую поверхность
через произвольную замкнутую поверхность![]() .
.
Замечания.
С потоком вектора
 не
связано никакое реальное течение
материи.
не
связано никакое реальное течение
материи.

Рис.2. Две возможные ориентации нормали к элементу поверхности
2. Единичный вектор
![]() к
площадке можно ориентировать в двух
противоположных направлениях (рис.2).
Одно из них условно принимается за
положительное, в этом направлении и
проводится нормаль
к
площадке можно ориентировать в двух
противоположных направлениях (рис.2).
Одно из них условно принимается за
положительное, в этом направлении и
проводится нормаль![]() ,
т.е. сторона площадки, из которой исходит
нормаль
,
т.е. сторона площадки, из которой исходит
нормаль![]() ,
называется внешней, а противоположная
ей - внутренней.
,
называется внешней, а противоположная
ей - внутренней.
3. Размерность потока электрического поля следующая:
![]()
Наконец, рассмотрим
свойство аддитивности потока вектора.
В силу принципа суперпозиции вектор
![]() ,
описывающий электрическое поле системы
зарядов, в каждой точке пространства
представляется векторной суммой:
,
описывающий электрическое поле системы
зарядов, в каждой точке пространства
представляется векторной суммой:
![]() ,где
,где
![]() -
вектор напряженности поля, создаваемогоi-м
зарядом в той же точке наблюдения.
-
вектор напряженности поля, создаваемогоi-м
зарядом в той же точке наблюдения.
Умножая это
соотношение скалярно на
![]() и
вводя
и
вводя![]() поток
поляi-го
заряда через ту же самую поверхность
поток
поляi-го
заряда через ту же самую поверхность
![]() получим
получим
![]()
т.е. из того факта,
что векторы поля
![]() складываются
геометрически, следует, что их потоки
через одну и ту же поверхность складываются
алгебраически (принцип аддитивности
потоков).Рис.2
складываются
геометрически, следует, что их потоки
через одну и ту же поверхность складываются
алгебраически (принцип аддитивности
потоков).Рис.2
3.2. Теорема Гаусса в интегральной форме.
Рассмотрим
элементарную площадку
![]() ,
находящуюся в поле, созданном точечным
источникомq,
расположенным в точке наблюдения. Вектор
нормали к площадке
,
находящуюся в поле, созданном точечным
источникомq,
расположенным в точке наблюдения. Вектор
нормали к площадке ![]() не совпадает с
вектором напряженности поля в этой
точке,
не совпадает с
вектором напряженности поля в этой
точке, ![]() - угол между вектором
нормали к поверхности и вектором
напряженности поля; r
– расстояние от источника поля до
площадки. Рассмотрим площадку
- угол между вектором
нормали к поверхности и вектором
напряженности поля; r
– расстояние от источника поля до
площадки. Рассмотрим площадку
![]() ,
элементы которой перпендикулярны r.
Найдем поток через площадку
,
элементы которой перпендикулярны r.
Найдем поток через площадку ![]() :
:

![]()
Введем понятие телесного угла:

Количественной мерой плоского угла является отношение длины дуги l к ее радиусу R. При этом центр кривизны находится в вершине угла.
![]()
Количественной мерой телесного угла является отношение площади поверхности фрагмента сферы, вырезаемой конусом с вершиной в центре сферы. К квадрату радиуса этой сферы.
![]()
Таким образом, в
наших обозначениях![]() - телесный угол.
- телесный угол.
Это пространственный угол, под которым из точки расположения точечного
заряда видна
площадка
![]() (или
(или![]() - они видны под одним и тем же углом).
- они видны под одним и тем же углом).
Тогда выражение для элементарного потока принимает вид:
![]()
Угол
![]() положителен, если площадка
положителен, если площадка![]() обращена к заряду внутренней стороной,
и отрицателен, если внешней.
обращена к заряду внутренней стороной,
и отрицателен, если внешней.
Рассмотрим 2 случая.
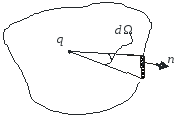 Пусть
заряд q
расположен внутри некоторой замкнутой
поверхности (контур, изображенный на
рисунке, - след от пересечения нашей
поверхности с плоскостью листа). Мы
будем пользоваться понятием внешней
нормали
Пусть
заряд q
расположен внутри некоторой замкнутой
поверхности (контур, изображенный на
рисунке, - след от пересечения нашей
поверхности с плоскостью листа). Мы
будем пользоваться понятием внешней
нормали
 ,
которая направлена из части пространства,
охватываемой поверхностью, наружу. Мы
рассматриваем как раз тот случай, когда
элементарная площадка обращена к заряду
внутренней стороной, т.е. угол
,
которая направлена из части пространства,
охватываемой поверхностью, наружу. Мы
рассматриваем как раз тот случай, когда
элементарная площадка обращена к заряду
внутренней стороной, т.е. угол
 – положительное число. Найдем поток
вектора напряженности через нашу
поверхность. Так как поток – величина
аддитивная, полный поток равен сумме
элементарных потоков:
– положительное число. Найдем поток
вектора напряженности через нашу
поверхность. Так как поток – величина
аддитивная, полный поток равен сумме
элементарных потоков:
![]()
П олный
телесный угол =
олный
телесный угол =![]() .
Для того чтобы в этом убедиться,
представим, что в точке расположения
заряда находится сфера (на рисунке, на
правом экране, она–розовая, радиусом
.
Для того чтобы в этом убедиться,
представим, что в точке расположения
заряда находится сфера (на рисунке, на
правом экране, она–розовая, радиусом![]() )и запишем отношение полной поверхности
сферы
)и запишем отношение полной поверхности
сферы![]() к квадрату ее радиуса
к квадрату ее радиуса![]() .
Получим как раз
.
Получим как раз![]() .
.
Итак, мы получили, что в случае, когда заряд находится внутри замкнутой поверхности, поток поля этого заряда через поверхность
![]()
Теперь рассмотрим случай, когда заряд находится вне рассматриваемой замкнутой поверхности. Из точки наблюдения, в которой расположен заряд, поверхность видна под телесным углом
 .
На рисунке верхней части поверхности
соответствует внешняя нормаль
.
На рисунке верхней части поверхности
соответствует внешняя нормаль  ,
и телесный угол, соответствующий этой
части поверхности, будет иметь знак
«+». Нижней же части поверхности
,
и телесный угол, соответствующий этой
части поверхности, будет иметь знак
«+». Нижней же части поверхности
соответствует
внешняя нормаль ![]() ,
телесный угол, соответствующий этой
части поверхности, будет иметь знак
«-». Тогда полный поток, пронизывающий
нашу поверхность, может быть представлен
в виде суммы двух потоков:
,
телесный угол, соответствующий этой
части поверхности, будет иметь знак
«-». Тогда полный поток, пронизывающий
нашу поверхность, может быть представлен
в виде суммы двух потоков:
![]() ,
где
,
где
![]() - поток через верхнюю часть поверхности,
- поток через верхнюю часть поверхности,![]() - поток через нижнюю часть нашей
поверхности. Распишем это выражение,
учитывая, что поверхность со знаком «+»
и поверхность со знаком «-» опираются
на телесные углы равные по величине, но
противоположные по знаку:
- поток через нижнюю часть нашей
поверхности. Распишем это выражение,
учитывая, что поверхность со знаком «+»
и поверхность со знаком «-» опираются
на телесные углы равные по величине, но
противоположные по знаку:
![]()
Т.е. получаем, что в случае, когда заряд находится вне замкнутой поверхности, поток этого заряда через поверхность = 0.

Мы рассмотрели
только случай, когда поле создается
единственным точечным зарядом. Если же
поле создается системой точечных
зарядов, то поток поля
![]() ,
проинтегрированный по всей замкнутой
поверхности, в силу принципа суперпозиции
может быть представлен в виде:
,
проинтегрированный по всей замкнутой
поверхности, в силу принципа суперпозиции
может быть представлен в виде:
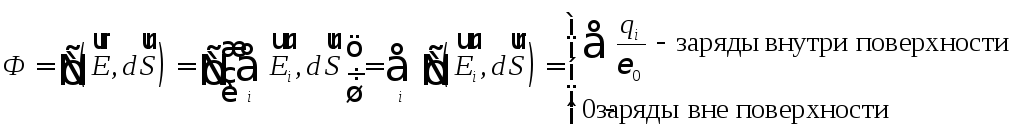
Замечание.
Подчеркнем, что речь идет только о замкнутой поверхности, поэтому на значке интеграла ставим кружочек. Также речь идет только о том заряде, который расположен внутри замкнутой поверхности, не на и не вне.
Случай, когда точечный заряд q находится на самой поверхности S, рассматривать не имеет смысла. Дело в том, что расстояние от точечного заряда до точек пространства, в которых он создает поле, должно быть велико по сравнению с размерами этого заряда. Это требование не выполняется для точек поверхности, на которой расположен точечный источник поля.
Однако поле
![]() создается не только тем зарядом, который
попал в гауссову поверхность, а вообще
всеми зарядами. Поток же поля определяется
только теми зарядами, которые попали
внутрь гауссовой поверхности.
создается не только тем зарядом, который
попал в гауссову поверхность, а вообще
всеми зарядами. Поток же поля определяется
только теми зарядами, которые попали
внутрь гауссовой поверхности.
![]() - интегральная
форма теоремы Гаусса.
- интегральная
форма теоремы Гаусса.
Таким образом,
электростатическая
теорема Гаусса утверждает:
поток поля
![]() через произвольную замкнутую поверхность
равен отношению алгебраической величины
суммарного заряда внутри этой поверхности
к
через произвольную замкнутую поверхность
равен отношению алгебраической величины
суммарного заряда внутри этой поверхности
к![]() .
.
