
- •9. Несобственные интегралы. Признаки сравнения.
- •10. Несобственные интегралы c особенностями в нескольких точках.
- •11. Функции многих переменных
- •17. Свойства функций, непрерывных на замкнутом промежутке
- •18. Понятие локального экстремума. Необходимые условия.
- •19.Достаточные условия локального экстремума.
- •№27. Численные методы вычисления определённого интеграла
№1.Понятие первообразной и неопределенного интеграла. Свойства. Таблица интегралов.
Функция F(x) называется первообразной для функции f(х) на (a,b), если F(x) дифференцируема на (a,b) и F`(x)=f(x).
Произвольная первообразная для f(х) на (a,b) называется неопределенным интегралом от функции f (x)
Функция f (x) называется подынтегральной функцией, дифференциал f (x) dx – подынтегральным выражением, переменная x – переменной интегрирования, а C – постоянной интегрирования
Свойства:
1.d∫f(x)dx=f(x)dx
2. ∫dF(x)=F(x)+c
3. ∫Af(x)dx=A∫f(x)dx+c
4. ∫(f(x)+g(x))dx=∫f(x)dx+∫g(x)dx
5. ∫f(ax+b)dx=1/a F(ax+b)+c
Таблица интегралов.
∫0dx=c
∫ xαdx=
 ,
α ≠ –1
,
α ≠ –1∫

∫
 ,
a
,
a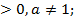
∫
 +c
+c∫

∫

∫
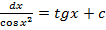
∫

10.∫![]()
11.∫![]()
12.∫![]() – длинный логарифм
– длинный логарифм
13.∫![]() - высокий логарифм
- высокий логарифм
№2. Методы замены и интегрирования по частям для неопределенного интеграла.
Метод замены переменной. ∫f(x)dx=∫f(φ(t))*φ`(t)dt; x=φ(t) – дифференцируемая функция.
Доказательство.
![]()
Метод интегрирования по частям. Пусть U(x) и V(x) дифференцируемые функции. Тогда по свойству дифференциала d(uv)=vdu+udv.
![]() ;
;
![]() .
.
№3. Понятие определенного интеграла. Геометрический и экономический смысл определенного интеграла.

Опр.
Предел
интегральной суммы при λ→0, если он
существует, называется определенным
интегралом от функции f(x)
на [a,b].
![]() .
.
Геометрический
смысл. Пусть
f(x)
неотрицательна на [a,b],
тогда ![]() равен площади фигуры ограниченной
сверху графиком функции f(x),
снизу Ox.
равен площади фигуры ограниченной
сверху графиком функции f(x),
снизу Ox.
Экономический
смысл. Пусть
Z=f(x)
– производительность труда, тогда объем
продукции, произведенный за время T
будет равен ![]() .
.
№4. Свойства определенного интеграла
1)
![]()
Док-во:
![]()
2)
![]()
Док-во:
![]()
3)
a<c<b
![]()
4)
![]()
![]()
5)
![]()
![]()
Док-во:
по свойству 4) ![]()
![]() ;
;
![]() ;
;
![]()
6) Теорема о среднем значении
Если
f(x)
непрер. на [a,b],
то
![]()
![]() [a,b]:
[a,b]:
![]()
Док-во:
f(x)
непрерыв. => ![]()
![]() ;
;
![]()
7)
![]()
№5. Определенный интеграл с переменным верхним пределом.
Ф(х)=![]() ;
Xє[a;b],
f(x)
интегрирована на [a;b].
;
Xє[a;b],
f(x)
интегрирована на [a;b].
![]()
Теорема.
Пусть f(x)
непрерывна на [a;b].
Тогда ![]() хє[a;b]
Ф`(x)=f(x).
хє[a;b]
Ф`(x)=f(x).
Доказательство. Ф(х+∆х)=Ф(х)+f(ξ)∆x, ξє[x,x+∆x]
![]() =f(ξ)
=f(ξ)
![]() =
=![]()
№6. Формула Ньютона-Лейбница.
Теорема.
Пусть f(x)
непрерывна на [a;b].
F(x)-любая
первообразная для f(x)
на [a;b].
Тогда ![]() =F(b)-F(a)
=F(b)-F(a)
Доказательство.
Ф(х)=![]() ,
Ф(х)-первообразная для f(x).
F(x)=Ф(х)+c,
c=const. F(b)-F(a)=(Ф(b)+c)-(Ф(a)+c)=Ф(b)-Ф(а)=
,
Ф(х)-первообразная для f(x).
F(x)=Ф(х)+c,
c=const. F(b)-F(a)=(Ф(b)+c)-(Ф(a)+c)=Ф(b)-Ф(а)=![]() -
-![]() =
=![]() .
.
Замена переменной в определенном интеграле, интегрирование по частям.
Теорема
(замена переменных).Пусть
φ(t)
имеет непрерывную производную на [α;β],
a=φ(α),
b=φ(β),
f(x)
непрерывна ![]() х=φ(t),
tє[α,β].
Тогда
х=φ(t),
tє[α,β].
Тогда ![]() .
.
Доказательство. Пусть F(x) и Ф(х) первообразные для f(x) и f(φ(t))*φ`(t). Ф(t)=F(φ(t))+c, tє[α,β]. Ф(β)-Ф(α)=(F(φ(β))+c)-(F(φ(α))+c)=F(b)-F(a).
Теорема(интегрирование
по частям).
Пусть u=u(x)
и v=v(x)
имеют непрерывную производную на [a,b].
Тогда ![]() |
|![]() .
.
Доказательство.
![]() |
|![]() =
=![]()
№7. Применение определенного интеграла к вычислению:
площади криволинейной фигуры Площадь фигуры, ограниченной графиками непрерывных функций y=f1(x) и y=f2(x), f1(x)≤f2(x) и двумя прямыми x=a и x=b определяется по формуле

длины дуги Если гладкая кривая задана уравнением y=f(x), то длина ее дуги равна
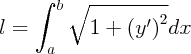 где
a
и b
– абсциссы концов дуги
где
a
и b
– абсциссы концов дугиобъема тела вращения Объем тела вращения, ограниченного поверхностью вращения кривой f(x) вокруг оси Ox и плоскостями x=a, x=b вычисляется по формуле
 Если
вращение вокруг оси Oy
кривой x=g(y)
то
Если
вращение вокруг оси Oy
кривой x=g(y)
то

площади поверхности вращения Площадь поверхности, образованной вращением вокруг оси Ox дуги кривой, заданной функцией y=f(x), a≤x≤b, вычисляется по формуле

№8. Несобственные интегралы. Критерий Коши сходимости несобственного интеграла.
Пусть
f(x)
непрерывна на любом отрезке
![]() . Тогда
. Тогда
![]() называется
несобственным интегралом I
рода.
Если предел существует и он конечен, то
несобственный интеграл сходящийся;
если предел не существует или он
бесконечен то интеграл расходящийся.
называется
несобственным интегралом I
рода.
Если предел существует и он конечен, то
несобственный интеграл сходящийся;
если предел не существует или он
бесконечен то интеграл расходящийся.
Если
f(x)
непрерывна на любом отрезке
![]() ,
,
![]() .
Тогда
.
Тогда
![]() называется несобственным интегралом
II
рода.
Если предел существует и он конечен, то
несобственный интеграл сходящийся;
если предел не существует или он
бесконечен то интеграл расходящийся.
называется несобственным интегралом
II
рода.
Если предел существует и он конечен, то
несобственный интеграл сходящийся;
если предел не существует или он
бесконечен то интеграл расходящийся.
Несобственные интегралы I и II рода называются интегралом с единственной особенностью.
Критерий Коши сходимости несобственных интегралов:
Для сходимости несобственного интеграла с единственной особенностью в точке b необходимо и достаточно чтобы.
![]()
Доказательство.
Рассмотрим
функцию
![]() ,
a<x<b.
По критерию Коши для предела функции
,
a<x<b.
По критерию Коши для предела функции
![]()
![]() ,
чтд
,
чтд
9. Несобственные интегралы. Признаки сравнения.
1). Интеграл по бесконечной области
f(x,y)
непрерывна в бесконечной области D
![]() , где D’-
конечная область лежащая в D,
кот. расширяется произвольным образом.
Если существует конечный предел, не
зависящий от выбора области D’
и способа расширения, то несобственный
интеграл называется сходящимся.
, где D’-
конечная область лежащая в D,
кот. расширяется произвольным образом.
Если существует конечный предел, не
зависящий от выбора области D’
и способа расширения, то несобственный
интеграл называется сходящимся.
2). Интеграл от разрывной функции
Пусть f(x,y) непрерывна в огр. замкнутом D всюду, за исключением P0(x0,y0).
Если
существует конечный предел ![]() , где De
– это область D
с вырез. E-окружностью
точки P0,
то этот предел называется несобственным
интегралом от функции f(x,y)
по области D.
, где De
– это область D
с вырез. E-окружностью
точки P0,
то этот предел называется несобственным
интегралом от функции f(x,y)
по области D.
Интеграл Пуассона
![]()
Признак сравнения.
Пусть
функции f(x)
и g(x)
интегрируемы по любому отрезку [a,b]
и при х ≥ a
удовлетворяют
неравенствам 0 ≤ f(x)
≤ g(x).
Тогда:
![]() если
сходится интеграл
если
сходится интеграл
![]() ,
то сходится интеграл
,
то сходится интеграл
![]() ;
;
![]() если
расходится интеграл
если
расходится интеграл
![]() ,
то расходится интеграл
,
то расходится интеграл
![]()
Док-во:
если
0≤f(x)
, 0≤g(x),
то функции
![]() и
и
![]() -
монотонно возрастающие функции верхнего
предела b.
Монотонно возрастающая функция имеет
конечный предел тогда и только тогда,
когда она ограничена сверху. Пусть
-
монотонно возрастающие функции верхнего
предела b.
Монотонно возрастающая функция имеет
конечный предел тогда и только тогда,
когда она ограничена сверху. Пусть
![]() сходится.
G(b)
ограничена
сходится.
G(b)
ограничена
![]()
![]() ,
F(b)
ограничена, т.е.
,
F(b)
ограничена, т.е.
![]() сходится.
Пусть
сходится.
Пусть
![]() расходится
расходится
![]() F(b)
неограничена
F(b)
неограничена
![]() G(b)
неограничена, т.е.
G(b)
неограничена, т.е.
![]() расходится.
расходится.
Признак сравнения в предельной форме.
Пусть
неотрицательные функции f(x)
и g(x)
интегрируемы по любому отрезку [a,
b]
и пусть существует конечный
![]() .
Тогда несобственные интегралы
.
Тогда несобственные интегралы
![]() и
и
![]() сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
![]() Док-во.
Док-во.
Так
как функции неотрицательны, то K
> 0. По определению предела для
![]() существует
такое значение x0,
что при x
>
x0
выполняется
существует
такое значение x0,
что при x
>
x0
выполняется
![]() .
Дальше рассуждения простые: пусть a1
= min{a,
x0};
если сходится
.
Дальше рассуждения простые: пусть a1
= min{a,
x0};
если сходится
![]() ,
то сходится
,
то сходится
![]() ,
тогда, по теореме сравнения, сходится
,
тогда, по теореме сравнения, сходится
![]()
![]() сходится
сходится
![]()
![]() сходится.
Если расходится
сходится.
Если расходится
![]() ,
то расходится
,
то расходится
![]() ,
тогда, по теореме сравнения, расходится
,
тогда, по теореме сравнения, расходится
![]()
![]() расходится
расходится![]()
![]() расходится.
Случаи, когда сходится или расходится
расходится.
Случаи, когда сходится или расходится
![]() ,
рассмотреть самостоятельно.
,
рассмотреть самостоятельно.
![]() Сравнение
интеграла
Сравнение
интеграла
![]() со
"стандартным" интегралом
со
"стандартным" интегралом
![]() в
предельной форме позволяет сформулировать
такое правило: если при
в
предельной форме позволяет сформулировать
такое правило: если при
![]() неотрицательная
функция f(x)
- бесконечно малая порядка малости выше
первого по сравнению с
неотрицательная
функция f(x)
- бесконечно малая порядка малости выше
первого по сравнению с
![]() ,
то
,
то
![]() сходится;
если f(x)
не является бесконечно малой или имеет
порядок малости единица или ниже, то
интеграл расходится.
сходится;
если f(x)
не является бесконечно малой или имеет
порядок малости единица или ниже, то
интеграл расходится.
10. Несобственные интегралы c особенностями в нескольких точках.
![]() Разобьем инт (а,б) так, чтобы интегралы
на каждом интервале разбиения имели
единств. особенность.
Разобьем инт (а,б) так, чтобы интегралы
на каждом интервале разбиения имели
единств. особенность.
Опр:
Если все несобственные интегралы на
интервале разбиения сходились, то
интеграл ![]() назывался сходящимся.
назывался сходящимся.
Если
хотя бы 1 из интегралов расходится, то
![]() расход.
расход.
![]()
расход сход
Интегральный признак сходимости числовых рядов.
Если
функция ![]() непрерывна и не возрастает на
непрерывна и не возрастает на ![]() то
то ![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Док-во:
 По
теореме о среднем.
По
теореме о среднем.
![]()
![]()
![]()
Если
![]() сходящ., то
сходящ., то ![]() органичен
сверху => сходящ.
органичен
сверху => сходящ.
Если интеграл сход., то и числ. ряд сходится(левое нер-во).
11. Функции многих переменных
Рассмотрим множество E всех упоряд пар чисел (х,у). Если каждой паре приведено в соответств число Z в силу некотор закона то говорят, что на множ-ве Е определена функция Z=f(x,y). График изображается нек поверхностью в 3х мерном прост-ве
Линии уровня Z=f(x,y) это линия f(x,y)=C, C=const на плоскости (х,у)в которой функция сохраняет постоянное значение С.
Понятие окрестности на плоскости
Мн-во т(х,у) : (х-х0)2+(у-у0)2<a2 назыв открытым радиуса а с центром (х0,у0)
Мн-во т(х,у) : |х-х0|<a , |у-у0|<b (a,b>0) назыв открыт прямоугольником
Любой открытй круг радиуса ε>0 или открытый квадрат со стороной 2ε с центром в (х0,у0)
Называется ε-окрестностью т (х0,у0)
Предел последовательности
Пос-ть
{(xk,yk)}->т(х0,у0)
при к->беск, если
![]() ->0
или для любого ε>0 сущn0
принадл N
: для люб k>
n0
т(хk,уk)
нах в ε-окрестности т(х0,у0)
->0
или для любого ε>0 сущn0
принадл N
: для люб k>
n0
т(хk,уk)
нах в ε-окрестности т(х0,у0)
Предел функции
По Коши: lim( x->x0, y->y0) f(x,y)=A если f(x,y) определена в нек окрес-ти т(х0,у0) за исключением быть может самой этой точки. И для любого ε>0 сущ δ>0 :
|f(x,y)-A|<ε
для любых х,у: 0<![]() <δ
<δ
По Гейне: lim( x->x0, y->y0) f(x,y)=A если f(x,y) определена в нек окрес-ти т(х0,у0) за исключением быть может самой этой точки и lim( xк->x0, yк->y0) f(xк,yк)=A
Предел функции по направлению
Пусть
![]() (ωх,ωу):
(ωх,ωу):
![]() ,произвольный
единичный вектор вида (х0+tωx,
y0+tωy),
t>0
образуют луч выходящий из точки (х0,у0)
в направлении
,произвольный
единичный вектор вида (х0+tωx,
y0+tωy),
t>0
образуют луч выходящий из точки (х0,у0)
в направлении![]() .Lim(t->0)
f(х0+tωx,
y0+tωy)
назыв пределом функции f(x,y)
в т(х0,у0)
в направлении
.Lim(t->0)
f(х0+tωx,
y0+tωy)
назыв пределом функции f(x,y)
в т(х0,у0)
в направлении
![]()
Свойства предела функции двух переменных
1 lim( x->x0, y->y0) (f(x,y)+- g(x,y))= lim( x->x0, y->y0) f(x,y) +- lim( x->x0, y->y0) g(x,y)
2 lim( x->x0, y->y0) (f(x,y)* g(x,y))= lim( x->x0, y->y0) f(x,y) * lim( x->x0, y->y0) g(x,y)
3
lim( x->x0, y->y0) (f(x,y)/ g(x,y))= lim( x->x0, y->y0)
f(x,y) / lim( x->x0, y->y0) g(x,y)![]() 0
0
Теорема
о сохранении знака предела.
Если функция f(x,y) имеет предел в точке
(х0,y0) то существует δ>0: для любого х,у:
0<![]() <
δ |f(x,y)|>|A|/2 и функция сохраняет знак
числа А в δ окрестности. Док-во: пусть
ε=|A|/2>0
<
δ |f(x,y)|>|A|/2 и функция сохраняет знак
числа А в δ окрестности. Док-во: пусть
ε=|A|/2>0
Существ δ>0 | f(x,y)-A|<|A|/2
|A|/2>|A- f(x,y)|>=|A|-| f(x,y)|
| f(x,y)|>|A|-|A|/2=|A|/2
f(x,y)>A/2 при A>0
f(x,y)<A/2 при А<0
№12. Непрерывность в точке функции двух переменных
f(x,y) непр в (х0; y0) если она определена в нек окр-ти этой т., в том числе и в самой этой т.
Если lim(x->x0, y->y0) f(x,y)=f(x0, y0)
Замечание: lim(∆x->x0, ∆y->y0) f(x0+∆x, y0+∆y)=f(x0, y0)
Свойства функций непрерывных в точке(1арифметические,2непрерыв сложн функции, 3сохранение знака)
1
f(x,y),
g(x,y)
непр в (x0,
y0),
тогда f+-g,
f*g,
f/g(g
x0,
y0)![]() 0)
непр в (x0,
y0)
0)
непр в (x0,
y0)
2 f(x,y) непр в (x0, y0), x=φ(u,v),y=ψ(u,v) непр в (u0,v0).Тогда f(φ(u,v), ψ(u,v)) непр в (u0,v0)
3
f(x,y) непр
в
(x0, y0), f(x0, y0)
![]() 0.Тогда
f(x,y)
сохр знак числа f(x0,
y0)
в нек окр-ти (x0,
y0).
0.Тогда
f(x,y)
сохр знак числа f(x0,
y0)
в нек окр-ти (x0,
y0).
Опр.Частная производная от фун. f(x,y) по х в точке (х,у).
f(штрих)x=df/dx=lim(h->0)f(x=h,y)-f(x,y)/h
Частная производная от фун. f(x,y) по y в точке (х,у).
f(штрих)x=df/dy=lim(h->0)f(x,y+h)-f(x,y)/h
f(штрих)x(x0,y0)-это тангенс угла наклона к Ох касательной сечения поверхности z=f(x,y)плоскости y=y0 в точке с абсциссой x0.
Опр.Смешаная f’’yx=d^2f/dxdy=d/dy;f’’xy=d^2f/dydx=d/dx
Теорема:Пусть f(x,y) определена вместе со своими частными произв. df/dx,df/dy,d^2f/dxdy,d^2f/dydx в некоторой окрест. точки (х0,у0), причём смешанная произв. 2-ого порядка непрерыв. в точке (х0,у0) тогда d^2(x0,y0)/dxdy=d^2f(x0,y0)/dydx.
Понятие дифференцируемости для функции многих переменных.
Теорема:Если фун. f(x,y,z) имеет непрерыв. частн. произв. в точках (x,y,z) то её приращение в этой точке можно записать в виде f=df/dxx+df/dyy+df/dzz+0(ρ); ρ=(x2+y2).
Теорема:(Необх и дост усл.)Для того чтобы фун. f была дифф. в точке необх. чтобы она имела в этой точке частн. произв. и дост. чтобы она имела в этой точке непрер. частн произв.
Следств:Если фун. дифф. в точке, то она непрер в этой точке.
Дифференциал:Главная линейная часть приращения диффер. фун. f(x,y,z) назыв. дифференциалом этой точке соотв. приращ. независимых переменных и обозначенных df=df/dx x+df/dyy+df/dzz(для f(x,y,z)).
№14.Дифференцирование сложной функции.Теорема:Пусть фун. u=f(x,y,z) диффер. в (x,y,z) некоторого мн-ва фун. x=x(f),y=y(f),z=z(f) имеет произв. в точке f.du/dt=df/dx*dx/dt+df/dy*dy/dt+dt/dz*dz/dt.
Теорема:Фун. u=f(x,y,z)диффер. в т. (x,y,z,),x=x(t,z),y=y(t,z)z=(t,z).Тогда du/dz=df/dx*dx/dt+df/dy*dy/dt+dt/dz*dz/dt.
Билет 15. Производная по направлению. Градиент.
Теорема:
Если f(x,y,z) дифференцируема в т.(x,y,z), то производная функции по направлению единичного вектора n(cos α, cos β, cos γ):
∂f/∂n=∂f/∂x * cos α + ∂f/∂y * cos β + ∂f/∂z * cos γ; где α, β, γ – углы между n и положительным направлением Ox, Oy, Oz.
Доказательство:
По определению производной по направлению:
∂f/∂n = lim((f(x-tcosα, y+tcosβ, z+tcosγ)-f(x,y,z))/t) = d/dt f(x+tcosα, y+tcosβ, z+tcosγ)|0 =
= ∂f/∂x * cosα + ∂f/∂y * cosβ + ∂f/∂z * cosγ (по формуле производной сложной функции)
Градиентом функции f(x,y,z) в т. М(x,y,z) называется вектор с началом в т. М и координатами ∂f(M)/∂x, ∂f(M)/ ∂y, ∂f(M)/ ∂z.
gradf = ∂f(M)/∂x * i + ∂f(M)/ ∂y * j + ∂f(M)/ ∂z * k. (i,j,k - векторы)
Производная по направлению n:
∂f/∂n = (gradf, n) - скалярное произведение.
∂f/∂n – проекция вектора gradf на вектор n, то есть ∂f/∂n ≤ |gradf|
Градиент указывает направление наискорейшего роста функции в данной точке.
№16. Дифференциалы высших порядков. Формула Тейлора для функции многих переменных.
z = f(x,y)
dz = (∂z/∂x)dx + (∂z/∂y)dy – дифференциал 1-го порядка.
Диф-циал 2-го порядка – диф-циал функции от 1-го диф-циала:
d2z = d(dz)
Аналогично для 3-го порядка и так далее (d3z = d(d2z), …)
Если функция имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
d2z = (∂2z/∂x2)dx2 + 2(∂2z/∂x∂y)dxdy + (∂2z/∂y2)dy2
d3z = (∂3z/∂x3)dx3 + 3(∂3z/∂x2∂y)dx2dy + 3(∂3z/∂x∂y2)dxdy2 + (∂3z/∂y3)dy3
dnz = ((∂/∂x)dx + (∂/∂y)dy)nz
Формула Тейлора:
Пусть функция f(x.y) имеет все частные производные до n-го порядка в окрестности т. Р(x0,y0)
Точка Р1(x0 + ∆x, y0 +∆y) лежит в окрестности т. Р. Соединим т. Р и Р1 отрезком:
x = x0 + t∆x 0 ≤ t ≤ 1
y = y0 + t∆y - это типа система
F(t) = f(x0 + t∆x, y0 + ∆y)
Рассм
ф-цию F(t)=f((x0+Δx,y0+Δy).
Ф-ла Маклорена для F(t):
F(t)=F(0)+(F’(0)t)/1!+(F”(0)t2)/2!+…+(F(n-1)(0)tn-1)/(n-1)!+(Fn(θ)tn)/n!,
0<θ<t
F’(t)=![]()
При t=0
F’(0)=dF(P);
F”(0)=d2F(P)
и тд. Итак ф-ла Тейлора для ф-ции 2ух
перемен: Δf(P)=df(P)/1!+d2f(P)/2!+…+1/n!*dnf(x0+θΔx,y0+θΔy).
При t=0
F’(0)=dF(P);
F”(0)=d2F(P)
и тд. Итак ф-ла Тейлора для ф-ции 2ух
перемен: Δf(P)=df(P)/1!+d2f(P)/2!+…+1/n!*dnf(x0+θΔx,y0+θΔy).
