Движение по прямой с постоянным ускорением Примеры решения задач

1.Тело движется с постоянным ускорением и нулевой начальной скоростью. Показать графически, что пути, проходимые телом за последовательные равные промежутки времени, относятся как последовательные нечетные числа.

Решение. При равноускоренном движении тела с нулевой начальной скоростью его скорость с течением времениtизменяется по закону

v = at,

где a- ускорение.

Построим график скорости (см. рис.) и отметим на оси tравные промежуткиОА₁=А₁А₂=А₂А₃=А₃А₄= …; из точекА₁,А₂, … проведем пунктиром вертикальные прямые до пересечения с графиком скорости в точкахВ₁,В₂,В₃, … . Тогда путь, пройденный за первый промежуток, численно равен площади треугольникаОА₁В₁; пути, пройденные за последующие промежутки, равны площадям соответствующих трапеций. Из графика видно, что площадь первой трапецииА₁А₂В₂В₁составляет три площади треугольникаОА₁В₁; площадь следующей трапецииА₂А₃В₃В₂равна пяти площадям треугольникаОА₁В₁и т.д. Следовательно, отношение путей, проходимых телом за последовательные равные промежутки времени равно:

S₁:S₂:S₃: …: S_n = 1:3:5: …: (2n – 1).

2.За пятую секунду равноускоренного движения с нулевой начальной скоростью тело проходит путьS₂= 36 м. Какой путьS₁проходит тело за первую секунду этого движения?

Решение.Из решения предыдущей задачи следует, что

S₁:S₅= 1:9.

Следовательно,

4 м.

3. Свободно падающее тело за последнюю секунду падения прошло 1/3 своего пути. Найти время падения t и высоту h, с которой упало тело.

Решение.Из законов движения тела с постоянным ускорением и нулевой начальной скоростью получим следующие уравнения:

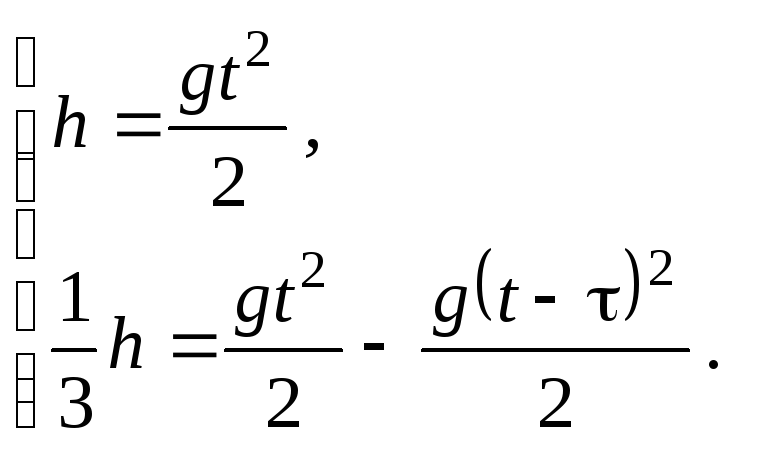
Здесь = 1 с. Решая полученную систему уравнений, найдем:

По условию задачи t> 1. Этому условию удовлетворяет корень5,4 с. Далее получим:

м.

4.Воздушный шар поднимается с поверхности Земли вертикально вверх с ускорениемa = 2 м/с². Через= 10 с после начала движения от корзины шара оторвался предмет. На какую максимальную высотуh_mподнимется этот предмет? Через какое времяt₁и с какой скоростью v₁он упадет на Землю?

Решение.Предмет оторвался от корзины воздушного шара на высотеимея скорость v₀=а, направленную вертикально вверх. Выберем систему отсчета - осьОХ, направленную вертикально вверх, и изобразим на рисунке положение предмета в момент отрыва от корзины. Максимальная высота равна

h_m=h₀+S_m,

где - путь, пройденный предметом за время после отрыва до подъема на максимальную высоту, т.е.

120 м.

Далее очевидно, что после отрыва предмет движется вверх в течение времени до остановки в наивысшей точке, после чего он свободно падает с высотыh_m; при этом время его паденияtнайдем из соотношеният.е.

Следовательно,

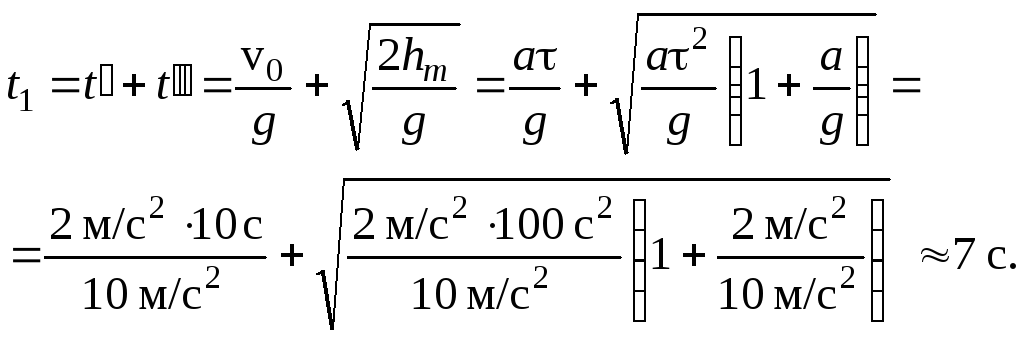
Скорость предмета, упавшего на Землю, определим из соотношения

т.е.

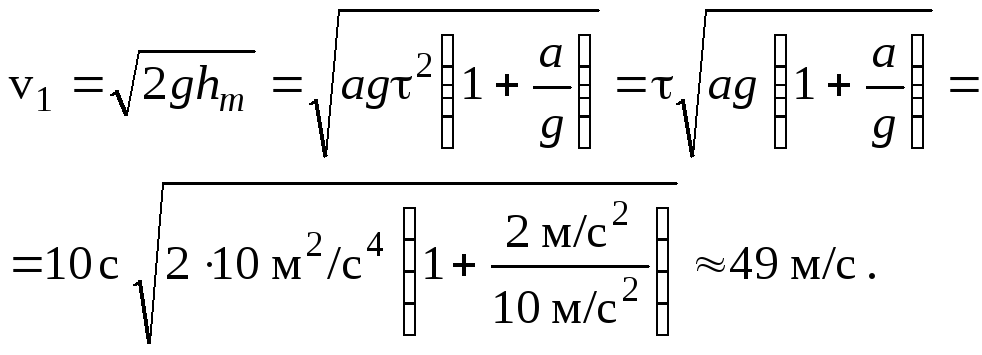
5.С каким промежутком времени оторвались от карниза крыши две капли воды, если спустя две секунды после начала падения второй капли расстояние между ними былоS= 25 м?

Решение. Пусть  - промежуток времени между отрывом первой и второй капель, t = 2 с - время с момента отрыва второй капли. Тогда к моменту отрыва второй капли первая капля прошла путь S₀ = g²/2 и имела скорость v₀ = g. Далее очевидно, что расстояние между каплями равно

где - путь, пройденный первой каплей за времяt,- путь, пройденный второй каплей за это же время.

Следовательно,

Решая полученное уравнение и учтя, что > 0, найдем:

6.По наклонной доске пустили катиться снизу вверх шарик. На расстоянииl= 30 см от начала броска шарик побывал дважды: черезt₁= 1 с и черезt₂= 2 с после начала движения. Определить начальную скорость v₀и ускорениеaшарика, считая его постоянным.

Решение.Запишем закон движения шарика, выбрав осьOX, направленную вдоль движения шарика:

Перепишем это уравнение так:

При x=lэто уравнение имеет корниt₁иt₂.

Поэтому по теореме Виетта

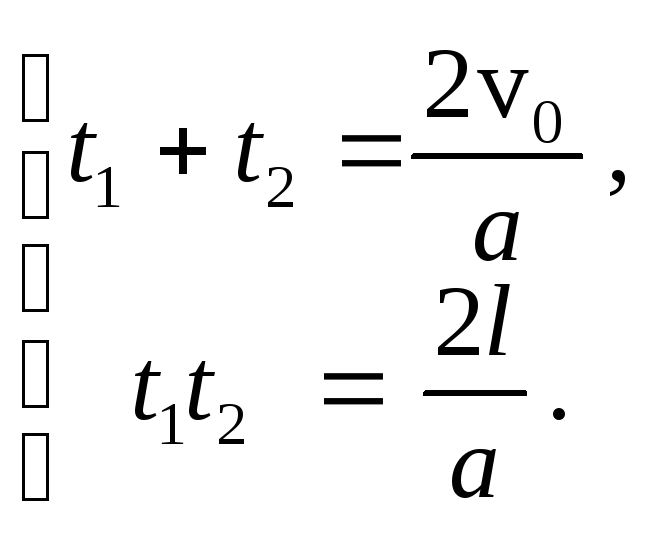
Решая эту систему, найдем:

= 30 см/с²,

= 45 см/с.

Замечание. Данную задачу можно решить иначе, а именно: воспользовавшись законом движениязаписать два уравненияx(t₁) =lиx(t₂) =l, а затем решать полученную систему уравнений с двумя неизвестными v₀иa.