
- •I. Механика
- •1. Кинематика Основные понятия и определения
- •Перемещение, путь, средняя скорость Примеры решения задач
- •Задачи и упражнения
- •Контрольные вопросы
- •Равномерное прямолинейное движение Примеры решения задач
- •Задачи и упражнения
- •Движение по прямой с постоянным ускорением Примеры решения задач
- •Задачи и упражнения
- •Свободное движение тел, брошенных под углом к горизонту Примеры решения задач
- •Задачи и упражнения
- •Относительность движения Примеры решения задач
- •Задачи и упражнения
- •Ускорение при криволинейном движении. Кинематика вращательного движения Примеры решения задач
- •Задачи и упражнения
- •Контрольные вопросы
Перемещение, путь, средняя скорость Примеры решения задач
1.Материальная точка прошла
половину окружности. Найти отношение
средней путевой скорости <v> к модулю
средней векторной скорости![]() .
.
Решение. Из определения средних значений путевой и векторной скоростей с учетом того, что путь, пройденный материальной точкой за время движенияt, равенR, а величина перемещения 2R, гдеR- радиус окружности, получим:
![]()


2.Автомобиль проехал первую треть пути со скоростью v1= 30 км/ч, а оставшуюся часть пути - со скоростью v2= 40 км/ч. Найти среднюю скорость <v> на всем пройденном пути.
Решение. По определению <v> =![]() гдеS- путь, пройденный за времяt.
Очевидно, что
гдеS- путь, пройденный за времяt.
Очевидно, что![]() Поэтому искомая средняя скорость равна
Поэтому искомая средняя скорость равна
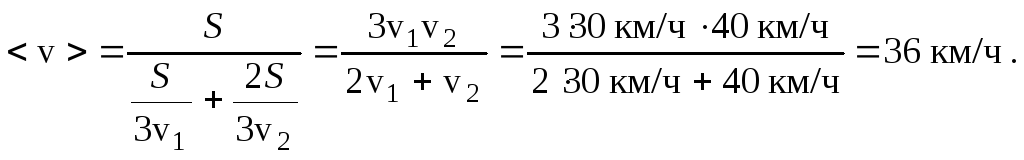
3.Студент проехал половину пути на велосипеде со скоростьюv1= 12 км/ч. Далее половину оставшегося времени он ехал со скоростьюv2= 10 км/ч, а оставшуюся часть пути шел пешком со скоростьюv3= 6 км/ч. Определить среднюю скорость движения студента <v> на всем пути.
Решение. По определению![]() гдеS –путь, аt- время движения.
Ясно, чтоt=t1+t2+t3.
Здесь
гдеS –путь, аt- время движения.
Ясно, чтоt=t1+t2+t3.
Здесь![]() -
время движения на первой половине пути,t2– время движения на втором
участке пути иt3- на третьем.
По условию задачиt2=t3.
Кроме того,S/2 =v2t2+ v3t3= (v2+v3)t2.
Отсюда следует:
-
время движения на первой половине пути,t2– время движения на втором
участке пути иt3- на третьем.
По условию задачиt2=t3.
Кроме того,S/2 =v2t2+ v3t3= (v2+v3)t2.
Отсюда следует:
![]()
Подставив t1 и t2+t3 = 2t2 в выражение для средней скорости, получим:

4.Расстояние между двумя станциями поезд прошел за времяt1= 30 мин. Разгон и торможение длилисьt2= 8 мин, а остальное время поезд двигался равномерно со скоростью v = 90 км/ч. Определить среднюю скорость поезда <v>, считая, что при разгоне скорость увеличивалась с течением времени по линейному закону, а при торможении уменьшалась тоже по линейному закону.
Р

![]()
Задачи и упражнения
1.1.Мяч упал с высотыh1 = 4 м,
отскочил от пола и был пойман на
высотеh2= 1 м. Чему равен путьSи величина перемещения![]() ?
?
1.2.Материальная точка переместилась на плоскости из точки с координатамиx1= 1 см иy1= 4cм в точку с координатамиx2= 5 см иy2= 1 см. Построить вектор перемещения и с помощью линейки определить модуль вектора перемещения и проекции вектора перемещения на осиxиy. Найти эти же величины аналитически и сравнить результаты.
1.3.Первую половину пути поезд шел со скоростью вn= 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути <v> = 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути ?
1.4.Первую половину времени своего движения велосипедист проехал со скоростью v1= 18 км/ч, а вторую половину времени - со скоростью v2= 12 км/ч. Определить среднюю скорость движения велосипедиста.
1.5. Движение двух автомобилей
описывается уравнениями![]() и
и![]() ,
где все величины измеряются в системе
СИ. Запишите закон изменения расстояния
,
где все величины измеряются в системе
СИ. Запишите закон изменения расстояния![]() между автомобилями от времени и найдите
между автомобилями от времени и найдите![]() через время
через время![]() с.
после начала движения.
с.
после начала движения.
