
- •Матанализ Конспект лекций
- •Лекция №1 Тема: Введение
- •Окрестности.
- •Модуль и основные неравенства.
- •Функция. Монотонность. Ограниченность.
- •Монотонные последовательности
- •Лекция №3 Тема: Последовательности Бесконечно малые последовательности
- •Свойства бесконечно малой последовательности.
- •Теоремы о пределах числовых последовательностей.
- •Лекция №4 Тема: Бесконечно большие последовательности .
- •Бесконечно большие последовательности.
- •Связь между бесконечно большими и бесконечно малыми величинами.
- •Основные теоремы о существование предела последовательности.
- •Лекция №6 Тема: Замечательные пределы Теорема
- •Первый замечательные пределы.
- •Односторонние пределы. Определение
- •Определение
- •Второй замечательный предел.
- •Лекция №7 Тема: Сравнение бесконечно больших и бесконечно малых.
- •Шкала бесконечности.
- •Показательные бесконечности.
- •Логарифмическая бесконечность
- •Основные эквивалентности.
- •Лекция №8 Тема: «Асимптотические формулы»
- •Непрерывность некоторых функций.
- •Лекция №9 Тема: «Точки разрыва»
- •Классификация точек разрыва функции.
- •Основные теоремы о непрерывных функциях.
- •Теоремы Вейштрасса.
- •Лекция №10 Тема: «Коши, производные»
- •Разность значений функций.
- •Обозначения:
- •Физический смысл производной.
- •Геометрический смысл производной.
- •Основные теоремы о производной.
- •Лекция №11 Тема: «Производные, дифференциал»
- •Дифференциал функции.
- •Гиперболические функции.
- •Лекция №12 Тема: «Линеаризация» Геометрический смысл дифференциала функции и уравнение касательной.
- •Линеаризация функции.
- •Приближенные вычисления и оценка погрешности вычисления.
- •Погрешности вычисления.
- •Изучение поведения функции при помощи первой производной.
- •Экстремумы функции.
- •Лекция №13 Тема: «Экстремумы»
- •Производная функции высшего порядка.
- •Лекция №14 Тема: Производная функции высшего порядка.
- •Правила Лопиталя.
- •Формулы Тейлора.
- •Свойства многочлена Тейлора.
- •Формула Тейлора с остаточным членом пеано.
- •Лекция №15 Тема: Пять основных разложений
- •Формула Тейлора с остаточным членом в форме Лангранджа.
- •Лекция №17 Тема: Асимптоты. Полное исследование функции. Асимптоты.
- •Необходимые и достаточные условия существования наклонной асимптоты.
- •Полное исследование функции.
- •Лекция №18
- •Оценка скорости сходимости.
- •Формула Тейлора с остаточным членом в форме Лангранджа в точке xn
- •Вектор функция. Параметрическая производная.
Лекция №17 Тема: Асимптоты. Полное исследование функции. Асимптоты.
Вертикальные
Пусть функция f(x) определена в
 ,
тогда прямая х=х0называется
правой вертикальной асимптотой для
функцииf(x)
,
тогда прямая х=х0называется
правой вертикальной асимптотой для
функцииf(x)
 Пусть
функцияf(x)
определена в
Пусть
функцияf(x)
определена в ,
тогда прямая х=х0называется
левой вертикальной асимптотой для
функцииf(x)
,
тогда прямая х=х0называется
левой вертикальной асимптотой для
функцииf(x)

Наклонные асимптоты
2.1 Пусть функция f(x)
определена в![]() ,
тогда прямаяy=kx+bназывается правой наклонной асимптотой
для функцииf(x).
(Еслиk=0, то говорят, чтоy=b–
горизонтальная асимптота).
,
тогда прямаяy=kx+bназывается правой наклонной асимптотой
для функцииf(x).
(Еслиk=0, то говорят, чтоy=b–
горизонтальная асимптота).

2.2 Пусть функция f(x)
определена в![]() ,
тогда прямаяy=kx+bназывается левой наклонной асимптотой
для функцииf(x).
,
тогда прямаяy=kx+bназывается левой наклонной асимптотой
для функцииf(x).


Необходимые и достаточные условия существования наклонной асимптоты.
Пусть функция f(x) определена в О(+) и
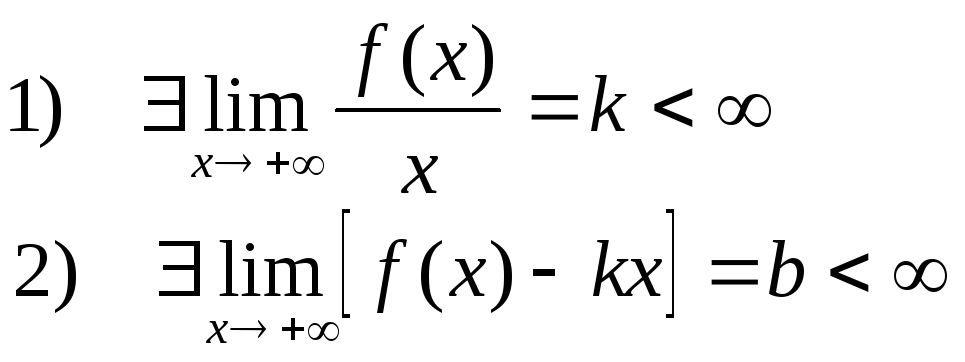
тогда прямая y=kx+b правая наклонная асимптота
![]()
Замечание: если условие 1) не выполнено, то нужно посчитать пределlim(f(x)), чтобы выяснить поведение
х+
функции на бесконечности.
Полное исследование функции.
Область определения
Симметрия и периодичность
Вертикальные асимптоты
Наклонные асимптоты
Критические точки, если есть, то находим точки экстремума и промежутки возрастания и убывания функции f'(x)=0 или f’(x) не существует, аf(x) существует
Возможные точки перегиба f’’(x)=0, либоf’’(x) не существует, ноf’(x) существует следовательно промежутки выпуклости и вогнутости
Точки пересечения с осями координат и промежутки знака постоянства (если можно)
Пример:
![]()
Область определения D:x¹3
Функция не симметрична и не периодична

![]()
Þх=3 правая и левая вертикальная асимптота
4)

Þy=0 правая и левая горизонтальная асимптота
5)![]()
критическая точка х1=-3/2

f(-3/2)=4/243
6)![]()
критическая точка х2=-3

f(-3)=1/72
7)x=0 y=0

Приближенные методы решения уравнения f(x)=0
1) Метод хорд
а) f(x),f’(x),f’’(x) – непрерывны на отрезке [a,b]
б) f(a)f(b)<0
в) f’(x) иf’’(x) – сохраняют знаки на отрезке [a,b]
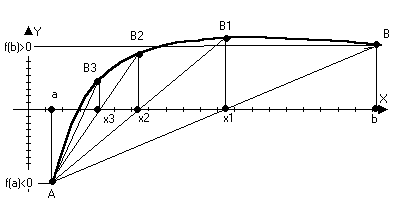
f()=0;A(a;(f(a)),B(b;f(b))

Лекция №18

Оценка скорости сходимости.
 2
2
2) Метод касательных (метод Ньютона)
f(x)=0
1)f(x),f’(x),f’’(x)-непрерывна на [a,b]
2)f(a), f(b) <0
3)f’(x),f’’(x) – сохраняет знак на [a,b]


точка пересечения х1 – это точка пересечения касательной с осью Ох
Yкас=0, x=x1
0=f(b)+f’(b)(x1-b)
f’(b)b-f(b)=f’(b)x1

Формула Тейлора с остаточным членом в форме Лангранджа в точке xn

c – лежит между х и хn
Положим x=; f()=0

M>0:|f”(x)|M
x[a,b] m>0:|f’(x)|m;x[a,b]

Надо выбирать отрезок так b-a<1
|f”(x)|M
Вектор функция. Параметрическая производная.
![]()

![]()
По закону (1) ставиться в соответствие вектор r(t). (x(t),y(t) – заданные числовые функции
r(t) – вектор функция. Кривая описываемая концом вектора – называется годографом.

|
t |
0 |
1 |
-1 |
2 |
3 |
½ |
|
x(t) |
0 |
1 |
-1 |
2 |
3 |
½ |
|
y(t) |
0 |
0 |
-2 |
-2 |
-6 |
1/4 |
|
r(t) |
0 |
i |
-i-2j |
2i-2j |
3j-6j |
1/2i+1/4j |


Видим, что кривые на плоскости можно задать в виде:

 Называется
параметрическое задание кривой, где t
–параметр
Называется
параметрическое задание кривой, где t
–параметр
x2+y2=r2


Остроида
x2/3+y2/3=a2/3


Циклоида


1На концах отрезка [a,b] и на концах принимает значение разных знаков
2(x-x0)-бесконечно малое при хх0
1x0
1(∆x) – бесконечно малое при∆х0, а(∆x)∆х – есть о∆х
1Y– ордината касательной
a–x-x0=∆x
1∆-погрешность вычисления.
Теорема–Еслиf(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), тос(a,b): f(b)-f(a)=f(c)(b-a)
1(x-x0)=∆x
1Теорема– Еслиf(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), тос(a,b): f(b)-f(a)=f(c)(b-a)
II–g’(c1)=0 по условия теоремы
III– (b-a)=0
4- Теорема (Ролля): Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда с(a,b): f(c)=0
10((x-x0)n)(x-x0) – остаточный член в форме пеано
ii(х-х0) – бесконечно малое при хх0
* o’1 x2n+2=xx2n+1=o(x2n+1)
#![]() -
остаточный член в форме Лангранджа
-
остаточный член в форме Лангранджа
$-Tn(x) – многочлен Тейлора
Rn(x)-остаточный член в форме Лангранджа
