
- •Московский государственный институт
- •Теоретические сведения Общие сведения о цифровых (дискретных) фильтрах
- •Цифровые фильтры с конечной импульсной характеристикой (ких). Импульсная характеристика нерекурсивного (трансверсального) фильтра
- •Комплексная частотная характеристика нрцф и ее связь с их
- •Основные свойства комплексной частотной характеристики цифрового фильтра
- •Применение нрцф в качестве согласованных фильтров
- •Инструкция по работе с эвм
- •Impz(b,a); %построение простой (невзвешенной) их
- •Impz(b,a); %построение их
- •Impz(b,a); %построение их
- •Impz(b,a); %построение импульсной характеристики
- •Xlim([0 30]) %пределы по горизонтальной оси
- •Задание на выполнение работы
- •Исследование частотных характеристик фильтров
- •Проектирование нрцф методом частотной выборки
- •Расчет и исследование работы согласованного нрцф
- •Требования к отчету
- •Контрольные вопросы
- •Литература
Московский государственный институт
ЭЛЕКТРОННОЙ ТЕХНИКИ (ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)




Д.В.Незлин, В.П.Бец
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ЛАБОРАТОРНОЙ РАБОТЕ №1 “НЕРЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ”
по курсу: "ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ"
Москва 2008
НЕРЕКУРСИВНЫЕ ЦИФРОВЫЕ ФИЛЬТРЫ
Цель работы: изучить принцип построения и характеристики нерекурсивных цифровых фильтров (НРЦФ), исследовать зависимость частотной характеристики фильтра от импульсной характеристики, ознакомиться с алгоритмом расчета нерекурсивного фильтра методом частотной выборки; рассчитать согласованный НРЦФ по параметрам сигнала, ознакомиться с его свойствами.
Продолжительность работы - 4 ч.
Обеспечение занятия: персональный компьютер с матричной системой компьютерной математики Matlab 7.0, программное обеспечение лабораторной работы в папке methodic/МРТУС/ЦОС/201X/Лабораторные работы/Lab 1.
Теоретические сведения Общие сведения о цифровых (дискретных) фильтрах
В цифровых
(дискретных) фильтрах производится
обработка сигналов, преобразованных в
последовательность чисел. Выходную
последовательность
![]() можно выразить через входную
можно выразить через входную![]() и импульсную характеристику (ИХ) фильтра
и импульсную характеристику (ИХ) фильтра
![]() с помощью дискретной свертки
с помощью дискретной свертки
![]() (1)
(1)
В формуле (1)
![]() - интервал
временной дискретизации сигнала,
подлежащего фильтрации, или (что то же
самое) период импульсов, тактирующих
цифровой фильтр;
- интервал
временной дискретизации сигнала,
подлежащего фильтрации, или (что то же
самое) период импульсов, тактирующих
цифровой фильтр;![]() и
и![]() - целые числа. Часто запись в (1) упрощают,
опуская постоянную величину Т:
- целые числа. Часто запись в (1) упрощают,
опуская постоянную величину Т:
![]() (2)
(2)
Как следует из формул (1) и (2), для реализации цифрового фильтра необходимо и достаточно выполнять три операции:
задержку (запоминание) входных чисел на отрезки времени, кратные Т;
умножение этих чисел на значения импульсной характеристики, которые хранятся в ППЗУ;
суммирование полученных произведений.
Различают цифровые фильтры с конечной импульсной характеристикой (КИХ-фильтры) и с бесконечной импульсной характеристикой (БИХ-фильтры).
В первом случае h(nT) принимает ненулевые значения на ограниченном интервале времени, за пределами которого h(nT) = 0. Во втором случае длительность импульсной характеристики не ограничена.
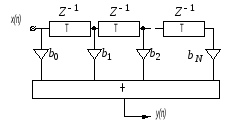
Цифровые фильтры с конечной импульсной характеристикой (ких). Импульсная характеристика нерекурсивного (трансверсального) фильтра
КИХ-фильтры обычно
реализуют с помощью нерекурсивных
(трансверсальных) фильтров, в которых
отсутствует обратная связь. Структурная
схема такого фильтра представлена на
рис.1. Здесь символом
![]() обозначен элемент задержки сигнала на
величинуТ,
маленьким треугольником – операцию
умножения на стоящее рядом с ним число.
Множители
обозначен элемент задержки сигнала на
величинуТ,
маленьким треугольником – операцию
умножения на стоящее рядом с ним число.
Множители
![]() называют коэффициентами фильтра. Число
элементов задержкиN
называется порядком фильтра.
называют коэффициентами фильтра. Число
элементов задержкиN
называется порядком фильтра.
Рис.1. Блок-схема
КИХ-фильтра
![]() подать на вход нерекурсивного фильтра
единичный дискретный импульс, то выходная
последовательность (являющаяся ИХ)
будет иметь вид
подать на вход нерекурсивного фильтра
единичный дискретный импульс, то выходная
последовательность (являющаяся ИХ)
будет иметь вид![]() .
Значит, между значениями ИХ и коэффициентами
нерекурсивного фильтра существует
простая связь:
.
Значит, между значениями ИХ и коэффициентами
нерекурсивного фильтра существует
простая связь:![]()
Число отсчетов ИХ
равно N,
а ее длительность, очевидно, составляет![]() .
Таким образом, заданиеh(n)
непосредственно определяет структуру
такого фильтра.
.
Таким образом, заданиеh(n)
непосредственно определяет структуру
такого фильтра.
Комплексная частотная характеристика нрцф и ее связь с их
Комплексная частотная характеристика НРЦФ связана с ИХ парой преобразований Фурье:
![]() ;
(3)
;
(3)
![]() (4)
(4)
В формулах (3) и (4)
![]() -
нормированная частота, измеряемая в
радианах или градусах;
-
нормированная частота, измеряемая в
радианах или градусах;![]() ,
где
,
где![]() - круговая частота, рад/с.
- круговая частота, рад/с.
Если
![]() приближенно представлена дискретными
выборками вN
равноотстоящих точках на интервале
приближенно представлена дискретными
выборками вN
равноотстоящих точках на интервале
![]() (или
(или![]() ),
то
),
то![]() определяется не интегральным
преобразованием (4), а дискретным
преобразованием Фурье:
определяется не интегральным
преобразованием (4), а дискретным
преобразованием Фурье:
![]() .
(5)
.
(5)
При этом точный вид частотной характеристики фильтра, заданного ИХ (5), по-прежнему определяется формулой (3).
Если ИХ фильтра
симметрична или антисимметрична
относительно ее середины (т.е. точки с
абсциссой
![]() ),
то фазочастотная характеристика фильтра
),
то фазочастотная характеристика фильтра![]() является линейной функцией частоты, во
всяком случае, в пределах полосы
пропускания. Иногда это свойство
нерекурсивного фильтра является весьма
полезным.
является линейной функцией частоты, во
всяком случае, в пределах полосы
пропускания. Иногда это свойство
нерекурсивного фильтра является весьма
полезным.
