Практикум 2.3. Числовые ряды Краткие теоретические сведения и практические упражнения

1. Числовой ряд. Сходящиеся и расходящиеся ряды. Сумма ряда.

Пусть задана бесконечная последовательность чисел Рассмотрим выражение, представляющее собой «сумму бесконечного множества слагаемых». Оно называетсячисловым рядом, а сами числа -членами ряда. Член ряда с произвольным номеромназываетсяобщим членом.

Например, есть ряд с общим членом, аесть ряд с общим членом.

Числа , , и т.д. называются частичными суммами ряда. Обобщая: -я частичная суммаесть сумма первыхчленов ряда: .

В качестве примера рассмотрим ряд .. Члены этого ряда,, образуют геометрическую прогрессию с первым членоми знаменателеми, значит,-я частичная суммаэтого ряда является суммой первыхчленов геометрической прогрессии и может быть найдена по формуле. Таким образом,.

Если последовательность частичных сумм ряда имеет конечный предел, т.е. существует число, то ряд называется сходящимся, а числоназывается суммой ряда. В этом случае также говорят, чторяд сходится к сумме и пишут. Если же равен бесконечности или не существует, то говорят, что рядрасходится или, что он не имеет суммы.

Продолжим рассмотрение примера. Для ряда конечный предел частичных сумм существует: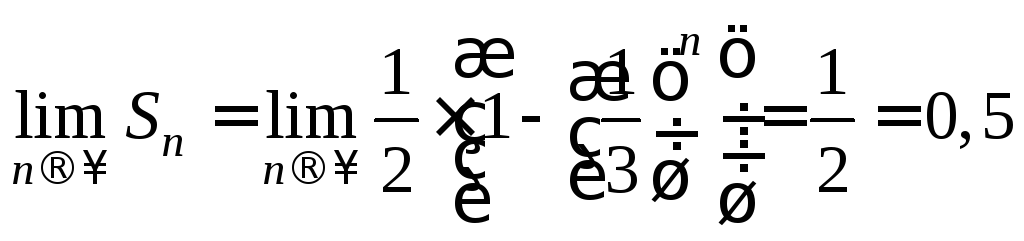. Следовательно, этот ряд сходится и его сумма равна.

Упражнение 1. Создать M-функцию, которая строит в одной системе координат график последовательности членов ряда и график последовательности частичных сумм ряда. При построении этой пары графиков использовать разные цвета и маркеры. В качестве входных параметров M-функции использовать формулу общего члена последовательности и числорассматриваемых членов. В качестве выходных параметров вывести значения. Применить созданную М-функцию для исследования следующих рядов:

1) ; 2); 3).

Опираясь на построенные графики, для каждого ряда выдвинуть гипотезу о сходимости или расходимости ряда. В случае предположения о сходимости ряда указать приблизительное значение суммы ряда.

2. Необходимый признак сходимости.

В приложениях обычно применяются сходящиеся ряды. Поэтому важно знать признаки, по которым можно было бы судить, сходится данный ряд или нет.

Попробуйте установить связь между поведением общего члена ряда на бесконечности и сходимостью ряда, опираясь на результаты выполнения упр. 1.

Подтверждают или опровергают ряды, рассмотренные в упр. 1, следующие гипотезы:

а) Если ряд сходится, то последовательность его членов стремится к нулю при .

б) Если последовательность членов ряда стремится к нулю при , то ряд сходится?

Подтверждение Ваших предположений найдете на следующей странице.

Необходимый признак сходимости. Если ряд сходится, то его -й член стремится к нулю при. Действительно, пусть ряд сходится, т.е. последовательность его конечных сумм имеет конечный предел при. Тогда для этой последовательности выполняется условие Коши: С учетом равенства , последнее выражение является определением того, что последовательностьстремится к нулю при.

Подчеркнем, что мы установили лишь необходимый признак сходимости, т.е. такой, при нарушении которого ряд не может сходиться. С помощью этого признака можно доказывать лишь расходимость ряда.

Упражнение 2. Установить, расходимость каких из следующих рядов можно доказать, используя необходимый признак сходимости (по Вашему желанию: «вручную» или используя MATLAB):

а) ; б).

Упражнение 3. Приведите два примера расходящихся числовых рядов (отличные от рассмотренных в упр. 3), общий член которых стремится к нулю. Используя M-функцию из упр. 1, проиллюстрируйте примеры графически.

Сделав упр. 3, Вы проиллюстрировали, что стремления общего члена ряда к нулю недостаточно для сходимости ряда.