
Лабораторная работа 5
Свободные колебания в колебательном контуре
Цель работы. Изучение затухающих колебаний в колебательном контуре при различных значениях емкости, индуктивности, активного сопротивления.
Приборы и оборудование.Катушка с обмоткой возбуждения и электронным ключом, набор конденсаторов, магазин сопротивлений, генератор прямоугольных импульсов, электронный осциллограф.
Теоретическая часть
На
рис.1. изображена цепь, называемая
последовательным колебательным контуром
(С
- емкость конденсатора, L - индуктивность
катушки, R
- суммарное активное сопротивление
контура). В этой цепи могут возникать
электрические колебания – циклические
изменения протекающего в контуре тока
i
и падений напряжения на элементах цепи.
При
![]() эти колебания являются гармоническими
и запасенная в контуре энергия
эти колебания являются гармоническими
и запасенная в контуре энергия
![]() (1)
(1)
остается постоянной (u – напряжение на конденсаторе). В процессе колебаний происходит лишь перераспределение этой энергии между электрическим полем конденсатора и магнитным полем катушки индуктивности.
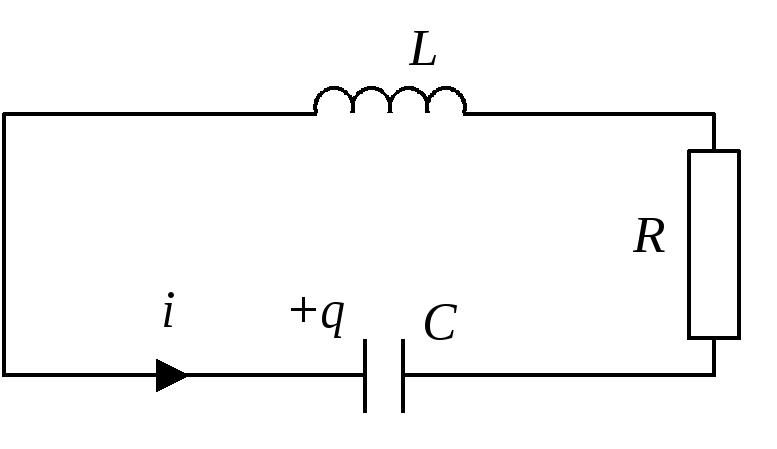
Рис. 1. Последовательный колебательный контур
Если же сопротивление контура R отлично от нуля, то запасенная в контуре энергия W уменьшается во времени вследствие выделения тепла на сопротивлении R:
![]() (2)
(2)
Одно из направлений
тока примем за положительное (оно
обозначено на рис.1 стрелкой). Обозначим
через
![]() заряд той из обкладок конденсатора,
направление от которой к другой обкладке
совпадает с положительным направлением
тока. Из определений силы тока и
электроемкости следует
заряд той из обкладок конденсатора,
направление от которой к другой обкладке
совпадает с положительным направлением
тока. Из определений силы тока и
электроемкости следует
![]() ,
,
![]() ,
(3)
,
(3)
После несложных преобразований из (1) – (3) получим следующее уравнение относительно неизвестной функции времени u=u(t):
![]() ,
(4)
,
(4)
где
![]() ,
,
![]() (5)
(5)
При
![]() уравнение (4) имеет решение
уравнение (4) имеет решение
![]() ,
(6)
,
(6)
описывающее затухающие колебания напряжения (см. рис. 2а). Частота затухающих колебаний
![]() (7)
(7)
зависит
от параметров контура (L,
C
и
R),
а постоянные
![]() и
и![]() определяются начальными условиями
(значениями напряженияu
и тока i
при t = 0).
Множитель
определяются начальными условиями
(значениями напряженияu
и тока i
при t = 0).
Множитель
![]() ,
(8)
,
(8)
стоящий
перед периодической функцией в формуле
(6), называется амплитудой затухающих
колебаний. Она экспоненциально убывает
во времени, причем время, за которое
амплитуда уменьшается в e
раз, равно
![]() .
Величина
.
Величина![]() ,
таким образом, характеризует скорость
затухания амплитуды колебаний и
называется коэффициентом затухания.
,
таким образом, характеризует скорость
затухания амплитуды колебаний и
называется коэффициентом затухания.

Рис. 2. Затухающие колебания напряжения на конденсаторе (а) и тока (б) в колебательном контуре
За
каждый период колебаний
![]() амплитудаUm
убывает в
амплитудаUm
убывает в
![]()
раз. Логарифм этого отношения
![]() (9)
(9)
называется логарифмическим декрементом затухания.
Затухание
колебаний в контуре характеризуют также
добротностью контура
![]() ,
которая определяет относительные потери
энергии за один период колебаний:
,
которая определяет относительные потери
энергии за один период колебаний:
![]() .
(10)
.
(10)
При малом затухании, когда
![]() (11)
(11)
и
![]() (12)
(12)
из формулы (10) после ряда преобразований следует
![]() .
(13)
.
(13)
Зависимость
тока i
от времени также имеет вид затухающих
колебаний. Это вытекает из формул (3),
(6). Причем в случае слабого затухания
(2 << 02)
колебания тока опережают по фазе
колебания напряжения
![]() на /2:
на /2:
![]() ,
,
где
![]() .
График
.
График![]() для этого случая приведен на рис. 2б.
для этого случая приведен на рис. 2б.
При
2 02
вместо колебаний в контуре происходит
апериодический (непериодический) процесс
установления стационарных значений
тока
![]() и напряжения
и напряжения![]() .
Условие прекращения колебаний
.
Условие прекращения колебаний![]() можно также записать в виде неравенства
можно также записать в виде неравенства![]() ,
где
,
где
![]()
- так называемое критическое сопротивление контура.
