
Подготовка к работе
1. Физические понятия, величины, законы, знание которых необходимо для успешного выполнения работы:
Электрический заряд и его фундаментальные свойства.
Плотность заряда (линейная, поверхностная, объемная).
Закон Кулона.
Пробный заряд. Вектор напряженности электрического поля.
Потенциальность электростатического поля. Разность потенциалов. Потенциал.
Принцип суперпозиции электрических полей.
Связь напряженности поля и потенциала.
Силовая линия. Эквипотенциальная поверхность.
Теорема Гаусса.
Приведите в конспекте вывод формул (1) - (5).
Изучите экспериментальную часть работы. Приведите в рабочей тетради электрическую схему измерений.
Расчетное задание.
Рассчитайте
при помощи (2) зависимость
![]() от
от![]() (
(![]() 5 см,
5 см,![]() 15 см)
и постройте на миллиметровой бумаге
график этой зависимости.
15 см)
и постройте на миллиметровой бумаге
график этой зависимости.
Рекомендуемая литература
И.Е. Иродов. Электромагнетизм. Основные законы. Москва-Санкт-Петербург: ФИЗМАТЛИТ, 2001. §1.1-1.6.
Савельев И.В. Курс общей физики. Электричество и магнетизм. Москва.: Астрель. АСТ, 2001, §§ 1.1-1.8, 1.13, 1.14.
Приложение 1
Рассмотрим
электростатическое поле, созданное в
вакууме системой заряженных проводников.
Электростатическое поле потенциальное,
поэтому для произвольного замкнутого
контура
![]() :
:
![]() .
(П1)
.
(П1)
По теореме Гаусса
![]() ,
(П2)
,
(П2)
где
![]() -
произвольная замкнутая поверхность,
внутри которой отсутствуют заряды. Из
уравнений (П1), (П2) можно получить
дифференциальное уравнение
-
произвольная замкнутая поверхность,
внутри которой отсутствуют заряды. Из
уравнений (П1), (П2) можно получить
дифференциальное уравнение
![]() ,
(П3)
,
(П3)
относительно
потенциала
![]() ,
которое называется уравнением Лапласа
(детали вывода уравнения (П3) из (П1) и
(П2) здесь нас не интересуют).
,
которое называется уравнением Лапласа
(детали вывода уравнения (П3) из (П1) и
(П2) здесь нас не интересуют).
Пусть теперь пространство между проводниками заполнено слабо проводящей однородной средой. Неизменная во времени разность потенциалов между проводниками поддерживается за счет источников ЭДС; в среде протекает постоянный электрический ток.
И
в этом случае электрическое является
потенциальным, следовательно, справедливо
уравнение (П1). Кроме того, в силу закона
сохранения заряда поток вектора плотности
тока
![]() через произвольную замкнутую поверхность
равен нулю:
через произвольную замкнутую поверхность
равен нулю:
![]() .
.
По
закону Ома
![]() ,
где
,
где![]() - удельная
проводимость, поэтому
- удельная
проводимость, поэтому
![]() .
.
Таким образом для электрического поля постоянных токов, как и в вакууме, выполняются уравнения (П1), (П2), а следовательно и уравнение Лапласа (П3).
Приложение 2
Напряженность
поля в точке, определяемой векторами
![]() и
и![]() ,
равна векторной сумме напряженностей
полей обоих стержней:
,
равна векторной сумме напряженностей
полей обоих стержней:![]() .
.
По теореме Гаусса
![]() .
.
Модуль вектора
![]()
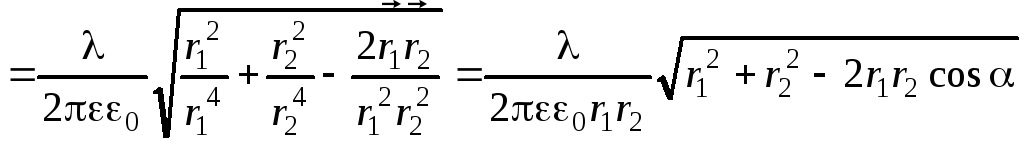 .
.
Квадратный
корень в последнем выражении, как видно
из рис.6, равен (по теореме косинусов)
расстоянию между стержнями 2l
. Поэтому
![]() .
.
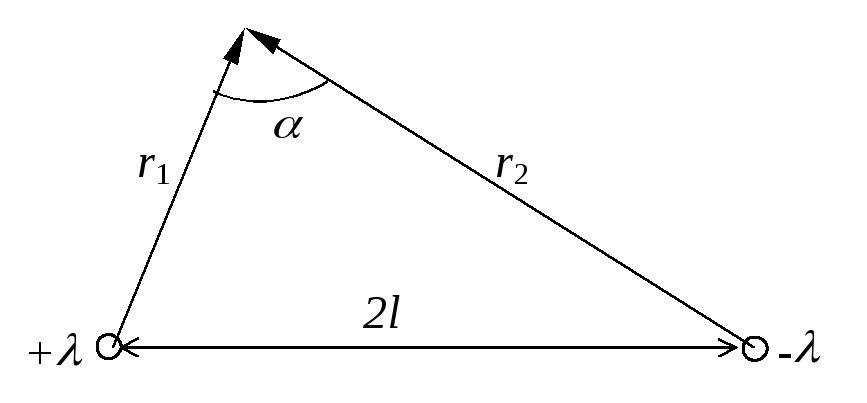
Рис.6. К выводу формулы (4)
