Пример 2.Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов.

Пусть pиq –косоугольный базис, векторы длины один, а угол между ними равен 60^о,a=3p+4q,b=2p-q. Найти скалярное произведение (a,b) , длины векторовaиb..

Решение.

(a,b)=(3p+4q,2p-q)=(3p,2p-q)+(4q,2p-q)=(3p,2p)+(3p,-q)+(4q,2p)+(4q,-q)=

=6(p,p)-3(p,q)+8(q,p)-4(q,q)=6(p,p)+5(p,q)+4(q,q)=6+5-4 =6+5/2-4=4,5

если придать вычислениям общий вид: a=a₁p+a₂q,b=b₁p+b₂q,получим:

*- формула для вычисления скалярного произведения в координатной форме изменилась.

(a,a)=( 3p+4q, 3p+4q)= 9(p,p)+2*12*(p,q)+16(q,q)=9+2*12*+16=37.

.

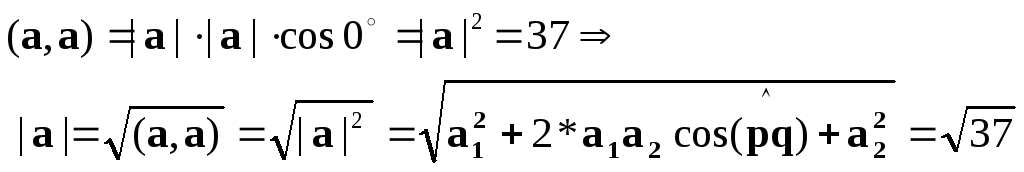- скалярный квадрат по-прежнему равен квадрату длины вектора,

но вычисляются они теперь по-другому.

(b,b)=( 2p-q, 2p-q)= 4(p,p)-4(p,q)+(q,q)=4-2*2*+1=3.

.

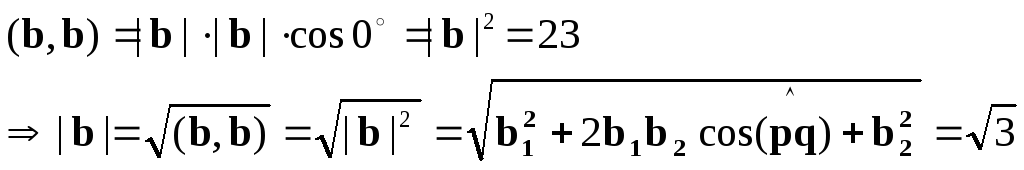Ответ. (a,b)=3,,.

Пример 3.Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.

Пусть pиq–косоугольный базис, причем длины векторов равны 2 и 3 соответственно, а угол между ними равен 60^о,a=3p+4q,b=2p-q. Найти скалярное произведение (a,b) , длины векторовaиb..

Решение.

(a,b)=(3p+4q,2p-q)=(3p,2p-q)+(4q,2p-q)=(3p,2p)+(3p,-q)+(4q,2p)+(4q,-q)=

=6(p,p)-3(p,q)+8(q,p)-4(q,q)=6(p,p)+5(p,q)+4(q,q)=6*2*2+5*2*3*–4*3*3= =24+15–36=3

если придать вычислениям общий вид: a=a₁p+a₂q,b=b₁p+b₂q,получим:

+ *- формула для вычисления скалярного произведения в координатной форме снова изменилась.

(a,a)=( 3p+4q, 3p+4q)= 9(p,p)+24(p,q)+16(q,q)=

= =

=9*2*2+24*2*3*+16*3*3=252.

.

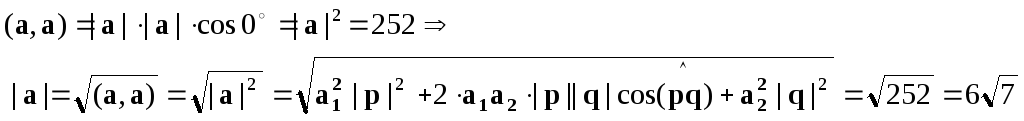(b,b)=( 2p-q, 2p-q)= 4(p,p)-4(p,q)+(q,q)=4*2*2-4*2*3*+3*3=13.

.

Ответ. (a,b)=3,,.

В примерах 1,2 и 3 показано как усложняются расчеты вычисления скалярного произведения векторов и длины вектора в косоугольной системе координат по сравнению с декартовой прямоугольной системой координат.

10. Скалярное произведение в координатной форме

Выше в примерах 1,2,3 мы фактически предвосхитили тему данного параграфа.

Теорема 3.Пусть ,, – декартов базис, , . Тогда .

Доказательство.Имеем

.

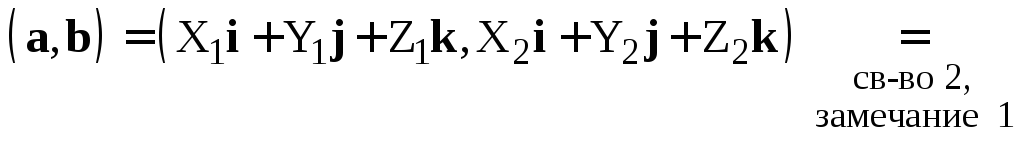
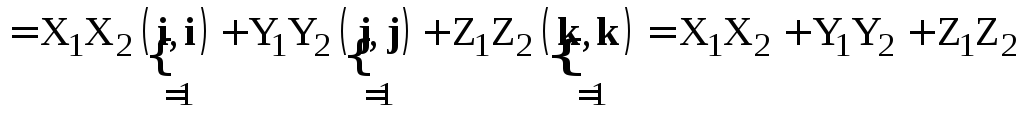Следствие.Пусть,,–декартов базис,,,,. Тогда

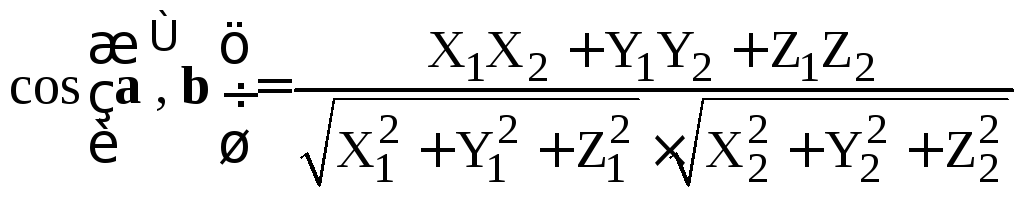. (5)

В самом деле, из формулы (2.1), определяющей скалярное произведение, находим

,

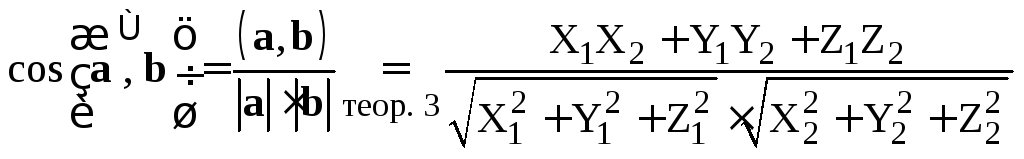и соотношение (5) доказано.

В частности, .

Скалярное произведение двух векторов a и b заданных в координатной форме в MATLAB мы будем вычислять различными способами:

1. Создать формулу, обращаясь индексами к элементам массива

2. Вычислить с помощью поэлементного умножения «.*» произведения соответствующих координат, убедиться, что вычисления соответствуют ожидаемым, затем применить к результату функцию sum.

3. Затем сразу применить обе операции ab=sum(a.*b).

4. В matlabесть стандартная функция, вычисляющая скалярное произведениеdot()

Упражнение 26. Скалярное произведение в координатной форме.

Вычислить скалярное произведение двух векторов a={x1,y1,z1}, b={x2,y2,z2}

>> syms x1 x2 y1 y2 z1 z2

>> a=[x1,y1,z1];b=[x2,y2,z2];

Далее самостоятельно:1,2 3 и 4 способы.

Упражнение 27. Скалярное произведение в прямоугольном и косоугольном базисе.

Выразить скалярное произведение векторов ,_{, то есть},

A) в декартовом базисе,и

B) косоугольном базисе,и. Пользуясь геометрическим свойством скалярного произведения, убедиться, что векторыa,b,cобразуют косоугольный базис.

C) в прямоугольном, но не в ортонормированном базисе,и

Определение скалярного произведения через понятие проекции.

Заметим, что в формуле (1) ,

если принять за орт вектора,

и ,

поэтому можно дать определение скалярного произведения ив иной, равносильной форме, иногда более удобной.

Определение .Скалярным произведением векторов и называется число, равное проекции одного вектора на другой, умноженной на длину последнего.

. (6)

Упражнение 28. Определение скалярного произведения через понятие проекции.

Пусть ,–декартов базис, a=3i+4j,b=2i-j. Сделать геометрическую интерпретацию, определения.

11. Задание для самостоятельной работы

1. Выполнить в тетради и в MATLABвсе упражнения данного практикума.

2. Ответить на контрольные вопросы (некоторые темы изучить самостоятельно). Уметь отвечать на вопросы по темам лабораторной работы и по темам презентаций, даже если презентацию вы не готовите.

3. Подготовить краткую презентацию (5–7 минут) с применением графических средств MATLAB, и выступить с ней у доски. Презентация должна включать в себя вопросы к аудитории.

Темы для презентаций:

1) Орт вектора, направляющие косинусы вектора.

2) Расстояние между векторами.

3) Проекция вектора на ось, свойства, декартов базис.

4) Физический смысл скалярного произведения (найти, рассказать)

Задачи для презентаций:

1. Танковый биатлон.

Ведется огонь по некоторой цели. Цель представляет собой стальной плоский лист толщиной 200 мм,  внешняя поверхность листа лежит на плоскости ZY. Координаты орудия в метрах {30, 30, 2}, огонь ведётся по точке {0, 0.5, 0.3}  (в метрах). Найти толщину листа по прямолинейной траектории полета снаряда от момента вхождения в цель до момента выхода из цели. Для решения задачи создать скрипт, в котором можно быстро изменить входные параметры.

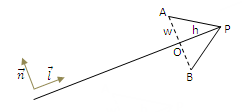
2. Заданы начало и конец отрезка. Необходимо нарисовать стрелку с усиками, ширина раствора которых равна w, а высотаh(см. рисунок). Тригонометрию использовать нельзя (подобное ограничение часто возникает во встраиваемых системах, где вычисление тригонометрических функций слишком дорого по времени). Проиллюстрировать скриптом в матлабе.