Размещение нескольких рисунков в одном графическом окне.
Команда subplot(n1,n2,n)разбивает графическое окно Figures на несколько графических областей одинакового размера:n1 - число областей по горизонтали,n2 - число областей по вертикали,n-выбор области, в которой предстоит строить (в отличии от матриц нумерация идёт по строкам).
Пример 1. Разбиение графического окна на несколько областей.
Создать графическое окно для четырёх координатных плоскостей. В первых трёх построить по одному отрезку, в четвертой все три.
(0,0)______(2,1) , (0,0)______(-1,2), (-2,-4)______(0,0)
>> figure
>> subplot (2,2,1)
>> grid on, axis equal
>> line([0;2],[0;1])
>> subplot (2,2,2)
>> grid on, axis equal
>> line([0;-1],[0;2])
>> subplot (2,2,3)
>> grid on, axis equal
>> line([-2;0],[-4;0])
>> subplot (2,2,4)
>> grid on, axis equal, line([0,0,-2;2,-1,0],[0,0,-4;1,2,0])
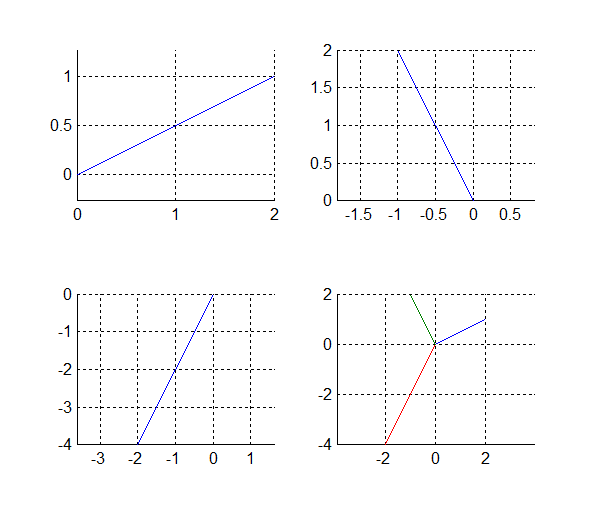
Рис.8
Упражнение 3. Для самостоятельной работы (тетрадь+MATLAB)
Создать графическое окно для четырёх координатных плоскостей. В третьей области построить все три отрезка, в остальных по одному.
Прямые:
(0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
Построение векторов на плоскости.
Если требуется изобразить вектор, то есть отрезок со стрелкой на конце, можно воспользоваться функцией quiver(). Ее формат следующий:
quiver(x_begin, y_begin, x_comp, y_comp, scale, LineSpec),
где x_beginиy_beginэто массив абсцисс и ординат начал векторов, аx_compиy_comp– компоненты векторов.Параметр scale мы будем принмать равным 1.
Функция quiver часто используется для построения большого количества векторов (т. н. векторных полей), где важны не столько длины векторов, сколько их визуальное соотношение. Параметр scale позволяет упростить анализ векторных полей. Однако мы эту функцию используем для точного отображения векторов, поэтому у нас scale всегда равен 1.
Если нужно построить вектора разными цветами, для каждого цвета следует использовать отдельную функцию quiver.
Команды графики, такие как plot, quiver, surf и т.д. стирают предыдущие изображения, включение режима добавления графиков «hold on» позволяет этого избежать.
Пример 2. Векторы на плоскости
Построим следующие векторы:
(0,0)______(2,1) , (0,0)______(-1,2), (0,0)______(-2,-4)
Толщину последнего положим равной 4.
Первые два аргумента функции quiver – начало вектора – совпадает с первой точкой отрезка. Вторые два аргумента – компоненты вектора – есть разность начальной и конечной точек отрезка. В данном случае компоненты совпадают с конечной точкой отрезка.
>> figure, grid on, axis equal, hold on
>> quiver(0, 0, 2, 1, 1)
>> quiver(0, 0, -1, 2, 1, 'g')
>> quiver(0, 0, -2, -4, 1, 'r', 'lineWidth', 4)
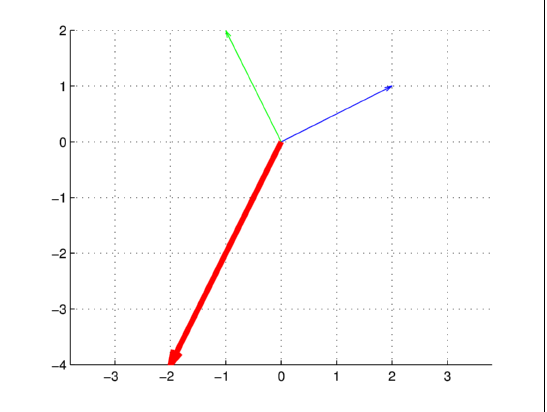
Рис.9
Другой способ рисования векторов заключается в последовательном использовании функций line() для рисования отрезка и функции plot(x,y,’>’,’LineWidth’,4) для рисования стрелки
Координаты x,yвplot- это координаты точки на плоскости (в нашем случае точки конца вектора).
В первых одинарных кавычках можно разместить ‘маркер, цвет, тип линии’, в нашем случае размещён только маркер - треугольник, тип линии нам пока не нужен. Команды «^,<,>,v» задают треугольники, которыми удобно помечать концы векторов. «LineWidth» задаёт толщину маркера. См. вышетаблицу 1.
Пример 3. Векторы на плоскости (тетрадь+matlab)
Построим векторы, взяв за их основу отрезки с соответствующими началом и концом:
(0,0)______(2,1) , (0,0)______(-1,2), (0,0)______(-2,-4)
отметив «концы-стрелочки» в соответствующих точках.
При добавлении в функцию lineопции «'Color',[код цвета в палитре RGB]», можно влиять на цвет линии. Цвет выбирается на основании таблицы 3.
>> figure, grid on, axis equal, hold on
>> line([0,0;2,-1],[0,0;1,2])
>> line([0; -2], [0 -4], 'lineWidth', 4, 'Color', [1 0 0])
>> plot(2,1,'>b','lineWidth',4)
>> plot(-1,2,'^g','lineWidth',4)
>> plot(-2,-4,'vr','lineWidth',4)
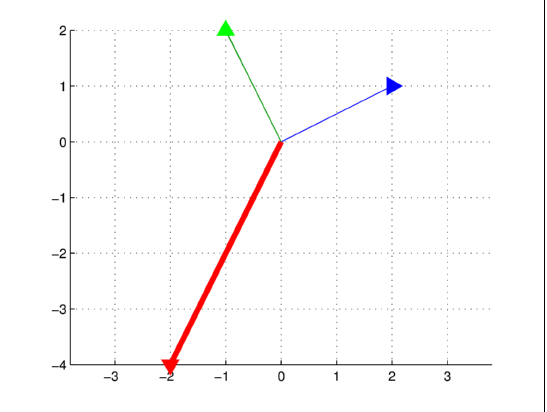
Рис.10
Хороший стиль
Очевидно, что оба способа рисования векторов подходят только для случая, когда необходимо различать начало и конец отрезка. В случае, когда нужна стрелка указания некоторого элемента на графике, лучше всего воспользоваться сторонней функцией arrow. Скачать её можно здесь. Вот пример реализованного функционала:
Упражнение 4. Для самостоятельной работы. (тетрадь+matlab)
Построить следующие векторы (0,0)____(2,1), (0,2)_____(2,0),(0,2)_____(3,0). Можно пользоваться quiver и line+plot по выбору. Все векторы покрасить в чёрный цвет, установить толщину 3.
Векторы на графике можно подписать, используя команду text(), входными параметрами вtextслужат координаты точки, в которой будет стоять надпись, саму надпись пишем в фигурных скобках в одинарных кавычках. Пометим векторы из предыдущего упражнения. Синий будет векторомa, зелёный - b, красный -c.
text(2.5,1.5,'\bfa') % добавление полужирного обозначения вектора
text(-1.5,2.5,'\bfb')
text(-2.5,-3.5,'\bfc')
text(2.5,0.5,'a') % добавление обычного обозначения вектора
text(-1.5,1.5,'b')
text(-2.5,-4.5,'c')
Добавление перед текстом письма «\bf» позволяет сделать текст полужирным, (векторы принято обозначать полужирными буквами). Ниже на рисунке 7 посмотрите разницу между пометками векторов полужирными и обычными буквами.
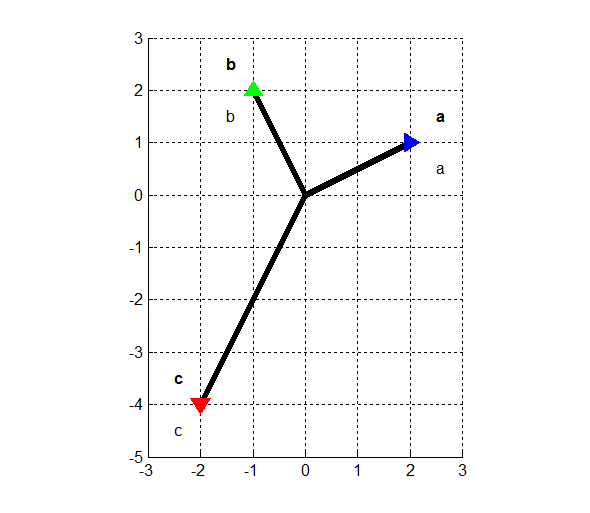
Рис.12
Для того чтобы в одном выражении написать полужирные и обычные символы, выделяемые полужирным символы заключают в фигурные скобки, например, для того чтобы добавить запись, c = 1 i — 4 j, запишем следующее
text(-1.6,-4.3,'{\bfc} = 1 {\bfi}-4 {\bfj}')
и получим:
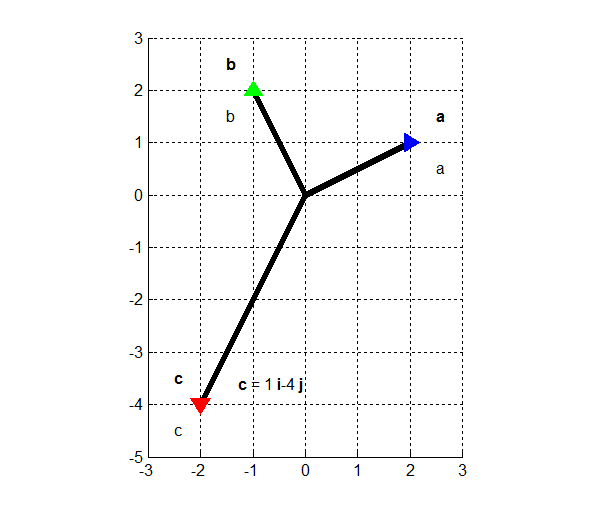
Рис.13.