
- •Порядок выполнения.
- •Геометрические векторы и линейные операции над ними.
- •Свойства операции сложения геометрических векторов:
- •Построение векторов в графическом окне matlab.
- •Построение прямых. Команда line.
- •Размещение нескольких рисунков в одном графическом окне.
- •Пример 1. Разбиение графического окна на несколько областей.
- •Построение векторов на плоскости.
- •Пример 2. Векторы на плоскости
- •Построение векторов в пространстве.
- •Скрипты, м – файлы.
- •Создание Script m–Files
- •Упражнение 6. Для самостоятельной работы.
- •Упражнение 7. Для самостоятельной работы.
- •Упражнение 8. Правило треугольника.
- •Упражнение 9. Правило параллелограмма.
- •Упражнение 10. Сумма и разность векторов.
- •Логическое равенство.
- •Упражнение 11. Свойства суммы векторов
- •Упражнение 12. Проверить свойства умножения вектора на число.
- •Длина вектора
- •Упражнение 13. Длина вектора, орт вектора. Пространство.
- •Упражнение 14. Длина вектора, орт вектора. Плоскость.
- •Направляющие косинусы
- •Определение
- •Упражнение 18. Изобразить векторы базиса. Пространство.
- •Упражнение 19. Изобразить векторы базиса. Плоскость.
- •Упражнение 20. Разложение вектора по двум неколлинеарным векторам.
- •Упражнение 21. Разложение вектора по трем некомпланарным векторам.
- •Упражнение 22. Линейная зависимость четырёх векторов.
- •Косоугольная и прямоугольная система координат.
- •Скалярное произведение векторов
- •Пример 2.Вычисление скалярного произведения в косоугольном базисе, состоящем из единичных векторов.
- •Пример 3.Вычисление скалярного произведения в косоугольном базисе, состоящем из векторов произвольной длины.
- •Скалярное произведение в координатной форме
- •Упражнение 26. Скалярное произведение в координатной форме.
- •Контрольные вопросы
- •Контрольное мероприятие № 1. Защита л.1.1 и л.1.2.
- •Индивидуальные задания № 1 Векторная алгебра.
- •Список рекомендуемой литературы
Свойства операции сложения геометрических векторов:
1) для любых двух
геометрических векторов
![]() и
и![]() :
:
![]() - переместительное
или коммутативное свойство;
- переместительное
или коммутативное свойство;
2) для любых трёх
геометрических векторов
![]() ,
,![]() и
и![]() :
:
![]() - сочетательное
или ассоциативное свойство
- сочетательное
или ассоциативное свойство
(коммутативность от латинского commutativus - «меняющийся»)
(ассоциативность от латинскогоassociatio - соединение).
Построение векторов в графическом окне matlab.
Построение прямых. Команда line.
С самого начала мы будем использовать визуализацию: изображать векторы (отрезки) на плоскости и в пространстве. Для этого мы будем использовать функции line(используется как в плоскости, так и в пространстве) иplot(для плоскости, для пространства аналогом будетplot3).
>> help line
>> help имя команды - позволяет узнать информацию об этой команде.
line([x1; x2],[y1; y2], 'Color','r','LineWidth',4).
Color- цвет, по умолчанию он синий.
LineWidth- толщина линии в пунктах, один пункт равен 1/72 дюйма. По умолчанию ширина линии равна 0.5 пункта.
Ниже в таблице1 приведены обозначения цветов, типов линий и маркеров. Таблица 1 будет полезна не только для функции line, но и для других команд, отвечающих за графику.
|
Таблица 1. |
| |||||
|
Цвет линии и маркера [код цвета в палитре RGB]
|
Тип маркера |
Тип линии | ||||
|
b |
синий (blue) |
[001] |
. |
точка |
- сплошная | |
|
g |
зеленый (green) |
[010] |
o |
круг |
: пунктирная | |
|
r |
красный (red) |
[100] |
x |
|
-. штрих-пунктирная | |
|
c |
голубой (cyan) |
[011] |
+ |
плюс |
-- штриховая | |
|
m |
фиолетовый (magenta) |
[101] |
* |
звезда |
| |
|
y |
желтый (yellow) |
[110] |
s |
квадрат (square) |
| |
|
k |
черный (black) |
[000] |
d |
ромб (diamond) |
| |
|
w |
белый (white) |
[111] |
p |
пятиконечная звезда (pentagram) |
| |
|
|
|
|
h |
шестиконечная звезда (hexagram) |
| |
|
|
|
|
^,<,>,v |
треугольники |
| |
Итак, функция lineпозволяет строить на координатной
плоскости прямые (отрезки) по точкам,
координаты которых являются входными
аргументами в функцию. Если нам надо
изобразить отрезок с началом в точке![]() и концом в точке
и концом в точке![]() Мы
должны записать в первых квадратных
скобках абсциссу начальной точки, затем через точку запятой абсциссу
конечной точки, далее через запятую в
следующих квадратных скобках аналогичные
данные по ординатам. Далее через запятую
определённым образом записываются
свойства линии (если мы хотим изменить
свойства, имеющиеся по умолчанию)
Мы
должны записать в первых квадратных
скобках абсциссу начальной точки, затем через точку запятой абсциссу
конечной точки, далее через запятую в
следующих квадратных скобках аналогичные
данные по ординатам. Далее через запятую
определённым образом записываются
свойства линии (если мы хотим изменить
свойства, имеющиеся по умолчанию)
При выполнении упражнений сначала все проделать у себя в тетради, затем в MATLAB.
Упражнение 1. Функция line(тетрадь+MATLAB)
Построить три отрезка
(0,0)______(2,1) , (0,0)______(-1, 2), (-2,-4)______(0,0) .
Решение:
Задаём первую прямую (0,0)______(2,1)
с началом в точке
![]() и концом в точке
и концом в точке![]() ,
,
задаём аргументы функции line([0;2],[0;1]),
для второго и третьего отрезков задайте аргументы функции самостоятельно
После ниже следующих команд сразу появится графическое окно Figures. Закрепите окно Figures над Command Window, для этого щелкните левой кнопкой мыши по стрелочке Dock Figure в правом верхнем углу графического окна.
>> line([0;2],[0;1]), line(), line()
Для того чтобы легче было воспринимать картинку добавим команды для оформления графика. Включите сетку командой «grid on» и введите одинаковый масштаб по осям «axis equal»
>> grid on, axis equal
В итоге у Вас должно получиться, см. Рис.6.
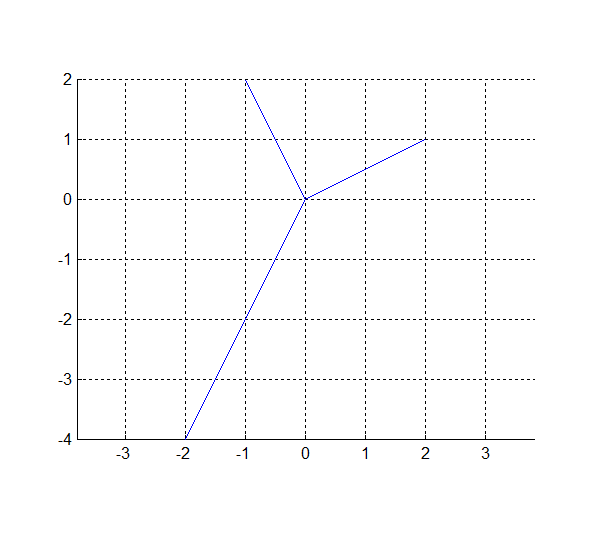
Рис.6.
По умолчанию функция lineизобразила отрезки синим цветом.
Скопируйте рисунок в отчёт. Для того чтобы скопировать рисунок в файл, сделайте активным графическое окно, в меню выберете Edit → Copy Figure.
Закройте окно Figures.
Если надо нарисовать несколько прямых в одной команде
(X10,Y10)____(X1,Y1),
(X20,Y20)_____(X2,Y2),
(X30,Y30)_____(X3,Y4),
то нужно записать координаты векторов в определённой последовательности:
line([абсциссы начал;абсциссы концов],[ординаты начал; ординаты концов])
line([X10, X20, X30; X1, X2, X3],[ Y10,Y20,Y30; Y1, Y2, Y3])
Для того чтобы всякий раз не закрывать графическое окно, а новый объект изображался в новом графическом окне, перед командами, отвечающими за очередное построение нужно ввести
>> figure
Упражнение 2. Для самостоятельной работы. (тетрадь+matlab)
Постройте три отрезка (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) с помощью одной команды line.
