Практикум по линейной алгебре и аналитической геометрии в среде МАТЛАБ.

Модуль 1. Аналитическая геометрия.

Цель модуля.С помощью графических иллюстрацийMATLABосвоить фундаментальные понятия векторной алгебры и аналитической геометрии.

Лабораторный практикум 1.2. Векторная алгебра.

Цели работы. Работа с графикой: построение векторов на плоскости и в пространстве. Работа с М-файлами. Приобретение навыков решения задач векторной алгебры с помощью средств системы MATLAB. Освоение с помощью графических иллюстраций MATLAB фундаментальных понятий векторной алгебры:

геометрический вектор, линейные операции над векторами,

длина вектора, орт вектора, направляющие косинусы,

линейная зависимость двух, трех, четырех и более векторов,

понятие базиса, проекция векторов на ось,

прямоугольная и косоугольная системы координат,

скалярное произведение векторов.

Продолжительность работы. 4 академических часа в аудитории и 4 часа на самостоятельную работу (2 недели)

Срок сдачи: 4,5 недели.

Оборудование, приборы, инструментарий.Письменная часть работы выполняется в тетради, электронная часть работы выполняется в компьютерном классе с использованием пакета MATLAB.

Порядок выполнения.

1. Упражнения выполняются параллельно с изучением теоретического материала из параллельного курса «Линейная алгебра и аналитическая геометрия», см. приложения, лекции и другую литературу.

2. Большинство упражнений необходимо предварительно решать в тетради.

3. При выполнении упражнений в случае появления сообщения об ошибке рекомендуется сначала самостоятельно выяснить, чем оно вызвано, и исправить команду; если многократные попытки устранить ошибку не привели к успеху, - проконсультироваться с преподавателем.

4. Дома доделать примеры и упражнения, которые Вы не успели выполнить во время занятия; выполнить дополнительные упражнения для самостоятельной работы и ответить на контрольные вопросы.

5. Подготовить отчёт, в который включить результаты по упражнениям и развернутые ответы на контрольные вопросы. Отчёт представить в виде документа Microsoft Word, имя файла (пример): «мп_17_Иванов_Павел_лаб_1_1» (факультет_группа_Фамилия студента_Имя студента_номер лабораторной). По каждому выполненному упражнению отчет должен содержать:

12. № упражнения; текст упражнения;

13. команды, скопированные из командного окна, с комментариями к ним

14. результаты их выполнения, включая построенные графики;

15. выводы и комментарии к полученным результатам.

*Без предъявления письменных решений электронный отчет не рассматривается. **При проверке решений и отчета у преподавателя не должно возникать необходимости обращаться к источнику задания.

1. Геометрические векторы и линейные операции над ними.

Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке (т. е. указано, какая из его граничных точек является началом, а какая - концом).

Векторы обозначают символом, либо одной малой полужирной латинской буквой, например,, Если за начало отрезкапринята точка, то точкуназываютточкой приложениявектора.

На чертеже (рис. 1.) вектор изображен отрезком со стрелкой в конечной точкеB.

Длинойвектораназовем длину отрезкаи в записи используем знак абсолютной величины:(либо).

Вектор называетсянулевымвектором, если его конечная точкасовпадает с начальной.

Нулевой вектор, в силу его определения, не имеет направления, а длина его равна нулю.

Векторы иназовемколлинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2).

Два вектора иназываютравными, если они коллинеарны, имеют общее направление и равные длины (рис. 3).

Из определения следует, что два вектора, равные третьему, равны между собой (Рис. 3.) Именно поэтому в аналитической геометрии не различают равные векторы, имеющие разные точки приложения. Векторы, изучаемые в аналитической геометрии, называются свободными. Обычно их и обозначают малой полужирной латинской буквой, например. Векторы, приложенные к какой-то точкеили, называютсязакрепленными.

Напомним, что сумма двух векторов может быть найдена:

а) по правилу треугольника; б) по правилу параллелограмма (см. рис. 4).

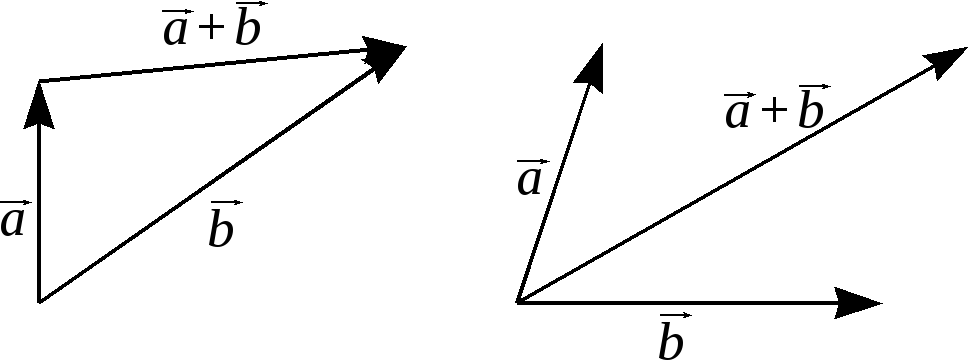
Рис.4.

Если векторы иколлинеарны, то “работает” только первое правило.

Кроме того, для любых точек M,N,Pплоскости или пространства имеет место правило трёх точек:(см. рис. 5).

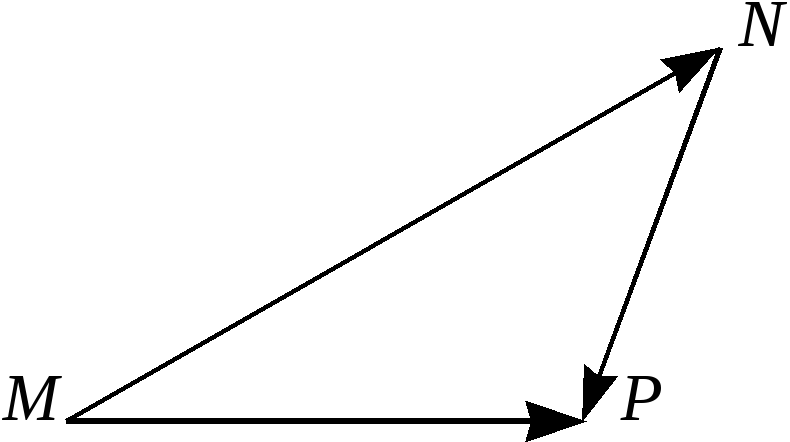
Рис.5.