
- •Часть 3. Системы дифференциальных уравнений.
- •Занятие 13. Системы дифференциальных уравнений в нормальной форме. Понятие общего решения. Задача Коши для системы. Решение системы сведением к одному ду более высокого порядка.
- •Занятие 14. Решение системы ду методом Эйлера.
- •Занятие 15. Решение системы дифференциальных уравнений: методом неопределённых коэффициентов и методом вариации произвольных постоянных.
- •Занятие 16. Исследование устойчивости решений однородных систем с постоянными коэффициентами. Исследование устойчивости по первому приближению.
- •Исследование устойчивости по первому приближению
Занятие 15. Решение системы дифференциальных уравнений: методом неопределённых коэффициентов и методом вариации произвольных постоянных.
|
Ауд. |
Л-4. Гл. 10 |
№ 442, 444, 445. |
3 |
☺ ☻ ☺
Общие сведения. Для моделирования общего алгоритма решения системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами рассмотрим систему, содержащую только три уравнения для функций x,y,z:
 (1)
(1)
где функции
![]() ,
,![]() ,
,![]() – непрерывные функции переменной
– непрерывные функции переменной
![]() ,
заданы в соответствии с правилом (4) и
хотя бы одна из
них не равна нулю. Функции
,
заданы в соответствии с правилом (4) и
хотя бы одна из
них не равна нулю. Функции
![]() ,
,![]() ,
,![]() – искомые решения.
– искомые решения.
Общий алгоритм решения неоднородного уравнения:
1*.
Записываем соответствующую неоднородной
системе уравнений (1) однородную систему
(без функций
![]() ,
,![]() ,
,![]() ):
):  (2)
(2)
и находим её решение (в соответствии с представленными в Главе Пособия 12 методами).
2*.
Находим частное решение системы (1)
однородную систему, учитывая конкретный
набор функций
![]() ,
,![]() ,
,![]() .
.
3*.
Записываем общее решение системы (4) в
виде: ![]() =
=![]() +
+![]() . (3)
. (3)
4*. Находим решение системы (1), удовлетворяющее заданным начальным условиям.
Записанный алгоритм
содержит величины:
![]() ,
,![]() ,
,![]() ,
вычисление которых зависит и от набора
функций:
,
вычисление которых зависит и от набора
функций:
![]() ,
,![]() ,
,![]() ,
и от особенностей заданной системы (1).
Не станем записывать общих формул,
которые охватили бы самый общий набор
функций
,
и от особенностей заданной системы (1).
Не станем записывать общих формул,
которые охватили бы самый общий набор
функций
![]() ,
,![]() ,
,![]() и получающихся выражений для вычисления
функций:
и получающихся выражений для вычисления
функций:
![]() ,
,![]() ,
,![]() .
Правила решения системы (1) вполне понятны
из рассмотрения конкретных Примеров!
.
Правила решения системы (1) вполне понятны
из рассмотрения конкретных Примеров!
••• ≡ •••
Пример
1–442:
Решить
систему нелинейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функции
![]() ):
):
![]() =
=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =1–i;
=1–i;
![]() =1+i.
В этом случае общее решение однородной
системы будем искать в виде:
=1+i.
В этом случае общее решение однородной
системы будем искать в виде: ![]() =
=![]()
![]() +
+![]()
![]() , (1)
, (1)
где
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() . (2)
. (2)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
 (3)
(3)
3). Для
![]() =1–i
система (3) имеет решение:
=1–i
система (3) имеет решение:
![]() =
=![]() .
Тогда можно записать:
.
Тогда можно записать:
![]() =
=![]() ∙
∙![]() =
=![]() =
= . (4)
. (4)
4). Для
![]() =1+i
система (3) имеет решение:
=1+i
система (3) имеет решение:
![]() =
=![]() .
Аналогично получаем:
.
Аналогично получаем:
![]() =
=![]() ∙
∙![]() =
=![]() =
= . (5)
. (5)
т.е. решения
![]() и
и
![]() – комплексно-сопряженные.
– комплексно-сопряженные.
5). В качестве
частных решений системы уравнений берем
отдельно мнимую и действительную части.
Получаем: ![]() =
=![]() ,
,
![]() =
=![]() (6)
(6)
6). С учетом выражений
(6) запишем общее решение однородной
системы дифференциальных уравнений:
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() .
(7)
.
(7)
7). Так как функция:
![]() – имеет специальный вид, ее образующее
число
– имеет специальный вид, ее образующее
число
![]() =
=![]() не совпадает с характеристическими
корнями
не совпадает с характеристическими
корнями
![]() и
и
![]() ,
то частное решение заданной системы
будем искать в виде:
,
то частное решение заданной системы
будем искать в виде: ![]() =
=![]() ,
ее производные:
,
ее производные: ![]() =
=![]() . (8)
. (8)
8). Подставляя (8) в заданную систему, получаем систему тождеств:
![]() откуда следует:
откуда следует:
![]() =–1,
=–1,
![]() =0. (9)
=0. (9)
9). Запишем общее решение заданной неоднородной системы:
![]() =
=![]() +
+![]() =
=![]()
![]() ∙
∙![]() +
+![]() ∙
∙![]() ∙
∙![]() +
+![]() ∙
∙![]() =
= ∙
∙![]() .
(10)
.
(10)
Ответ:
общее решение:
![]() =
=
 ∙
∙![]() .
.
Пример
2–444:
Решить
систему нелинейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функций
![]() =
=![]() и
и
![]() =
=![]() ):
∆(k)=
):
∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() ,
,
![]() =
=![]() .
В этом случае общее решение однородной
системы будем искать в виде:
.
В этом случае общее решение однородной
системы будем искать в виде:
![]() =
=![]()
![]() +
+![]()
![]() ,
(1)
,
(1)
где
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() , (2)
, (2)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
 (3)
(3)
3). Для значения
![]() =
=![]() =
=![]() система (3) имеет решение:
система (3) имеет решение:
![]() =
=![]() .
Тогда можно записать:
.
Тогда можно записать:
![]() =
=![]() ∙
∙![]() =
=![]() =
= . (4)
. (4)
4). Для значения
![]() =
=![]() =
=![]() система (3) имеет решение:
система (3) имеет решение:
![]() =
=![]() .
Аналогично получаем:
.
Аналогично получаем:
![]() =
=![]() ∙
∙![]() =
=![]() =
= , (5)
, (5)
то есть решения
![]() и
и
![]() (выражения (4)и (5)) комплексно-сопряженные.
(выражения (4)и (5)) комплексно-сопряженные.
5). В качестве
частных решений системы уравнений берем
отдельно мнимую и действительную части.
Получаем: ![]() =
=![]() ,
, ![]() =
=![]() . (6)
. (6)
6). С учетом выражений
(6) запишем общее решение однородной
системы дифференциальных уравнений:
![]() =
=![]()
![]() +
+![]()
![]() .
(7)
.
(7)
7). Так как функции:
![]() =
=![]() и
и
![]() =
=![]() – имеют специальный вид и общее образующее
число
– имеют специальный вид и общее образующее
число
![]() ,
причем совпадает с характеристическими
корнями
,
причем совпадает с характеристическими
корнями
![]() и
и
![]() ,
то частное решение заданной системы
будем искать в виде:
,
то частное решение заданной системы
будем искать в виде:
![]() =
=![]() .
(8)
.
(8)
8). Подставляя (8) в заданную систему, получаем систему тождеств:
![]() =
=
=![]() , (9)
, (9)
![]() =
=
=![]() .
.
Приравнивая
коэффициенты при подобных членах
тождеств (9), получим алгебраическую
систему уравнений, решением которой
является:
![]() =–1,
=–1,
![]() =
=![]() =
=![]() =
=![]() =
=![]() =0,
=0,
![]() =
=![]() =1.
Тогда (8) можно записать в виде:
=1.
Тогда (8) можно записать в виде:
![]() =
=![]() (10)
(10)
9). Запишем общее решение заданной неоднородной системы:
![]() =
=![]() +
+![]() =
=
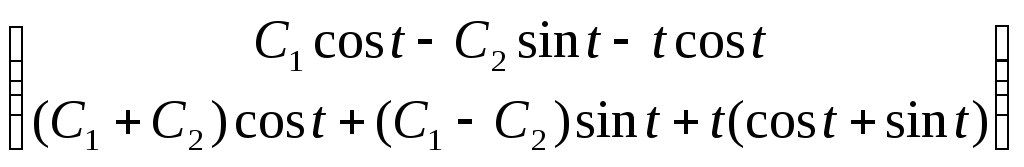 ∙
∙![]() .
(11)
.
(11)
Ответ:
Общее решение:
![]() =
=
 ∙
∙![]() .
.
Пример
3–445:
Решить
систему линейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функций
![]() ,
,![]() ):
):
![]() =
=
![]() = 0, откуда находим:
= 0, откуда находим:
![]() =–i;
=–i;
![]() =i.
=i.
2). В этом случае общее решение однородной системы будем искать в виде:
![]() =
=![]()
![]() +
+![]()
![]() ,
(1)
,
(1)
где
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() , (2)
, (2)
3). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
 (3)
(3)
4). Для
![]() =–i
система (3) имеет решение:
=–i
система (3) имеет решение:
![]() .
Тогда можно записать:
.
Тогда можно записать:
 . (4)
. (4)
5). Для
![]() =i
система (3) имеет решение:
=i
система (3) имеет решение:
![]() .
Аналогично получаем:
.
Аналогично получаем:
 . (5)
. (5)
то есть решения
![]() и
и
![]() – комплексно-сопряженные.
– комплексно-сопряженные.
6). В качестве
частных решений системы уравнений берем
отдельно мнимую и действительную части.
Получаем: ![]() =
=![]() ,
,
![]() =
=![]() (6)
(6)
7). С учетом выражений
(6) запишем общее решение однородной
системы дифференциальных уравнений:
![]() =
=![]()
![]() +
+![]()
![]() .
(7)
.
(7)
8). Для нахождения
искомых функций x(t),
y(t)
применяют метод «вариации произвольных
постоянных. Для этого считают
![]() ,
,
![]() функциями переменной
функциями переменной
![]() ,
которые находят из системы уравнений:
,
которые находят из системы уравнений:  или
или
 (8)
(8)
9). Так как определитель системы (3) не равен нулю, система имеет решение:
 или после
интегрирования:
или после
интегрирования:
 (9)
(9)
где
![]() ,
,
![]() – произвольные постоянные интегрирования.
Подставляя (9) в (7), получим общее решение
неоднородной системы уравнений:
– произвольные постоянные интегрирования.
Подставляя (9) в (7), получим общее решение
неоднородной системы уравнений:
![]() =
=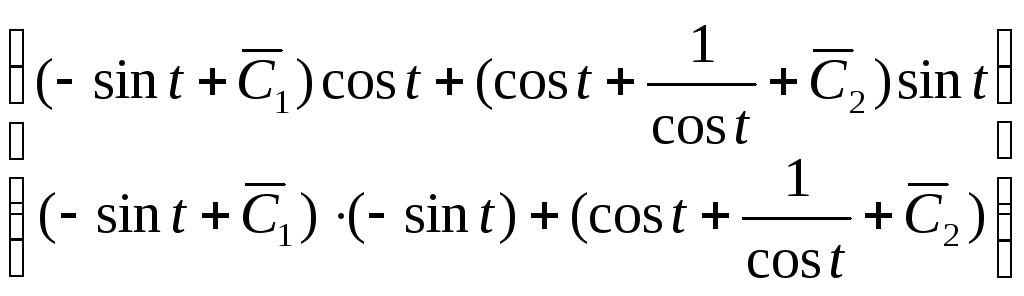 =
= . (10)
. (10)
Ответ:
Общее решение:
![]() =
=
 .
.
Вопросы для самопроверки:
-
Как по записи системы уравнений 1-го порядка определить, что она линейная?
-
Почему линейная система однородных уравнений с постоянными коэффициентами удовлетворяет требованиям теоремы «о существовании и единственности решений»?
-
Как записывают характеристический многочлен для системы линейных однородных уравнений с постоянными коэффициентами?
-
Как записывают общее решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как находят частное решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как учитывают кратность характеристических корней при решении системы линейных однородных уравнений с постоянными коэффициентами?
☺☺
