
- •Часть 3. Системы дифференциальных уравнений.
- •Занятие 13. Системы дифференциальных уравнений в нормальной форме. Понятие общего решения. Задача Коши для системы. Решение системы сведением к одному ду более высокого порядка.
- •Занятие 14. Решение системы ду методом Эйлера.
- •Занятие 15. Решение системы дифференциальных уравнений: методом неопределённых коэффициентов и методом вариации произвольных постоянных.
- •Занятие 16. Исследование устойчивости решений однородных систем с постоянными коэффициентами. Исследование устойчивости по первому приближению.
- •Исследование устойчивости по первому приближению
УЧЕБНАЯ ДИСЦИПЛИНА – «Дифференциальные уравнения».
Часть 3. Системы дифференциальных уравнений.
Занятие 13. Системы дифференциальных уравнений в нормальной форме. Понятие общего решения. Задача Коши для системы. Решение системы сведением к одному ду более высокого порядка.
|
Ауд. |
Л-4. Гл. 10 |
№ 412, 414, 416, 418, 420, 422*, 427 + 431, 432, 438, 440, 444. |
7+5 |
☺ ☻ ☺
Общие
сведения. Учитывая, что в предлагаемых
для самостоятельных упражнений заданиях
мы ограничиваемся системами, состоящими
из двух уравнений, все общие выражения
относим только к системам двух
дифференциальных уравнений: 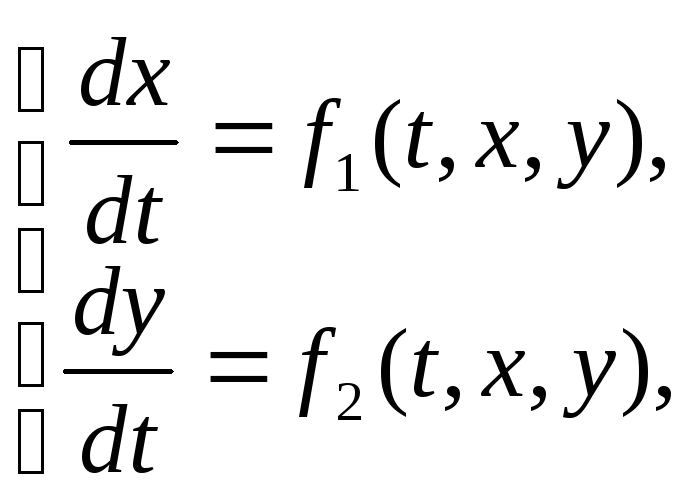 (1)
(1)
где функции
![]() ,
,
![]() – заданные, дифференцируемые.
– заданные, дифференцируемые.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
1). Продифференцируем
уравнения (1.1) и (1.2) системы (1) по
![]() ,
учитывая, что
,
учитывая, что
![]() – некоторые функции независимой
переменной
– некоторые функции независимой
переменной
![]() :
:
![]() . (2)
. (2)
Воспользовавшись уравнениями (1.1) и (1.2), запишем выражение (2) в виде:
![]() . (3)
. (3)
2). Из выражений
(1.1) и (3) составим систему уравнений:
 (4)
(4)
Для удобства, в
системе уравнений (4) принято:
![]() ,
,
![]() .
Применяя общие правила решения системы
уравнений, выразим (считая, что это
возможно!) из уравнения (4.1) функцию
.
Применяя общие правила решения системы
уравнений, выразим (считая, что это
возможно!) из уравнения (4.1) функцию
![]() и подставим её в уравнение (4.2):
и подставим её в уравнение (4.2):
![]() . (5)
. (5)
3). Уравнение (5) –
дифференциальное уравнение 2-го порядка
для функции
![]() .
Решая это уравнение, получим:
.
Решая это уравнение, получим: ![]() , (6)
, (6)
где
![]() ,
,
![]() – произвольные постоянные. Используя
решение
– произвольные постоянные. Используя
решение
![]() ,
вычисляем
,
вычисляем
![]() и записываем:
и записываем: ![]() .
.
4). Используя решения
![]() и
и
![]() ,
оформляем общее решение исходной системы
(1).
,
оформляем общее решение исходной системы
(1).
••• ≡ •••
Пример
1–412:
Решить систему уравнений:
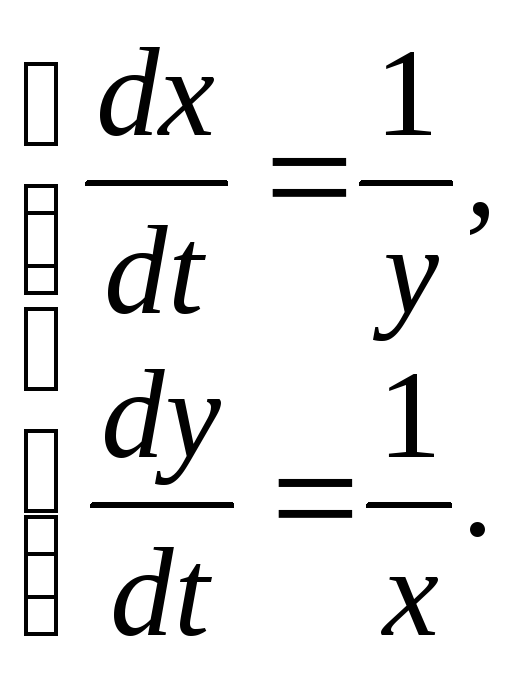 (1)
(1)
Решение:
Замечание:
система уравнений не является линейной,
применим метод сведения системы уравнений
к одному уравнению 2-го порядка относительно
![]() или
или
![]() .
.
1). Продифференцируем
по t уравнение (1.1):
![]() =–
=–![]()
![]() ,
учтём (1.2) →
,
учтём (1.2) →
![]() =–
=–![]()
![]() .
Далее учитываем из (1.1):
.
Далее учитываем из (1.1):
![]() =
=![]() ,
после чего получаем уравнение:
,
после чего получаем уравнение:
![]() ,
или
,
или
![]() .
Последнее равносильно уравнению
.
Последнее равносильно уравнению
![]() .
.
2). Интегрируя
уравнение
![]() ,
получаем:
,
получаем:
![]() =
=![]() ,
или
,
или
![]() .
.
3). Учитывая
уравнение (1.1),
из выражения
![]() =
=![]() получаем:
получаем:
![]() .
.
4). Общее
решение записывается в виде системы:
 .
.
Ответ: общее
решение системы:
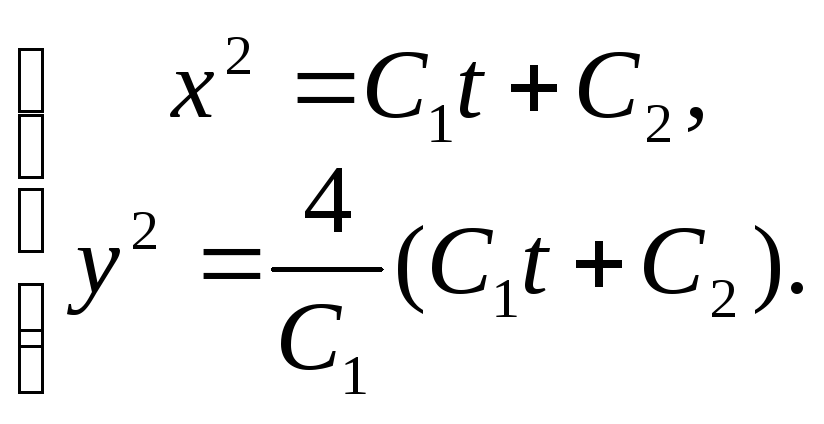 .
.
Пример
2–414:
Решить систему уравнений:
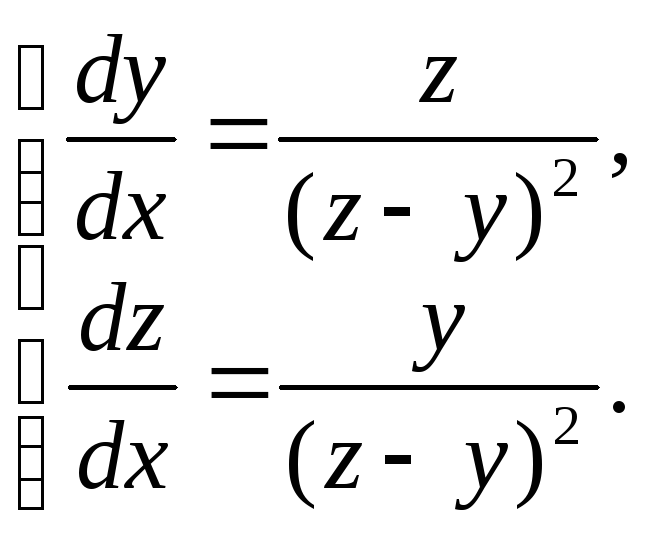 (1)
(1)
Решение:
1). Умножив (1.1)
на
![]() и учитывая (1.2),
получим:
и учитывая (1.2),
получим:
![]() .
Интегрируя последнее, легко получаем:
.
Интегрируя последнее, легко получаем:
![]() .
.
2). Перепишем (1.1),
применяя тождественные преобразования:
![]() =
=![]() =
=![]() +
+![]() .
Учитывая (1.2), запишем:
.
Учитывая (1.2), запишем:
![]() =
=![]() +
+![]() ,
или
,
или
![]() =–
=–![]() .
Последнее уравнение легко интегрируется
(если иметь в виду
.
Последнее уравнение легко интегрируется
(если иметь в виду
![]() ):
):
![]() .
.
3). Используя
выражения
![]() и
и
![]() ,
легко получить (сложив эти выражения!):
,
легко получить (сложив эти выражения!):
![]() .
Модифицируя постоянные:
.
Модифицируя постоянные:
![]() → 2
→ 2![]() ;
;
![]() → 2
→ 2![]() ,
запишем:
,
запишем:
![]() .
Возводя последнее выражение в квадрат,
и учитывая выражение
.
Возводя последнее выражение в квадрат,
и учитывая выражение
![]() ,
получим:
,
получим:
![]() =
=![]() .
Используя
.
Используя
![]() ,
нетрудно получить
,
нетрудно получить
![]() =
=![]() .
.
Замечание: Пример хорошо иллюстрирует возможности импровизации при решении системы ДУ применением метода сведения системы к одному уравнению высшего порядка.
Ответ: общее
решение системы:
 .
.
Пример
3–416:
Решить систему уравнений:
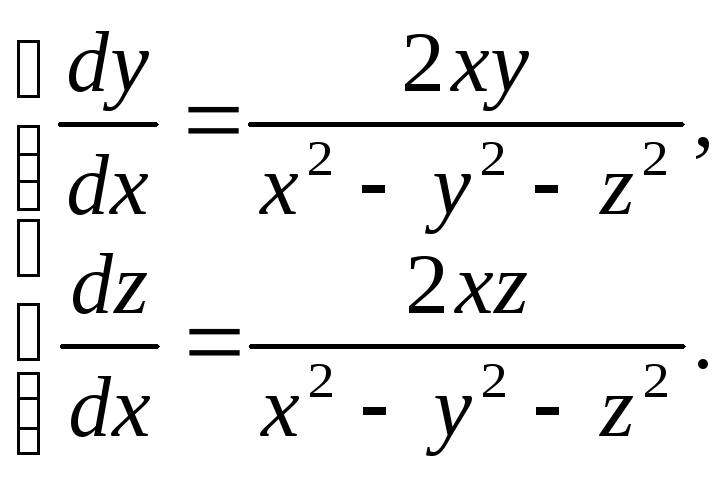 (1)
(1)
Решение:
1). Из уравнения
(1.1) получим:
![]() =
=![]() ,
аналогично из (1.2):
,
аналогично из (1.2):
![]() =
=![]() .
Эти два выражения дают:
.
Эти два выражения дают:
![]() =
=![]() →
→
![]() .
.
2). Учитывая
![]() ,
перепишем (1.1):
,
перепишем (1.1):
![]() =
=![]() →
→
![]() =
=![]() .
Или в виде:
.
Или в виде:
![]() =
=![]() – однородное уравнение в стандартной
форме. Его стандартное решение даёт:
– однородное уравнение в стандартной
форме. Его стандартное решение даёт:
![]() .
Замечание:
проверка условия:
.
Замечание:
проверка условия:
![]() здесь не нужна из-за участия произвольной
постоянной величины
здесь не нужна из-за участия произвольной
постоянной величины
![]() .
.
Ответ: общее
решение системы:
 .
.
Пример
4–418:
Решить систему уравнений:
![]() =
=![]() =
=![]() (1)
(1)
Решение:
1). Из уравнения:
![]() =
=![]() получаем:
получаем:
![]() .
Учитывая полученное выражение, запишем
уравнение:
.
Учитывая полученное выражение, запишем
уравнение:
![]() =
=![]() или:
или:
![]() =1+
=1+![]() .
.
2). Полученное
уравнение стандартным алгоритмом
приводится к уравнению с разделяющимися
переменными! Пусть:
![]() ,
вычислим производную по переменной
,
вычислим производную по переменной
![]() ,
имеем:
,
имеем:
![]() .
Тогда
.
Тогда
![]() ,
окончательно:
,
окончательно:
![]() – переменные разделились! Интегрируя
последнее, получаем выражение:
– переменные разделились! Интегрируя
последнее, получаем выражение:
![]() ,
или
,
или
![]() .
.
Ответ: общее
решение системы:
![]() ,
,
![]() .
.
Пример
5–420:
Найти общее и частное решения:
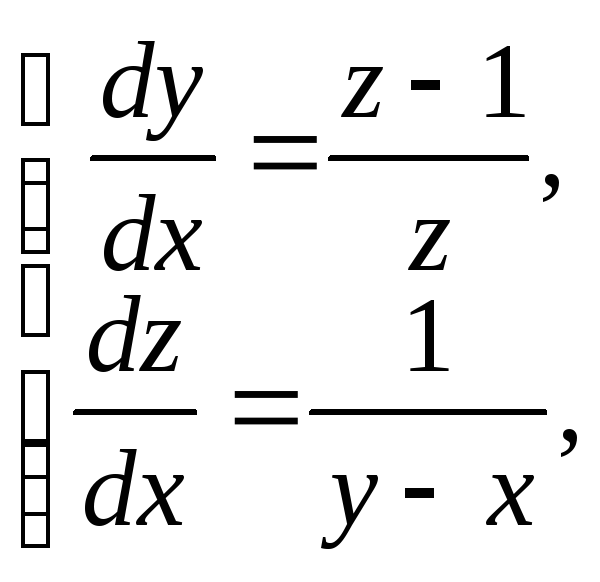
![]() ,
,
![]() . (1)
. (1)
Решение:
1). Продифференцируем
уравнение (1.2):
![]() =–
=–![]() =
=![]() .
Учитывая уравнение (1.2) получим уравнение:
.
Учитывая уравнение (1.2) получим уравнение:
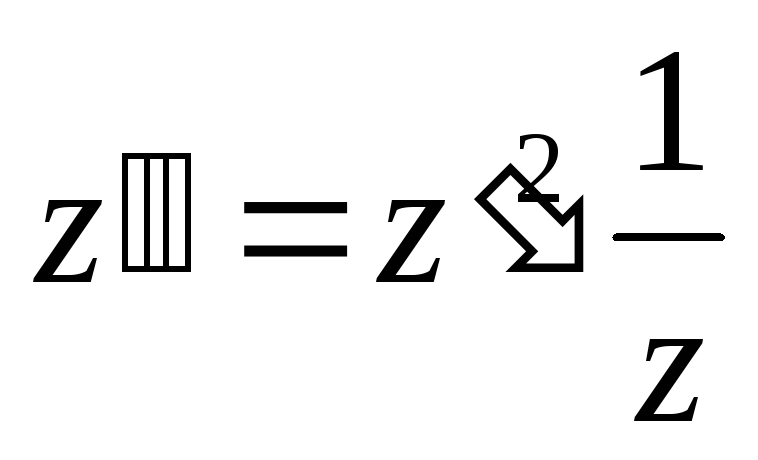 ,
которое не содержит переменной
,
которое не содержит переменной
![]() и решается понижением порядка.
и решается понижением порядка.
![]() →
→
![]() .
Тогда имеем:
.
Тогда имеем:
![]() ,
или (так как из уравнения (1.2):
,
или (так как из уравнения (1.2):
![]() )
уравнение:
)
уравнение:
![]() – уравнение с разделяющимися переменными,
откуда:
– уравнение с разделяющимися переменными,
откуда:
![]() и далее выражение:
и далее выражение:
![]() .
.
2). Дифференцируем
выражение:
![]() и используем уравнение (1.2). Полученное
выражение для функции
и используем уравнение (1.2). Полученное
выражение для функции
![]() :
:
![]() .
.
3). Общее решение
уравнения:
![]() ,
,
![]() .
.
4). Используя
заданные начальные условия, имеем:
![]() ,
,
![]() ,
откуда получаем величины
,
откуда получаем величины
![]() ,
,
![]() .
Записываем частное решение:
.
Записываем частное решение:
![]() ,
,
![]() .
.
Ответ: Частное
решение:
![]() ,
,
![]() .
.
Пример
6–422*:
Для системы уравнений:
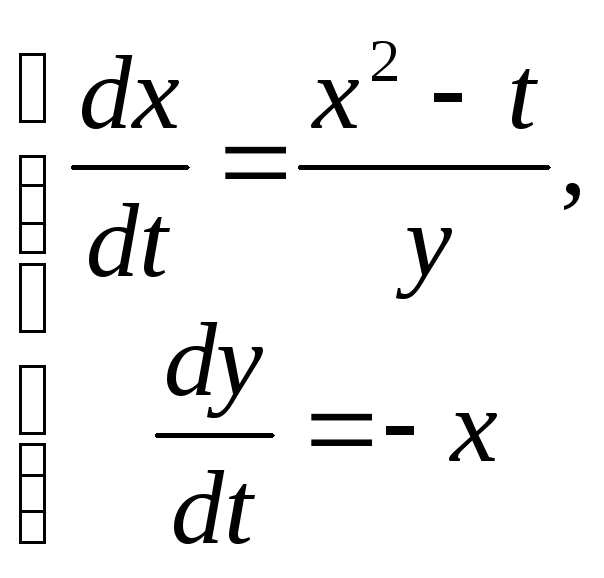 и функций
и функций
![]() и
и
![]() .
.
проверить, являются
ли соотношения
![]() первыми интегралами системы.
первыми интегралами системы.
Решение:
Замечание: ![]() является первым интегралом системы
является первым интегралом системы
![]() ,
,
![]() тогда и только тогда, когда:
тогда и только тогда, когда:
![]() .
(1)
.
(1)
1). Проверим уравнение
(1) для функции
![]() :
:
![]() – тождественно.
Является.
– тождественно.
Является.
2). Проверим уравнение
(1) для функции
![]() :
:
![]() .
Не является.
.
Не является.
Ответ: соотношение
![]() –
является, а соотношение
–
является, а соотношение
![]() –
не является.
–
не является.
Пример
7–427:
Решить систему уравнений:
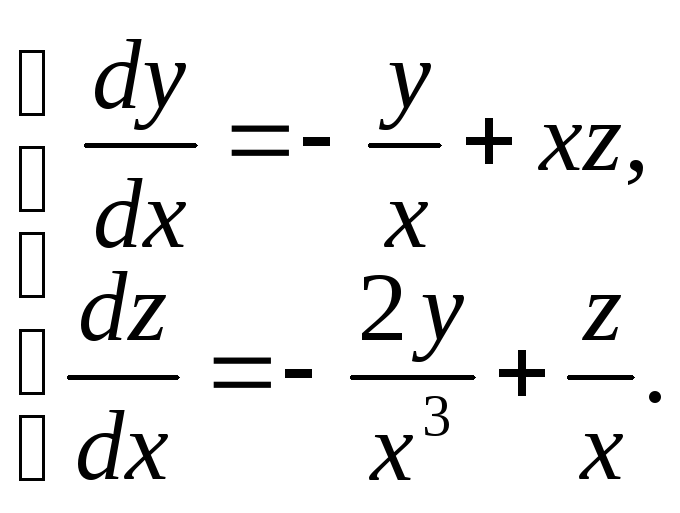 (1).
(1).
Решение:
1). Перепишем
уравнение (1.1):
![]() →
→
![]() .
Для дальнейшего использования уравнение
(1.2) запишем в виде:
.
Для дальнейшего использования уравнение
(1.2) запишем в виде:
![]() .
.
2). Продифференцируем
уравнение (1.1):
![]() .
Учитывая выражения для функции
.
Учитывая выражения для функции
![]() и для произведения
и для произведения
![]() ,
получим уравнение
,
получим уравнение
![]() ,
которое после умножения на
,
которое после умножения на
![]() .
принимает вид:
.
принимает вид: ![]() – уравнение Эйлера. (2)
– уравнение Эйлера. (2)
3). Применим
подстановку:
![]() .
Вычисляя производные
.
Вычисляя производные
![]() ,
,
![]() и учитывая уравнение (2), получаем
уравнение:
и учитывая уравнение (2), получаем
уравнение:
![]() .
Его корни:
.
Его корни:
![]() =
=![]() ,
,
![]() =
=![]() .
.
4). Записываем ФСР:
![]() =
=![]() и
и
![]() =
=![]() .
Общее решение:
.
Общее решение:
![]() =
=![]() .
.
5). Вычислим
производную:
![]() .
Учитывая полученное ранее выражение
.
Учитывая полученное ранее выражение
![]() ,
получаем:
,
получаем:
![]() =
=![]() .
.
Ответ: общее
решение системы
![]() =
=![]() ;
;
![]() =
=![]() .
.
Замечание: обратим внимание на особенности применения способа решения системы ДУ сведением к уравнению высшего порядка для одной из искомых функций: здесь интенсивное применение средств математического анализа сочетается с достаточно тонкими средствами школьной алгебры!..
☺☺
Общие
сведения. Учитывая, что трудоёмкость
решения систем дифференциальных
уравнений существенно зависит от числа
функций, участвующих в построении
системы, в предлагаемых для самостоятельных
упражнений заданиях мы ограничиваемся
системами, состоящими из двух уравнений.
Поэтому все общие выражения, применяемые
при решении систем уравнений, относим
только к системам двух дифференциальных
уравнений:
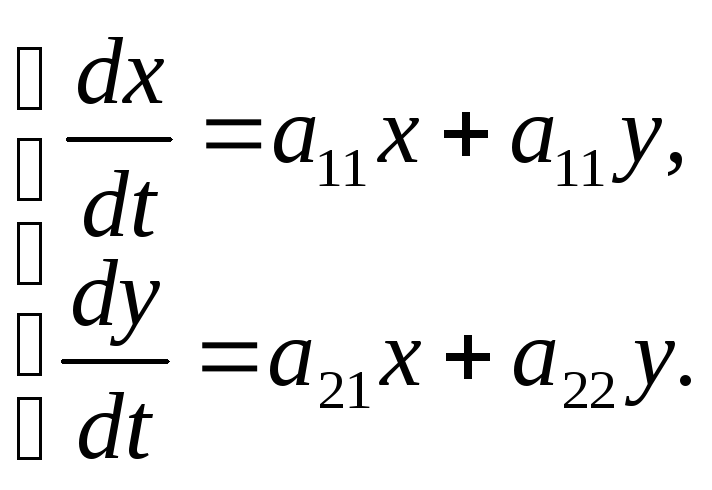 (1)
(1)
где
![]() –
действительные числа (постоянные);
–
действительные числа (постоянные);
![]() ,
,![]() – искомые, дифференцируемые функции.
– искомые, дифференцируемые функции.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
☻
Вопросы для самопроверки:
-
Что такое «нормальная форма» записи системы уравнений 1-го порядка?
-
Как уравнение n-го порядка представить в виде системы уравнений 1-го порядка?
-
Как систему уравнений 1-го порядка сводят к одному уравнению n -го порядка?
-
Как записывают начальные условия для системы трёх уравнений 1-го порядка?
☺☺
Общие
сведения. Учитывая, что трудоёмкость
решения систем дифференциальных
уравнений существенно зависит от числа
функций, участвующих в построении
системы, в предлагаемых для самостоятельных
упражнений заданиях мы ограничиваемся
системами, состоящими из двух уравнений.
Поэтому все общие выражения, применяемые
при решении систем уравнений, относим
только к системам двух дифференциальных
уравнений:
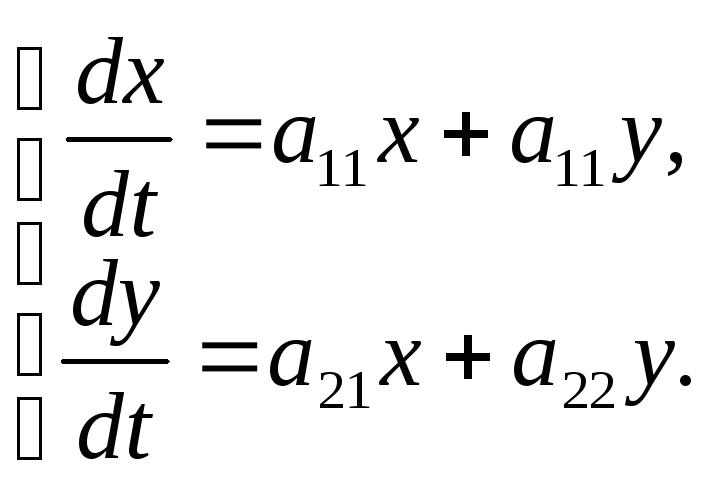 (1)
(1)
где
![]() –
действительные числа (постоянные);
–
действительные числа (постоянные);
![]() ,
,![]() – искомые, дифференцируемые функции.
– искомые, дифференцируемые функции.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
Решение системы
уравнений подсказывает равносильность
системы (1) линейному дифференциальному
уравнению 2-го порядка с постоянными
коэффициентами для любой из функций
![]() ,
,![]() ,
а также свойство производной функции
,
а также свойство производной функции
![]() :
при дифференцировании вид функции не
меняется. Так как в системе уравнений
участие функций
:
при дифференцировании вид функции не
меняется. Так как в системе уравнений
участие функций
![]() ,
,![]() согласовывается
при помощи коэффициентов
согласовывается
при помощи коэффициентов
![]() ,
то, нетрудно догадаться, что решение
системы следует искать в виде:
,
то, нетрудно догадаться, что решение
системы следует искать в виде: ![]() ,
,
![]() , (2)
, (2)
причем коэффициенты
![]() ,
,
![]() =1,2
– будут определяться из условия, что
совокупность функций в записи (2) есть
решение системы уравнений (1):
=1,2
– будут определяться из условия, что
совокупность функций в записи (2) есть
решение системы уравнений (1):
 или
или
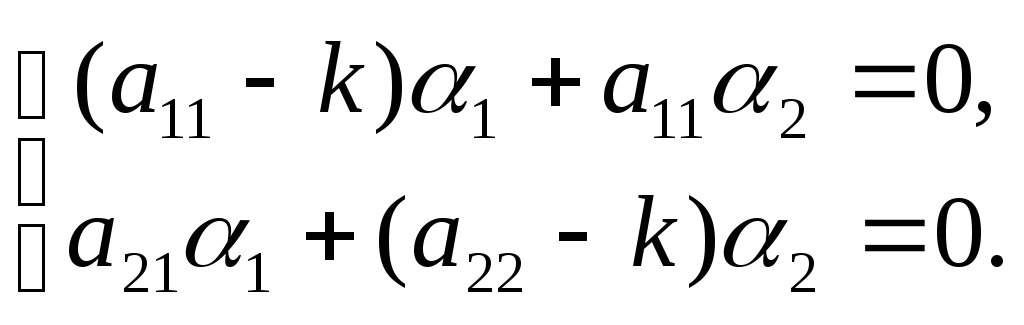 (3)
(3)
Замечание:
система уравнений (3) записана с учётом
деления каждого из уравнений на общий
множитель:
![]() .
.
Известно, система линейных однородных (алгебраических) уравнений имеет ненулевые решения только в случае, если её определитель равен нулю:
![]() =
=![]() =0. (4)
=0. (4)
Уравнение-многочлен
![]() =0
называется характеристическим
для системы (1), его корни – характеристическими
корнями этой системы.
=0
называется характеристическим
для системы (1), его корни – характеристическими
корнями этой системы.
Дальнейшее использование полученных характеристических корней зависит от их вида. Различают случаи:
Случай-1.
Корни уравнения ∆(k)
= 0 действительные и различные:
![]() ,
,![]() .
.
Для каждого
![]() из системы (3) определится набор
коэффициентов:
из системы (3) определится набор
коэффициентов:
![]() ,
,![]() ,
,![]() =1,2,
что определит полный набор решений
системы (1):
=1,2,
что определит полный набор решений
системы (1):
![]() =
=![]() ·
·![]() ,
,
![]() =
=![]() ·
·![]() ,
(5)
,
(5)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
![]() =
=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() +
+![]() ·
·![]() ·
·![]() , (6)
, (6)
где
![]() ,
,![]() - произвольные постоянные. Запись (6)
называют общим
решением
системы уравнений (1).
- произвольные постоянные. Запись (6)
называют общим
решением
системы уравнений (1).
Если
заданы начальные условия:
![]() =
=![]() ,
,![]() =
=![]() ,
можно определить такие значения
,
можно определить такие значения
![]() ,
,![]() ,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
![]() .
.
Случай-2.
Корни уравнения ∆(k)
= 0 комплексные:
![]() =
=![]() .
.
Для пары корней
![]() из системы (3) определятся:
из системы (3) определятся:
![]() =
=![]()
![]() i
i![]() ;
;![]() =
=![]()
![]() i
i![]() .
Применим сначала знак
.
Применим сначала знак
![]() ,
запишем решение системы (1):
,
запишем решение системы (1):
![]() =
=![]() ·
·![]() =
=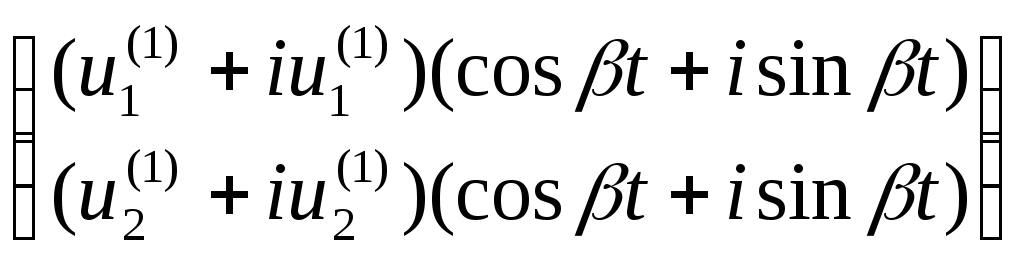 ·
·![]() , (7)
, (7)
после выполнения операций умножения комплексных чисел и несложных тождественных преобразований в выражении (7) получим:
![]() =
= ·
·![]() =
=![]() ·
·![]() +
+![]()
![]() ·
·![]() . (8)
. (8)
Аналогично, применяя
знак
![]() ,
получаем решение системы (1) с теми же
величинами, но только со знаком
,
получаем решение системы (1) с теми же
величинами, но только со знаком
![]() перед мнимой единицей
перед мнимой единицей
![]() :
:
![]() =
=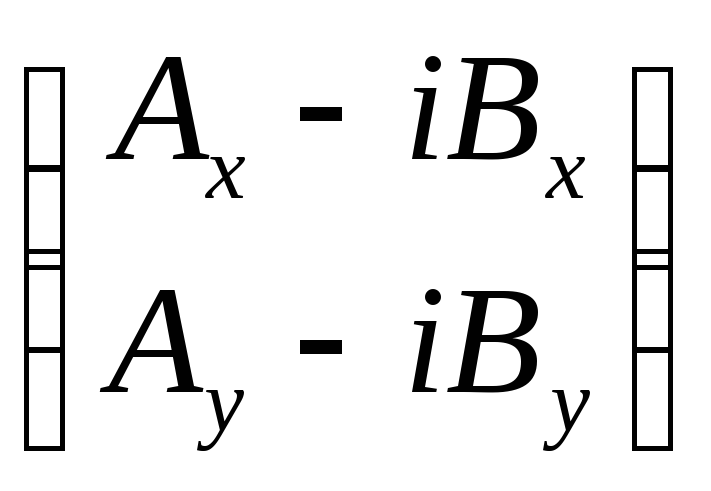 ·
·![]() =
=![]() ·
·![]() –
–![]()
![]() ·
·![]() . (9)
. (9)
Известно (была доказана теорема!), что от записей решений системы (1) с использованием выражений (8) и (9) можно перейти к записям:
![]() =
=![]() ·
·![]() и
и ![]() =
=![]() ·
·![]() . (10)
. (10)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
![]() =
=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() ·
·![]() ·
·![]() +
+![]() ·
·![]() ·
·![]() , (11)
, (11)
где
![]() ,
,![]() - произвольные постоянные. Запись (11)
называют общим решением
системы уравнений (1) для пары
характеристических корней
- произвольные постоянные. Запись (11)
называют общим решением
системы уравнений (1) для пары
характеристических корней
![]() .
.
Если заданы
начальные условия:
![]() =
=![]() ,
,![]() =
=![]() ,
можно определить такие значения
,
можно определить такие значения
![]() ,
,![]() ,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
![]() .
.
Случай-3.
Корни уравнения ∆(k)
= 0 действительные и равные:
![]() =
=![]() =
=![]() .
.
Для каждого
![]() из системы (3) определится набор
коэффициентов:
из системы (3) определится набор
коэффициентов:
![]() =
=![]() и
и
![]() =
=![]() .
Это значит, что необходимо как-то учесть
равенство (кратность) характеристических
корней. В отличие от способа учёта
кратных корней при решении уравнений
высшего порядка для одной функции, в
случае системы уравнений ищут сразу
пару решений, используя
конструкцию:
.
Это значит, что необходимо как-то учесть
равенство (кратность) характеристических
корней. В отличие от способа учёта
кратных корней при решении уравнений
высшего порядка для одной функции, в
случае системы уравнений ищут сразу
пару решений, используя
конструкцию: ![]() =
=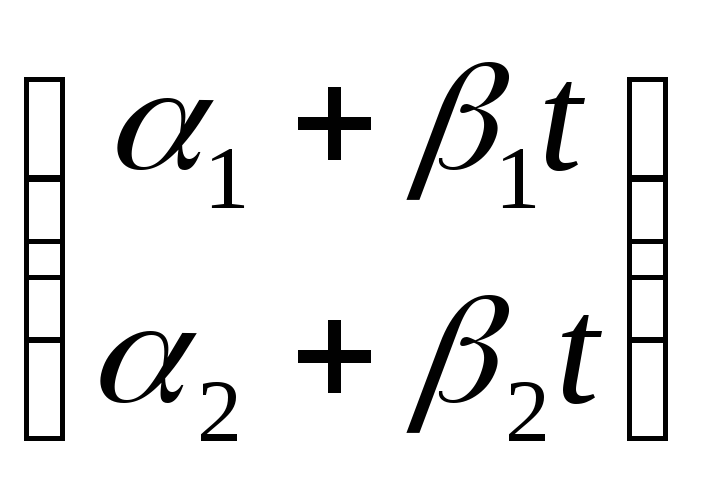 ·
·![]() ,
(12)
,
(12)
Так как выражение
(12) должно быть решением, то необходимо
участвующие параметры подчинить
заданной системе уравнений (1). Подставим
(12) в систему (1), сократив на число
![]() ,
получим систему тождеств:
,
получим систему тождеств:
 (13)
(13)
Приравнивая в
тождествах (13) коэффициенты при одинаковых
степенях
![]() ,
получаем системы уравнений: при
,
получаем системы уравнений: при
![]() :
: 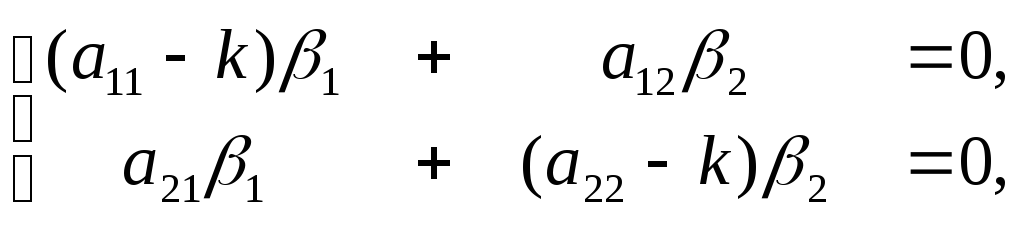 (14)
(14)
при
![]() :
: 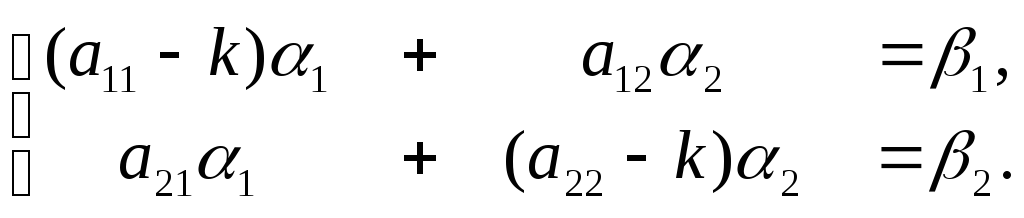 (15)
(15)
Порядок нахождения
параметров
![]() ,
,![]() =1,2
из систем уравнений (14) и (15):
=1,2
из систем уравнений (14) и (15):
1). Из системы (14)
находим параметры
![]() :
так как определитель системы равен 0,
то ненулевые решения у системы найдутся.
Принимая свободную неизвестную
:
так как определитель системы равен 0,
то ненулевые решения у системы найдутся.
Принимая свободную неизвестную
![]() =
=![]() ,
получим в выражении (12) участие свободной
неизвестной. Параметр
,
получим в выражении (12) участие свободной
неизвестной. Параметр
![]() будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего решения системы!
будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего решения системы!
2). Используя
найденные параметры
![]() ,
решаем систему уравнений (15). Это система
также имеет ненулевые решения:
,
решаем систему уравнений (15). Это система
также имеет ненулевые решения:
![]() .
Принимая свободную неизвестную
.
Принимая свободную неизвестную
![]() =
=![]() ,
получим в выражении (12) участие ещё одной
свободной неизвестной. Параметр
,
получим в выражении (12) участие ещё одной
свободной неизвестной. Параметр
![]() будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего
решения системы!
будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего
решения системы!
Итак, получено общее решение системы дифференциальных уравнений (1) для случая кратных действительных корней.
Если
заданы начальные условия:
![]() =
=![]() ,
,![]() =
=![]() ,
можно определить такие значения
,
можно определить такие значения
![]() ,
,![]() ,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
![]() .
.
••• ≡ •••
Пример
1–431:
Решить
систему линейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни системы:
![]() =
=
![]() = 0, откуда получаем:
= 0, откуда получаем:
![]() =1,
=1,
![]() =2.
Для каждого
=2.
Для каждого
![]() определится набор коэффициентов:
определится набор коэффициентов:
![]() ,
,
![]() ,
что определит полный набор решений
заданной системы:
,
что определит полный набор решений
заданной системы:
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() . (1.1)
. (1.1)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
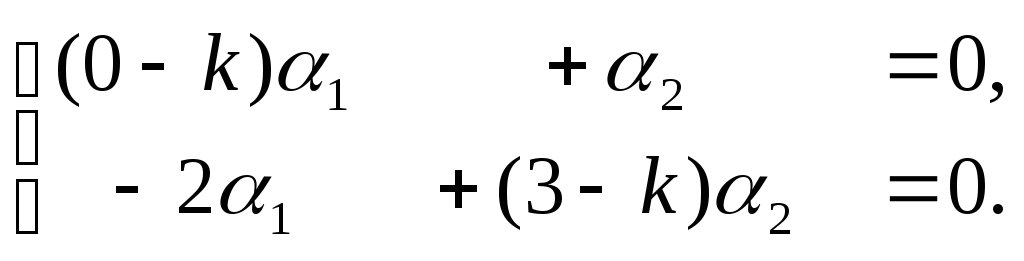 (2.1)
(2.1)
3).
Для
корня
![]() =1
система (2.1) имеет решение
=1
система (2.1) имеет решение
![]() =
=![]() ;
для
;
для
![]() =2
система (2.1) имеет решение:
=2
система (2.1) имеет решение:
![]() =
=![]() .
.
Замечание: решение системы (2.1) проводится по известным правилам из курса «Линейная алгебра».
4). С учетом полученных
векторов
![]() ,
,
![]() составим общее решение исходной системы
дифференциальных уравнений:
составим общее решение исходной системы
дифференциальных уравнений:
![]() =1,
=1,
![]() =0
=0
![]() =
=![]()
![]() +
+![]()
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() .
(3.1)
.
(3.1)
Ответ:
общее решение системы:
![]() =
=![]()
![]() +
+![]()
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() .
.
Пример
2–432:
Решить систему уравнений:
![]() при условии:
при условии:
![]() .
.
Решение:
1). Найдем
характеристические корни системы:
![]() =
=
![]() = 0, откуда получаем:
= 0, откуда получаем:
![]() =2,
=2,
![]() =4.
Для каждого
=4.
Для каждого
![]() определится набор коэффициентов:
определится набор коэффициентов:
![]() ,
,
![]() ,
что определит полный набор решений
системы (1):
,
что определит полный набор решений
системы (1):
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() , (1)
, (1)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
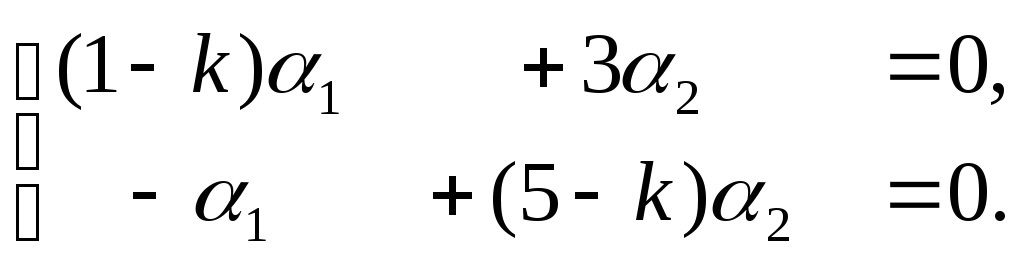 (2)
(2)
3).
Для
корня
![]() система (2) имеет решение
система (2) имеет решение
![]() =
=![]() ;
для корня
;
для корня
![]() система (2) имеет решение:
система (2) имеет решение:
![]() =
=![]() .
.
4). С учетом полученных
векторов
![]() ,
,
![]() составим общее решение исходной системы
дифференциальных уравнений:
составим общее решение исходной системы
дифференциальных уравнений: ![]() =
=![]()
![]() +
+![]()
![]() =
=![]()
![]() ∙e2t
+
∙e2t
+![]()
![]() ∙e4t.
(3)
∙e4t.
(3)
5). Учитывая начальные условия и запись общего решения, получим:
![]() =
=![]()
![]() +
+![]()
![]() ,
откуда
,
откуда
![]() =1,
=1,
![]() =0. (4)
=0. (4)
6). Используя
результаты (4), запишем частное решение
системы, удовлетворяющее начальным
условиям: ![]() =
=![]() ∙e2t. (5)
∙e2t. (5)
Ответ:
Общее решение системы:
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() ,
частное:
,
частное:
![]() =
=![]() ∙
∙![]() .
.
Пример
3–438:
Найти частное решение системы:
 если:
если:
![]() .
.
Решение:
1). Найдем
характеристические корни системы:
![]() =
=
 = 0, откуда получаем:
= 0, откуда получаем:
![]() =
=![]() =–1;
=–1;
![]() =2.
В этом случае решение системы для
кратного корня
=2.
В этом случае решение системы для
кратного корня
![]() =–1
необходимо искать в виде:
=–1
необходимо искать в виде:  , (1.4)
, (1.4)
2). Подставим (1) исходную систему уравнений:
 (2.4)
(2.4)
3). Так как в системе
уравнений (2.4) каждое уравнение является
тождеством, то все неизвестные коэффициенты
найдем, приравнивая коэффициенты при
одинаковых степенях:
![]() и
и
![]() :
:
при
![]() :
:  откуда получаем:
откуда получаем:
![]() ; (3.4)
; (3.4)
при
![]() :
: 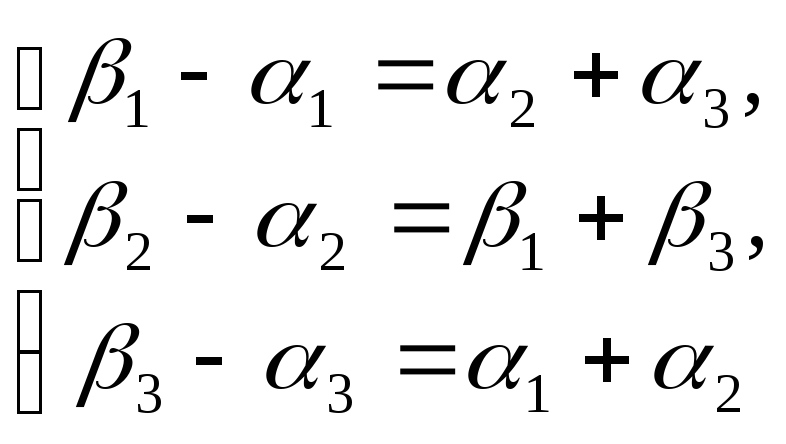 получаем:
получаем:
![]() =
=
![]() . (4.4)
. (4.4)
В данной задаче,
если в уравнении (3.4) принять в качестве
свободных неизвестных две из неизвестных
![]() ,
то из (4.4) получается
,
то из (4.4) получается
![]() ,
то есть неизвестные не могут быть
свободными в общей системе (3.4),(4.4). Тогда
из (4.4):
,
то есть неизвестные не могут быть
свободными в общей системе (3.4),(4.4). Тогда
из (4.4):
![]() получаем значения остальных параметров:
получаем значения остальных параметров:
![]() ,
,![]() ,
,
![]() .
.
4). Учитывая
полученные в (3) значения коэффициентов,
можно представить запись (1) в виде: 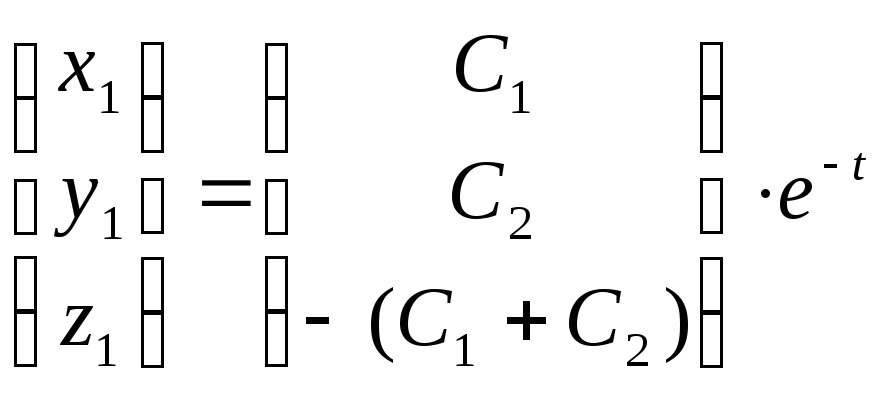 ,
(5.4)
,
(5.4)
5). Для определения
вектора
![]() составим систему уравнений:
составим систему уравнений:
 (6.4)
(6.4)
6). Для корня
![]() из системы (5) имеем:
из системы (5) имеем:
![]() =
=![]() ,
тогда:
,
тогда:
![]() =
=![]() ∙
∙![]() ∙
∙![]() . (7.4)
. (7.4)
7). С учетом полученных решений (4.6) и (6.6), составим общее решение исходной системы дифференциальных уравнений (с учетом свойств матриц):
![]() =
=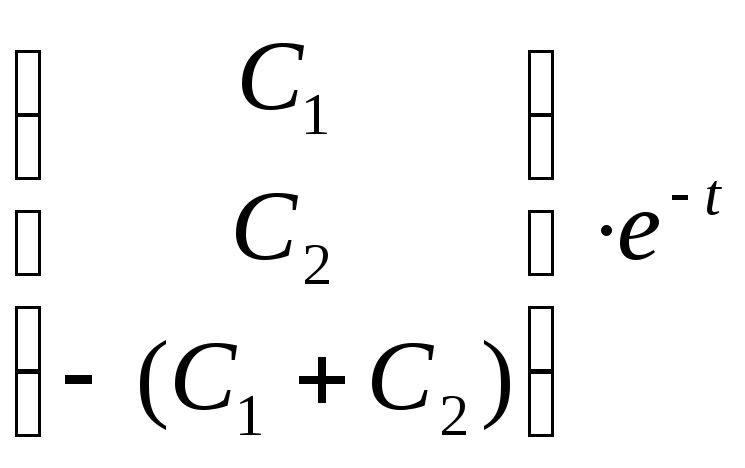 +
+![]() ∙
∙![]() ∙
∙![]() . (8.4)
. (8.4)
8). Учитывая начальные условия и запись общего решения, получим:
![]() =
=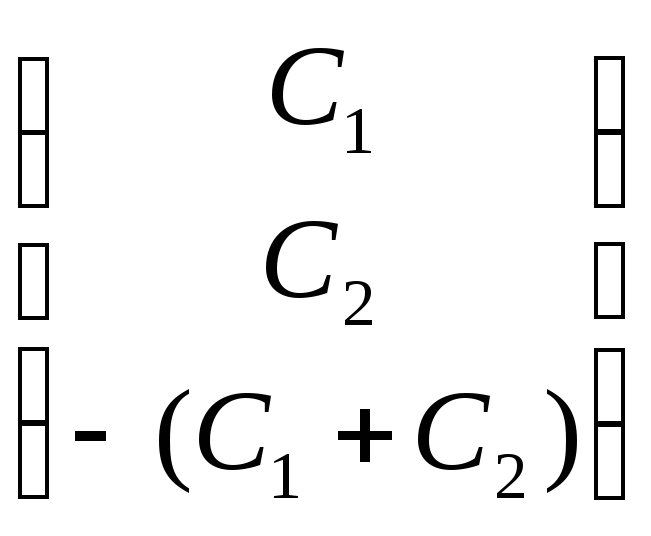 +
+![]() ∙
∙![]() ,
откуда
,
откуда
![]() =1,
=1,
![]() =1,
=1,
![]() =1. (9.4)
=1. (9.4)
9). Используя
результаты (8.6), запишем частное решение
системы, удовлетворяющее начальным
условиям: ![]() =
=![]() ∙
∙![]() +
+
![]() ∙
∙![]() . (10.4)
. (10.4)
Ответ: частное
решение системы:
![]() =
=![]() ∙
∙![]() +
+![]() ∙
∙![]() .
.
Пример
4–440:
Решить систему уравнений:

Решение:
1). Найдем
характеристические корни системы:
![]() =
=
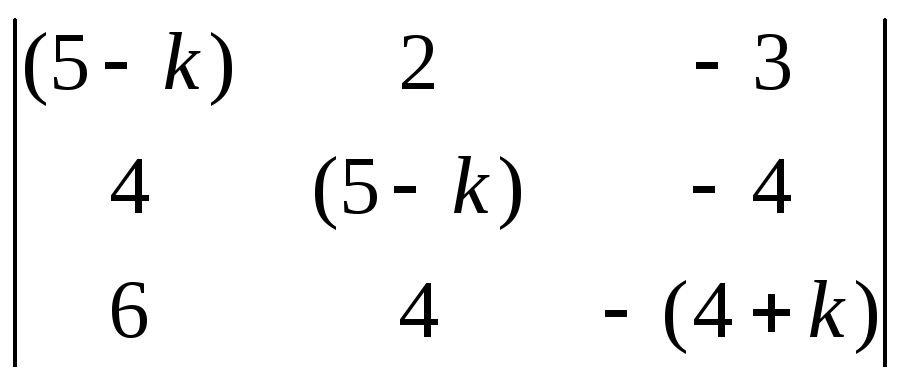 = 0, откуда получаем:
= 0, откуда получаем:
![]() =1,
=1,![]() =2;
=2;
![]() =3.
=3.
Замечание:
решение уравнения
![]() =
=![]() =0
проводится по Виету: угадали все корни
как множители числа 6.
=0
проводится по Виету: угадали все корни
как множители числа 6.
2). Для каждого
![]() определится набор коэффициентов:
определится набор коэффициентов:
![]() ,
,
![]() ,
,![]() ,
что определит полный набор решений
системы (1):
,
что определит полный набор решений
системы (1):
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
, ![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
(1.5)
,
(1.5)
3). Для определения
векторов
![]() ,
,![]() ,
,![]() составим систему уравнений:
составим систему уравнений:
 (2.5)
(2.5)
4).
Для
значения
![]() система (2.5) имеет решение:
система (2.5) имеет решение:
![]() =
=![]() ,
для значения
,
для значения
![]() система (2.5) имеет решение:
система (2.5) имеет решение:
![]() =
=![]() ,
для значения
,
для значения
![]() система (2.5) имеет решение:
система (2.5) имеет решение:
![]() =
=![]() .
.
5). С учетом полученных
векторов
![]() ,
,![]() ,
,![]() составим общее решение исходной системы
дифференциальных уравнений:
составим общее решение исходной системы
дифференциальных уравнений:
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() .
(3.5)
.
(3.5)
Ответ:
Общее решение системы:
![]() =
=![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() +
+![]()
![]() ∙
∙![]() .
.
☺☺
Пример
5–444:
Решить
систему нелинейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функций
![]() =
=![]() и
и
![]() =
=![]() ):
∆(k)=
):
∆(k)=![]() =0,
откуда получаем:
=0,
откуда получаем:
![]() =
=![]() ,
,
![]() =
=![]() .
В этом случае общее решение однородной
системы будем искать в виде:
.
В этом случае общее решение однородной
системы будем искать в виде:
![]() =
=![]()
![]() +
+![]()
![]() ,
(1)
,
(1)
где
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() , (2)
, (2)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
 (3)
(3)
3). Для значения
![]() =
=![]() =
=![]() система (3) имеет решение:
система (3) имеет решение:
![]() =
=![]() .
Тогда можно записать:
.
Тогда можно записать:
![]() =
=![]() ∙
∙![]() =
=![]() =
= . (4)
. (4)
4). Для значения
![]() =
=![]() =
=![]() система (3) имеет решение:
система (3) имеет решение:
![]() =
=![]() .
Аналогично получаем:
.
Аналогично получаем:
![]() =
=![]() ∙
∙![]() =
=![]() =
=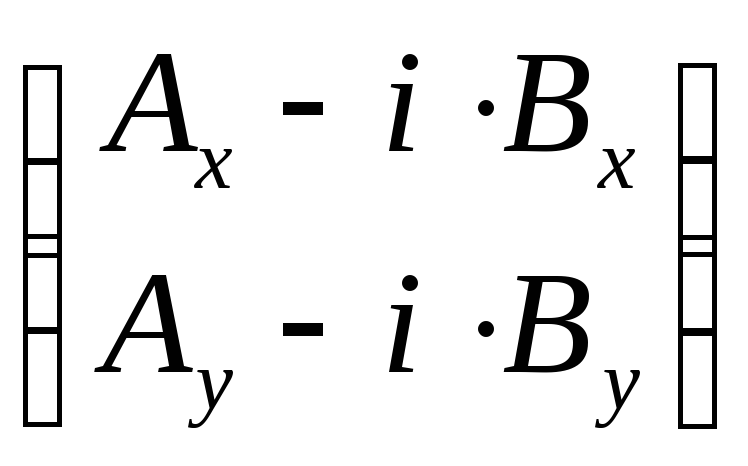 , (5)
, (5)
то есть решения
![]() и
и
![]() (выражения (4)и (5)) комплексно-сопряженные.
(выражения (4)и (5)) комплексно-сопряженные.
5). В качестве
частных решений системы уравнений берем
отдельно мнимую и действительную части.
Получаем: ![]() =
=![]() ,
, ![]() =
=![]() . (6)
. (6)
6). С учетом выражений
(6) запишем общее решение однородной
системы дифференциальных уравнений:
![]() =
=![]()
![]() +
+![]()
![]() .
(7)
.
(7)
7). Так как функции:
![]() =
=![]() и
и
![]() =
=![]() – имеют специальный вид и общее образующее
число
– имеют специальный вид и общее образующее
число
![]() ,
причем совпадает с характеристическими
корнями
,
причем совпадает с характеристическими
корнями
![]() и
и
![]() ,
то частное решение заданной системы
будем искать в виде:
,
то частное решение заданной системы
будем искать в виде:
![]() =
=![]() .
(8)
.
(8)
8). Подставляя (8) в заданную систему, получаем систему тождеств:
![]() =
=
=![]() , (9)
, (9)
![]() =
=
=![]() .
.
Приравнивая
коэффициенты при подобных членах
тождеств (9), получим алгебраическую
систему уравнений, решением которой
является:
![]() =–1,
=–1,
![]() =
=![]() =
=![]() =
=![]() =
=![]() =0,
=0,
![]() =
=![]() =1.
Тогда (8) можно записать в виде:
=1.
Тогда (8) можно записать в виде:
![]() =
=![]() (10)
(10)
9). Запишем общее решение заданной неоднородной системы:
![]() =
=![]() +
+![]() =
=
 ∙
∙![]() .
(11)
.
(11)
Ответ:
Общее решение:
![]() =
=
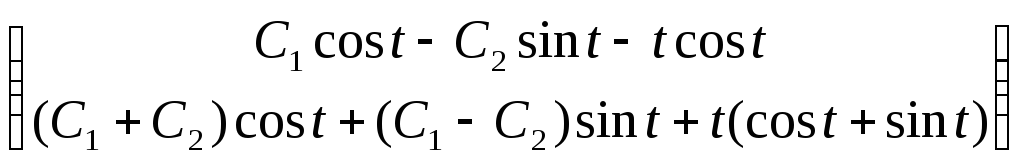 ∙
∙![]() .
.
Вопросы для самопроверки:
-
Как по записи системы уравнений 1-го порядка определить, что она линейная?
-
Почему линейная система однородных уравнений с постоянными коэффициентами удовлетворяет требованиям теоремы «о существовании и единственности решений»?
-
Как записывают характеристический многочлен для системы линейных однородных уравнений с постоянными коэффициентами?
-
Как записывают общее решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как находят частное решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как учитывают кратность характеристических корней при решении системы линейных однородных уравнений с постоянными коэффициентами?
☺☺
