
- •Практикум по линейной алгебре Задачи и упражнения к главе 1. Матрицы и действия над ними. Определитель квадратной матрицы
- •1). . 2).. 3)..
- •10). .
- •1.3. A) ; б) ; в).
- •Задачи и упражнения к главе 2. Элементарные преобразования матриц
- •2.1. Решения.
- •2.16. А).
- •2.17. А). Решение.
- •Задачи и упражнения к главе 3. Решение систем линейных уравнений
- •1) 2)3)
- •4) 5)6)
- •7) 8)9)
- •10) 11)12)
- •Глава 1. Матрицы и действия над ними. Определитель квадратной матрицы
Задачи и упражнения к главе 2. Элементарные преобразования матриц
Краткие теоретические сведения. Сложение, вычитание и умножение строк и столбцов осуществляется поэлеметно:
![]()
![]()
![]()
Строка
![]() называется нулевой.
называется нулевой.
Элементарные преобразования строк матрицы:
I-го типа: перестановка двух строк местами.
II-го типа: прибавление
![]() -ой
строке матрицы её
-ой
строке матрицы её![]() -ой
строки, умноженной на число (запись
-ой
строки, умноженной на число (запись![]() );
);
III-го типа: умножение
![]() -ой
строки на ненулевое число (запись
-ой
строки на ненулевое число (запись![]() );
);
Первое ненулевое число строки назовем
её лидером. Лидеры строк матрицы
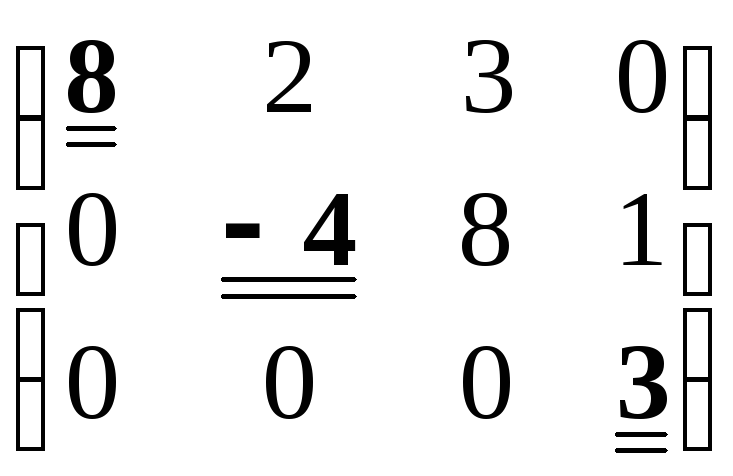 подчеркнуты. Лидер третьей строки
расположен в 4-ом столбце.
подчеркнуты. Лидер третьей строки
расположен в 4-ом столбце.
Матрицу называют ступенчатой, если
1) нулевые строки расположены ниже всех остальных;
для каждой ненулевой строки
2) лидер следующей строки расположен правее лидера данной строки. "Правее" означает в столбце с большим номером.
Всякую матрицу конечным числом элементарных преобразований строк можно превратить в ступенчатую матрицу.
В простейшем случае схема приведения матрицы к ступенчатой форме с помощью элементарных преобразований строк имеет следующий вид:
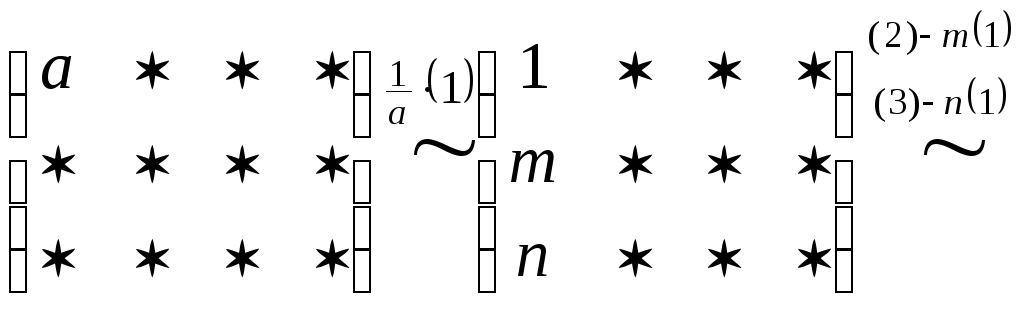
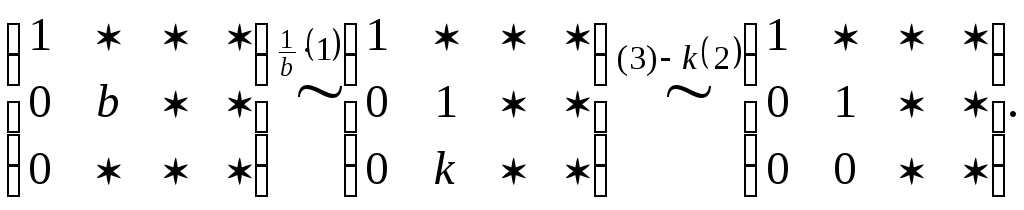
2.1. При помощи элементарных
преобразований строк преобразовать
матрицу сначала к ступенчатому виду, а затем к
приведённому ступенчатому виду.
сначала к ступенчатому виду, а затем к
приведённому ступенчатому виду.
2.2. Приведите матрицу к ступенчатому виду с помощью элементарных преобразований строк:
1)
 2)
2)

3)
 4)
4)
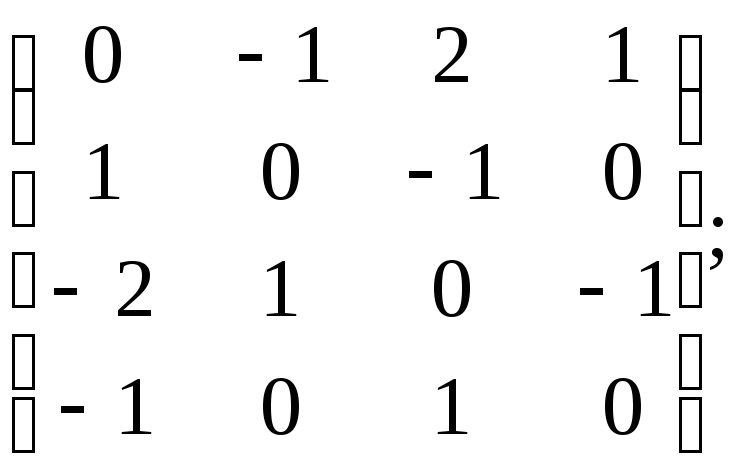
5)
 6)
6)

7)
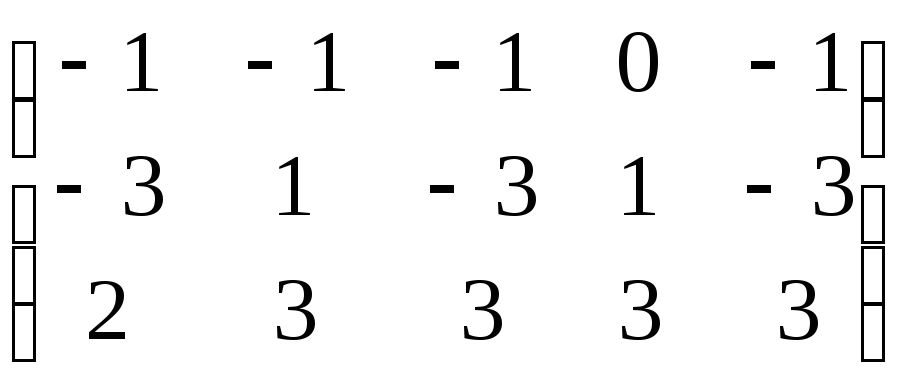 ;
8)
;
8)
 .
.
2.3. Элементарными преобразованиями строк приведите матрицы из предыдущей задачи к приведённому ступенчатому виду.
2.4. Используя элементарные
преобразования строк и столбцов привести
определитель к ступенчатому виду и
вычислить его:
2.5. Используя пропорции докажите,
что следующие четыре условия на матрицу
![]() размера
размера
![]() равносильны:
равносильны:
1)
![]()
![]()
2) существуют ненулевой столбец ненулевая
строка (![]() )
такие, что
)
такие, что
![]()
![]() (
(![]() )
)
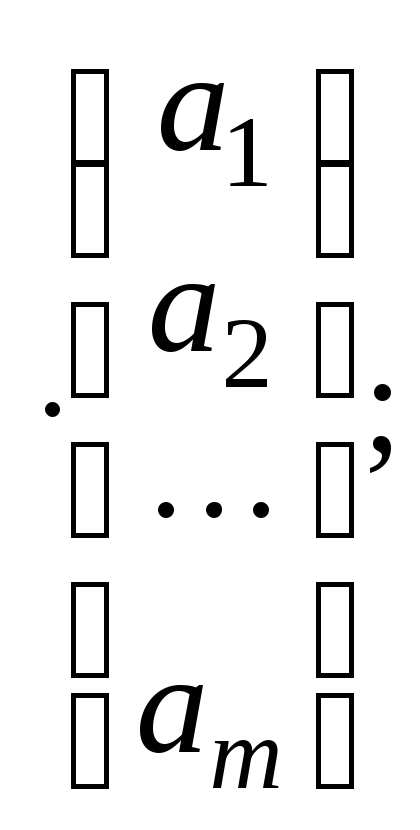
3) все строки матрицы
![]() пропорциональны друг другу;
пропорциональны друг другу;
4) все столбцы матрицы
![]() пропорциональны друг другу.
пропорциональны друг другу.
2.6. Найти ранг матрицы:
а)
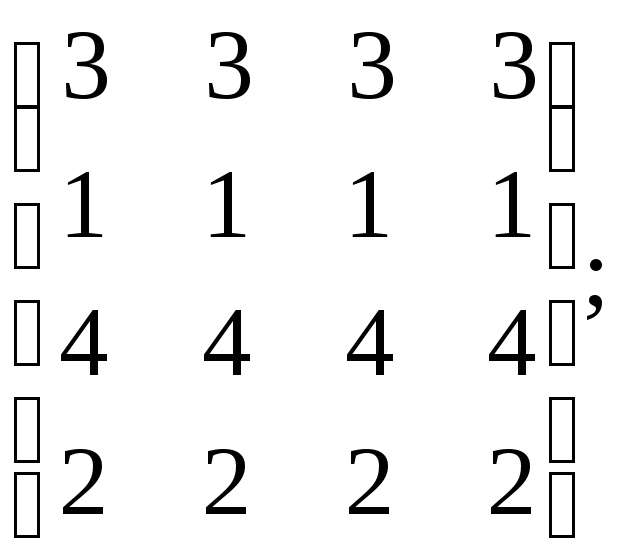 б)
б)
 в)
в)
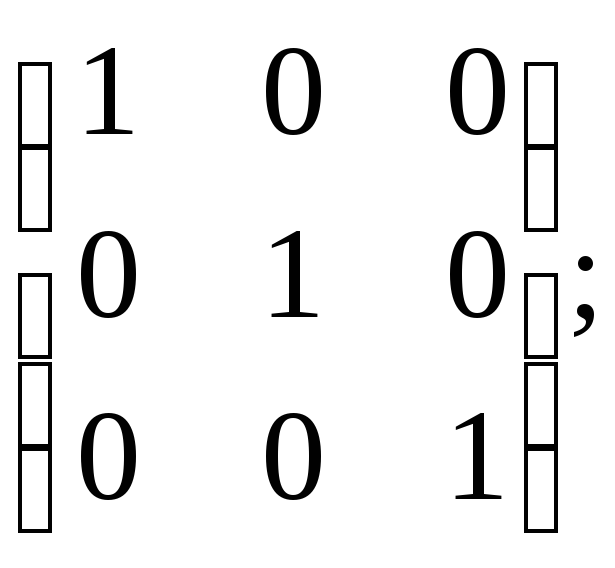 г)
г)
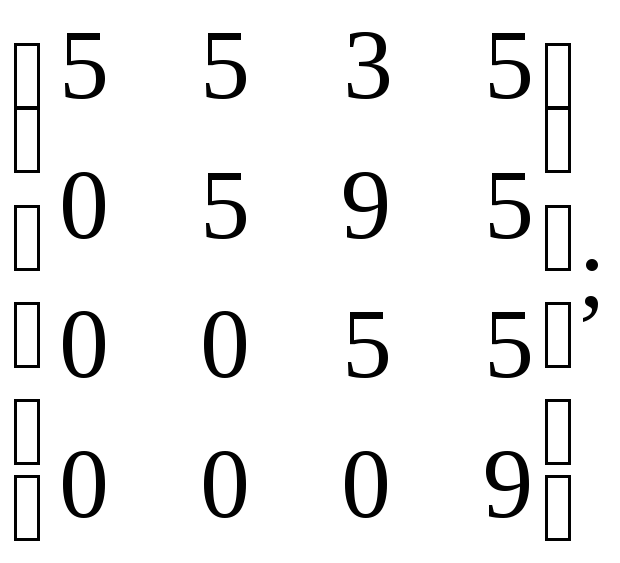
д)
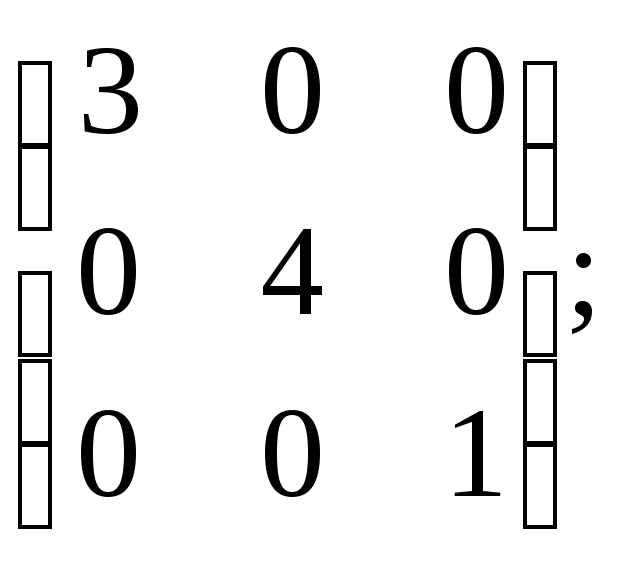 е)
е)
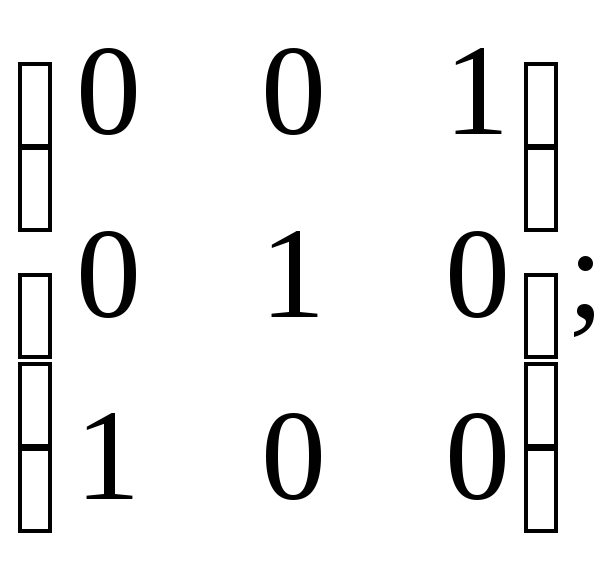 ж)
ж)

з)
 и)
и)
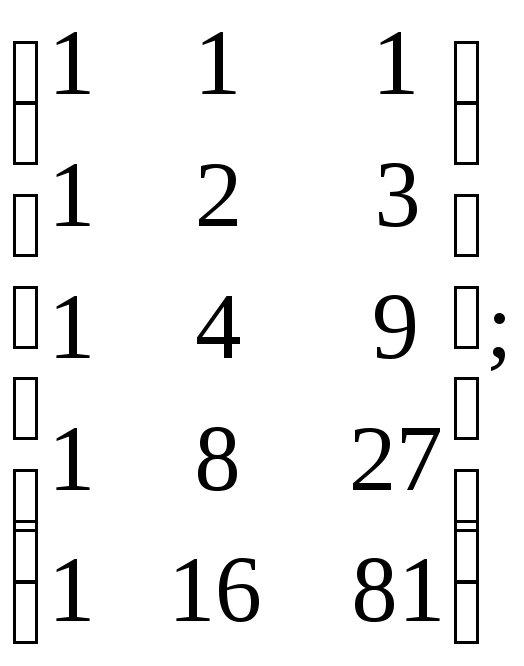 к)
к)
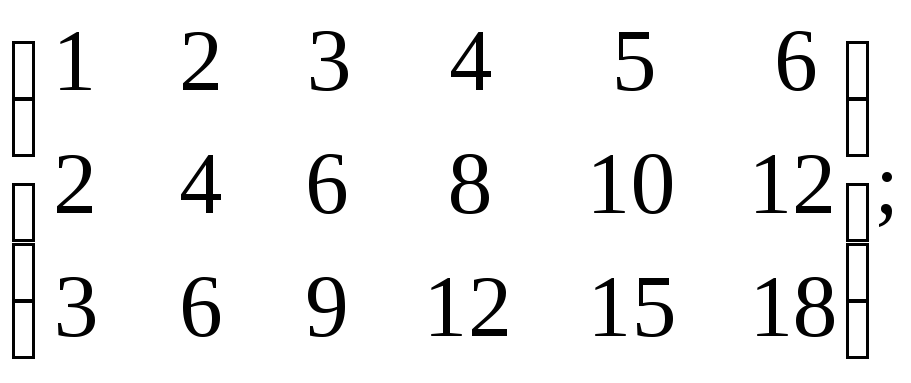
л)
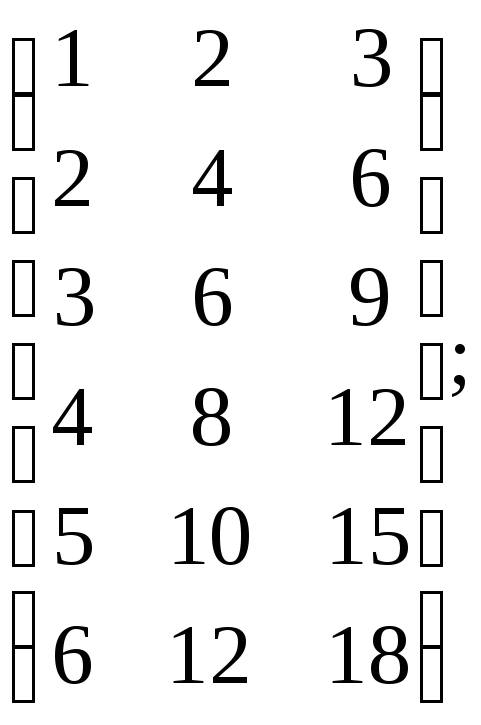 м)
м)
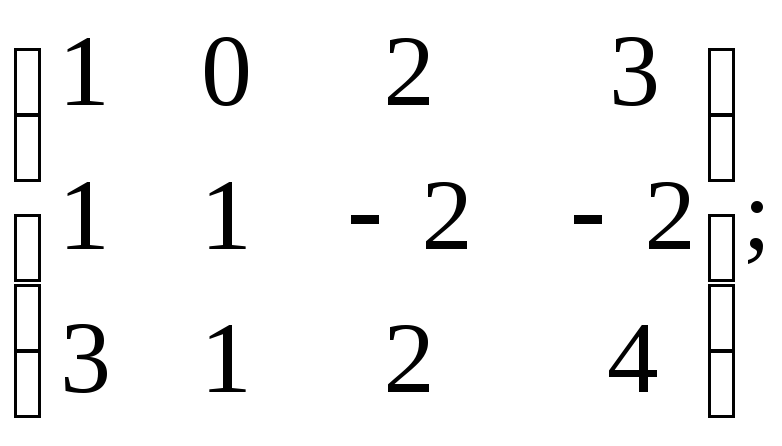 н)
н)
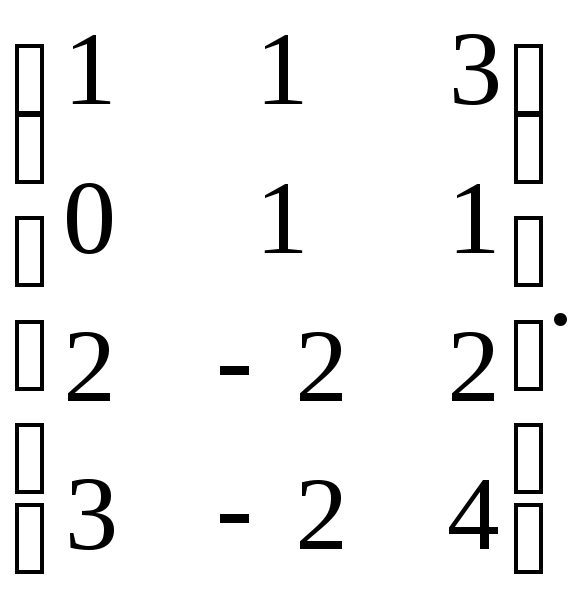
2.7. Покажите что, приписывание к матрице одной строки или одного столбца или не меняет её ранга, или увеличивает его на 1.
2.8. Вычислить ранг матрицы
 методом окаймляющих миноров.
методом окаймляющих миноров.
2.9. Найти ранги матриц, приведением к ступенчатому виду:
1)
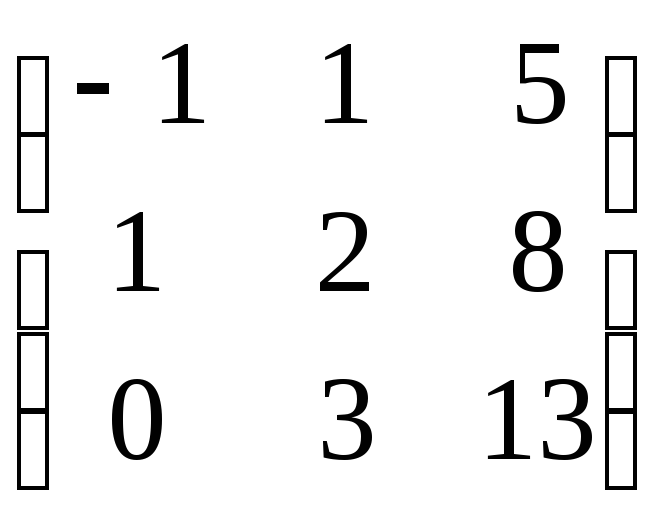 .
2)
.
2)
 3)
3)
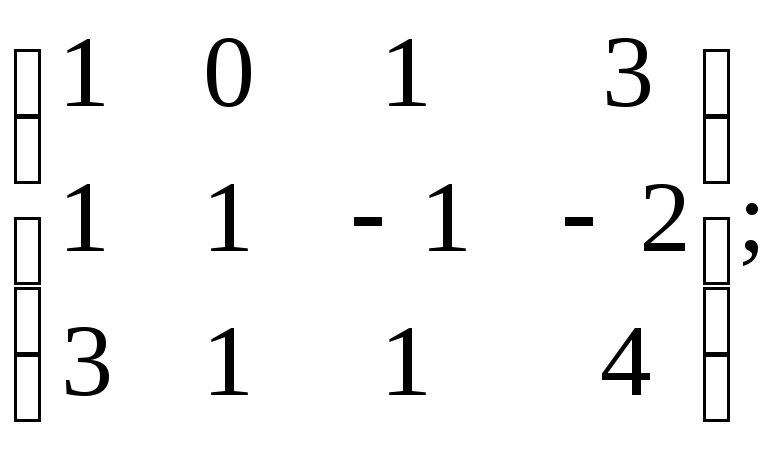
4)
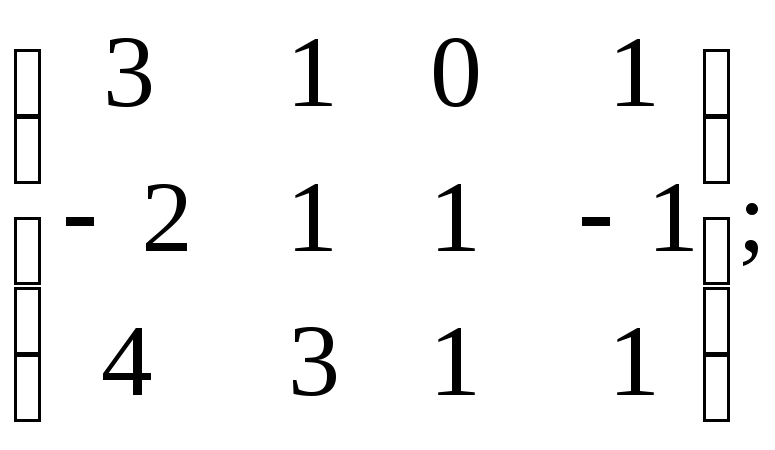 5)
5)

6)
 7)
7)

8)
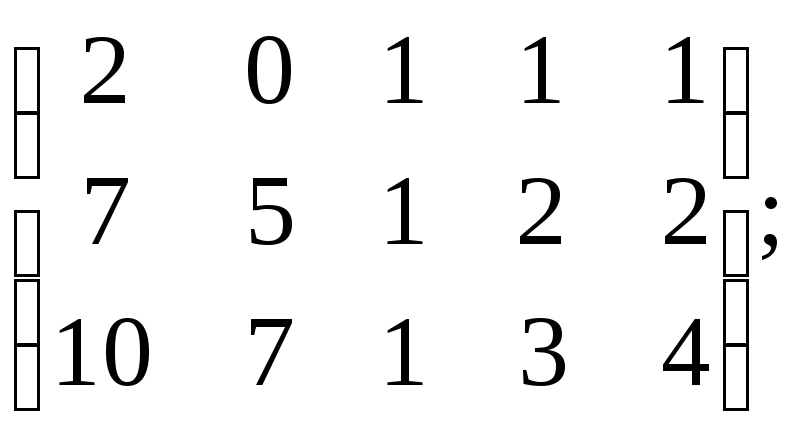 9)
9)

10)
 11)
11)
 ;
;
12)
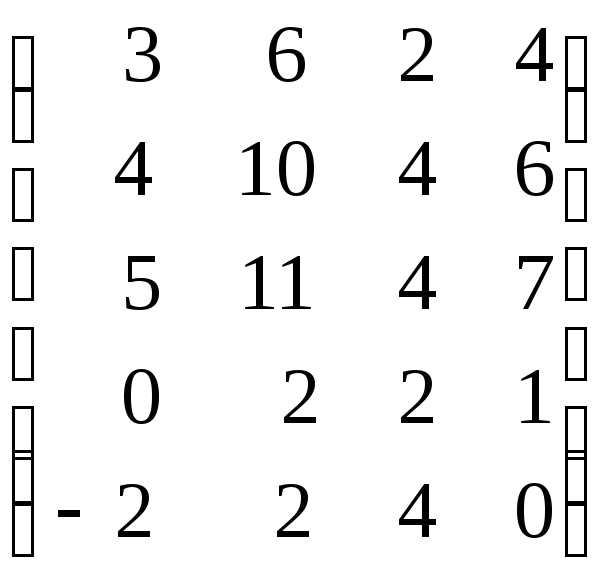 ;
13)
;
13)
 ;
;
14)
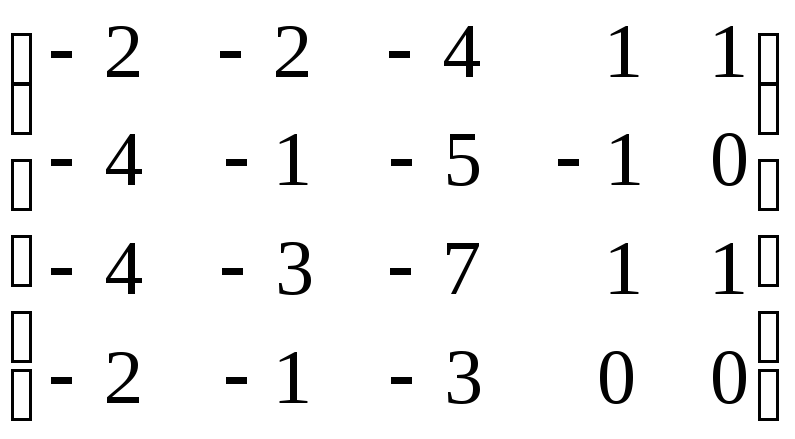 ;
15)
;
15)
 .
.
2.10. Найти числа![]() и
и![]() ,
такие, что
,
такие, что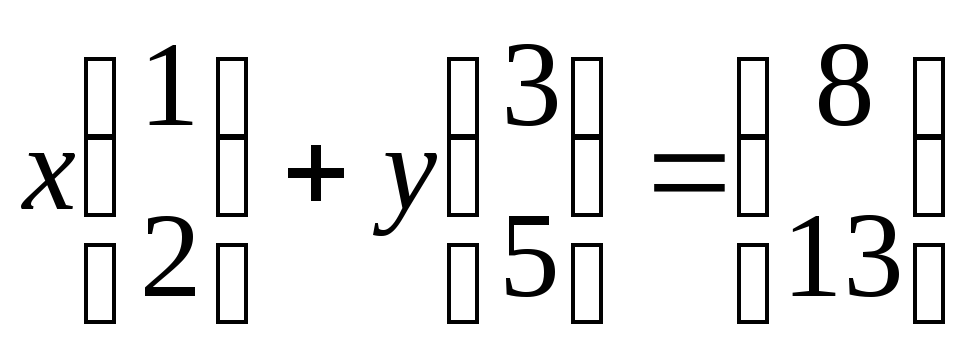 .
.
2.11.Определить, являются ли данные векторы линейно независимыми:
а)
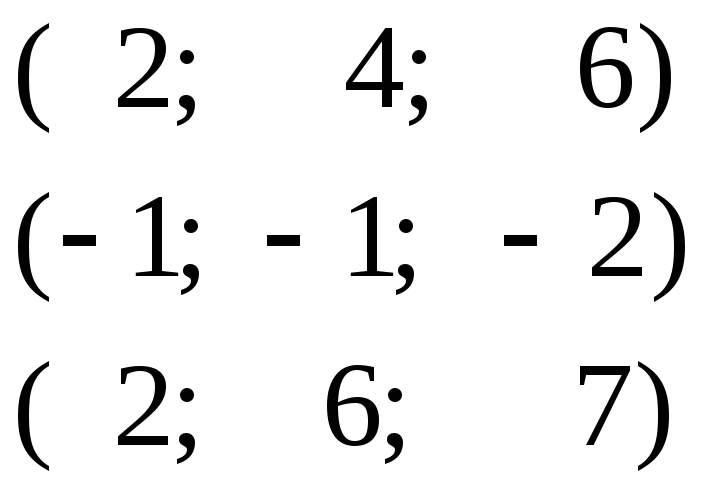 б)
б)
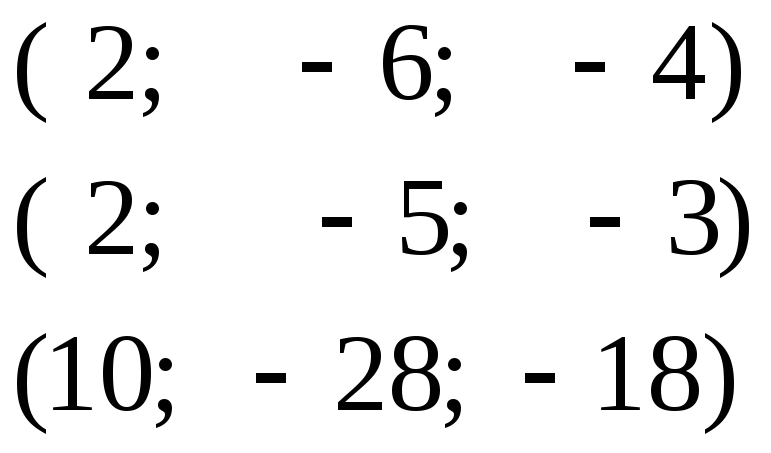
в)
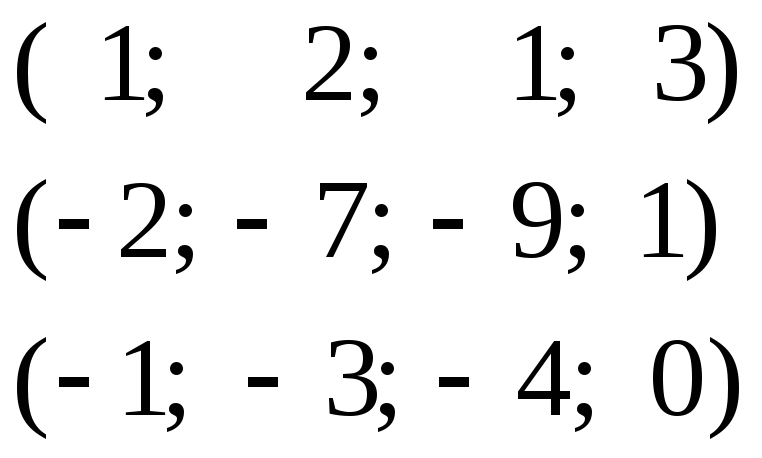 г)
г)
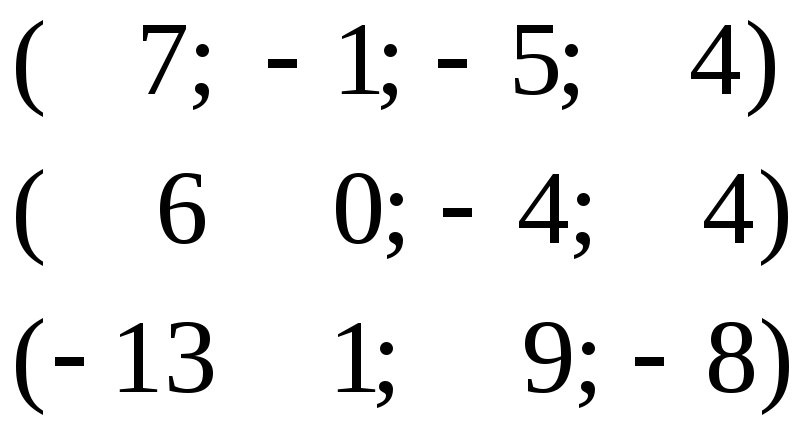
д)
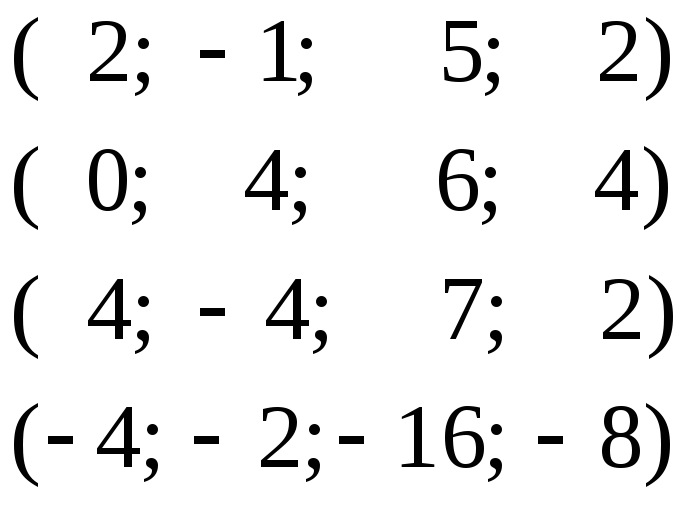 е)
е)
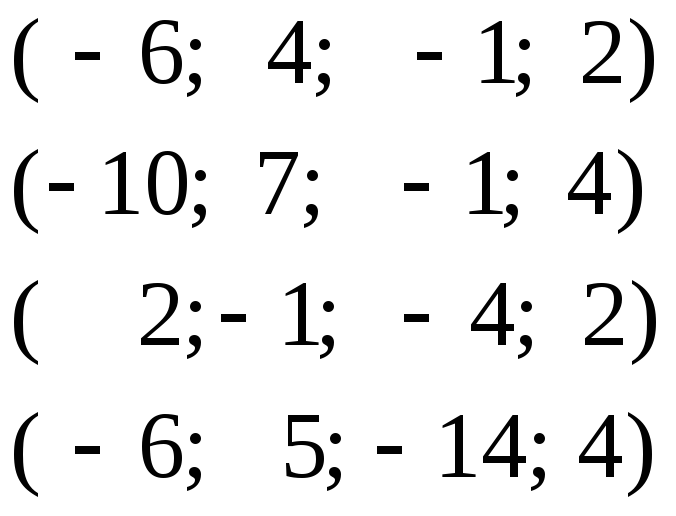
2.12. Найти базу (базис) и ранг системы векторов, представить небазисные векторы в виде линейных комбинаций базисных векторов:
1)
![]() .
.
2)
![]()
![]() .
.
3)
![]()
![]()
![]()
![]()
4)
![]()
![]()
![]()
![]()
5)
![]()
![]()
![]()
6)
![]()
![]()
![]()
7)
![]()
![]()
![]()
8)
![]()
![]()
![]()
![]()
![]()
9)
![]()
![]()
![]()
![]()
![]()
10)
![]()
11)
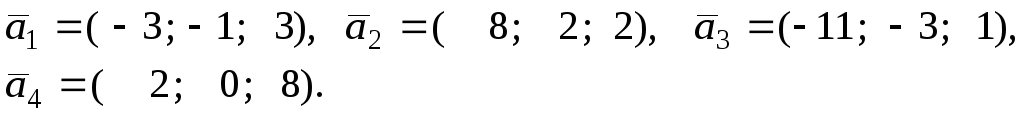
12)
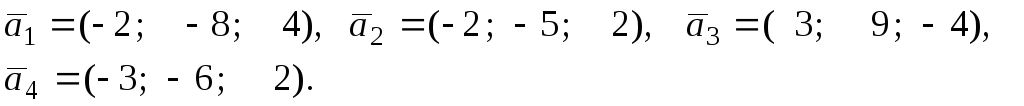
13)
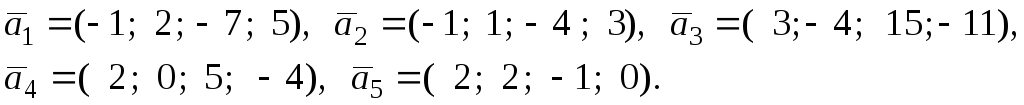
14)

2.13. Привести матрицу к приведённому ступенчатому виду. Найти базис системы строк матрицы. Найти её ранг. Найти базис системы столбцов и выразить небазисные столбцы через базисные.
а)
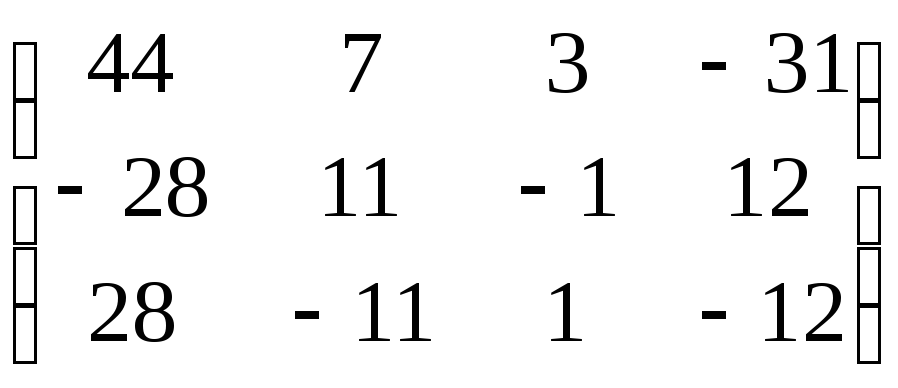 ,
б)
,
б)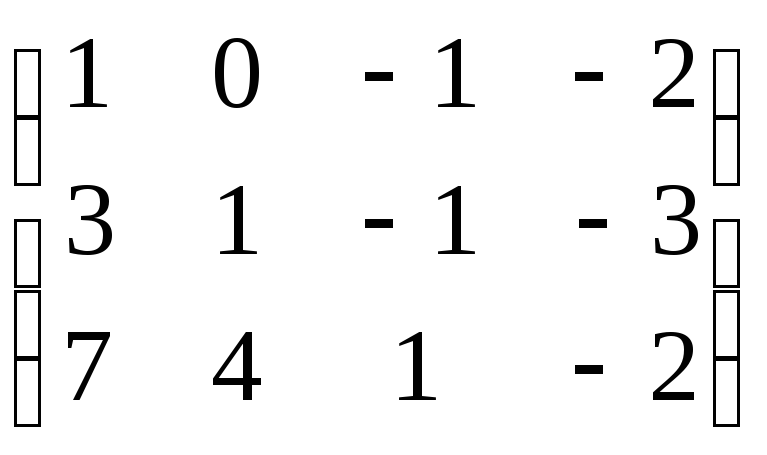 , в)
, в) ,
,
д)
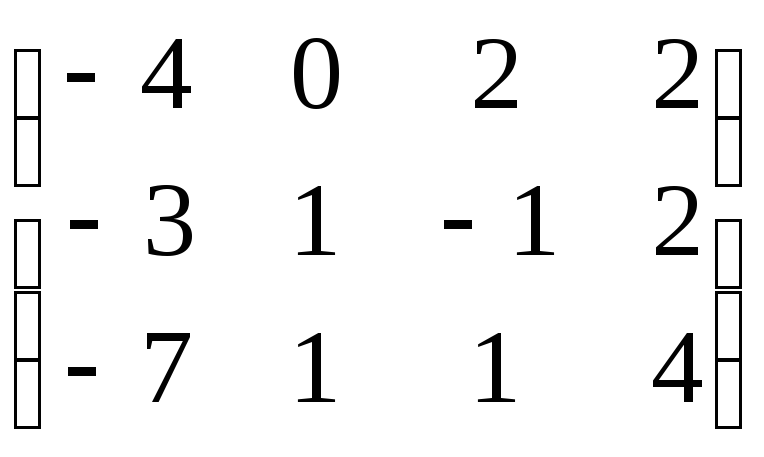 , е)
, е) , ж)
, ж)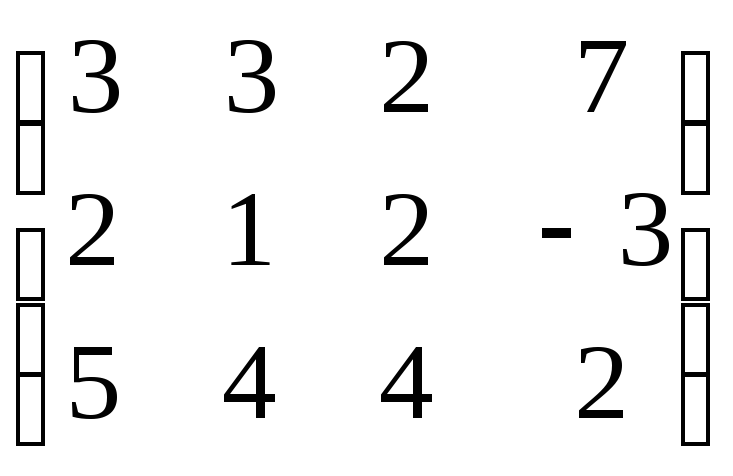 , ж). з)
, ж). з)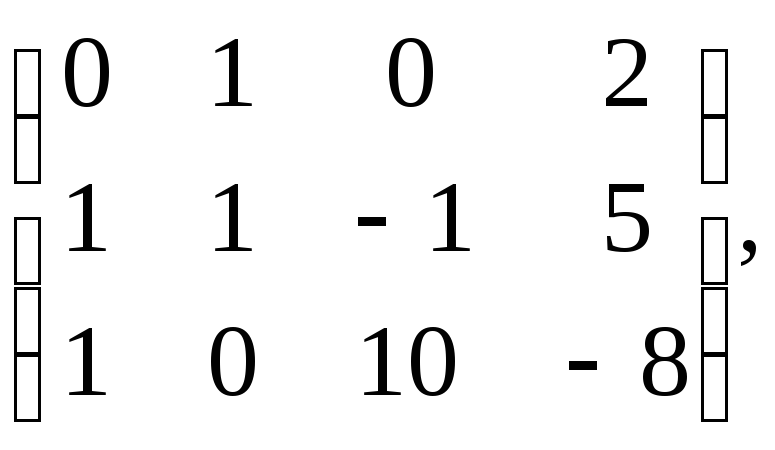 и)
и)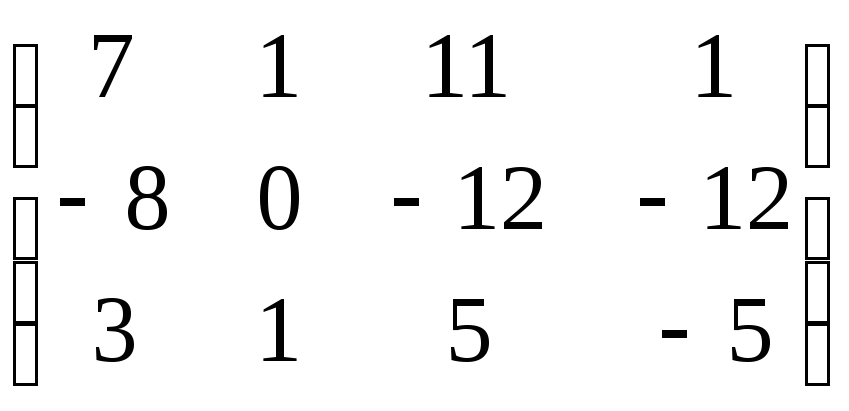 , к)
, к) ,
,
л)
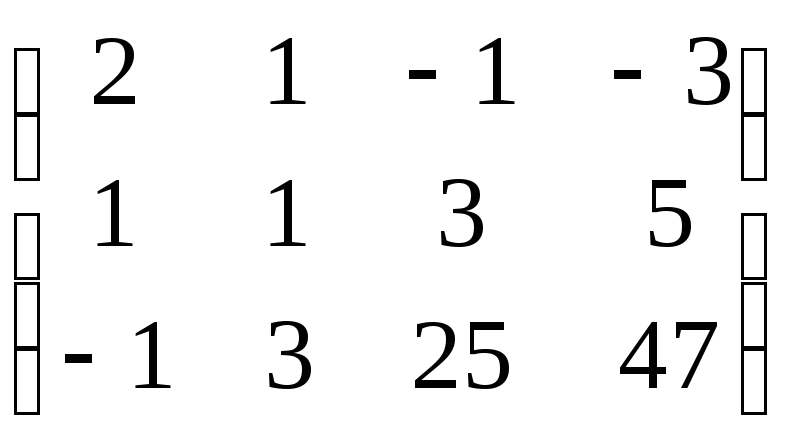 , м)
, м)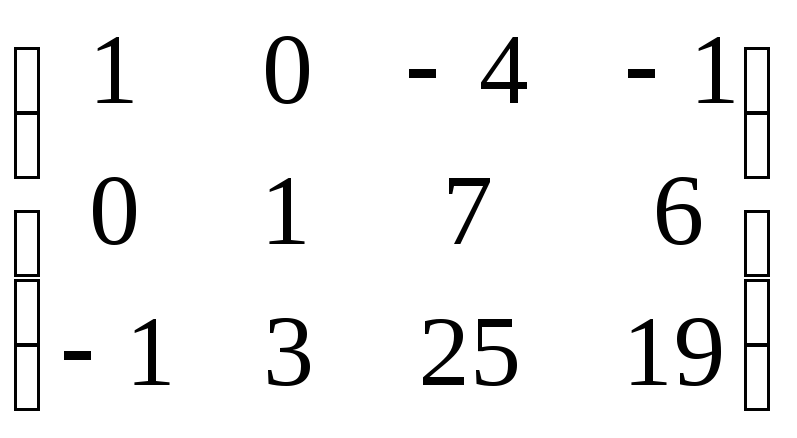 ,
,
2.14. Найти обратную матрицу
![]() по данной матрице
по данной матрице
![]() :
:
1)
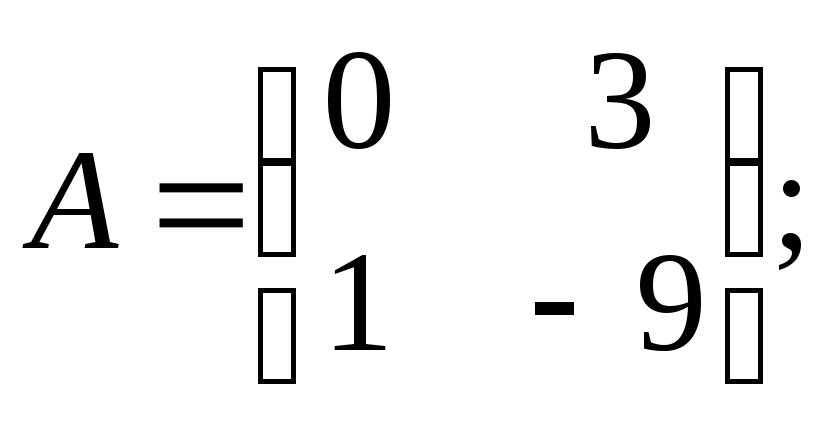 2)
2)
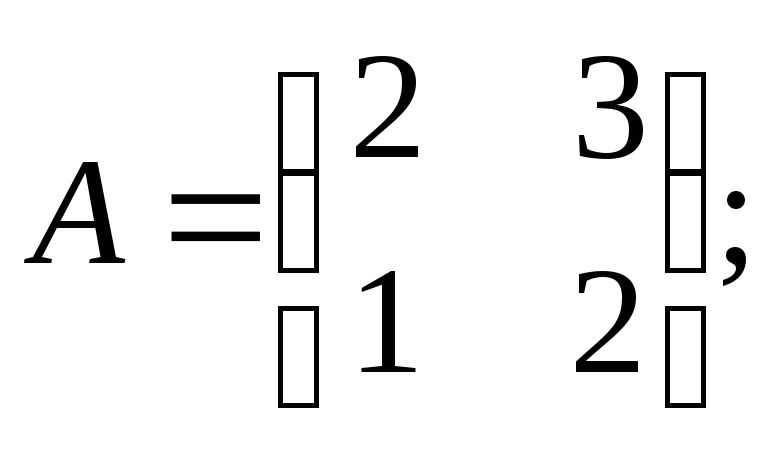 3)
3)
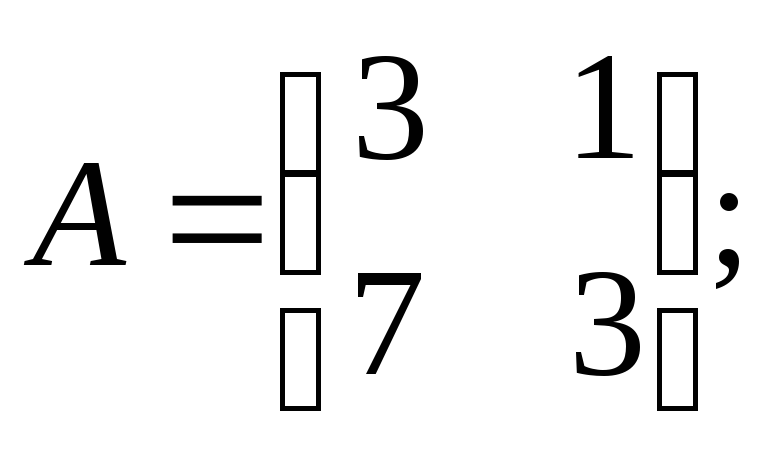 4)
4)
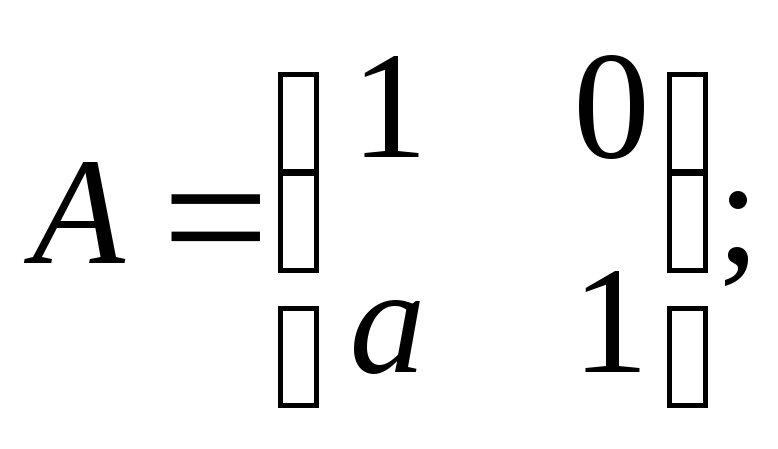
5)

2.15. Вычислить матрицу, обратную к
данной матрице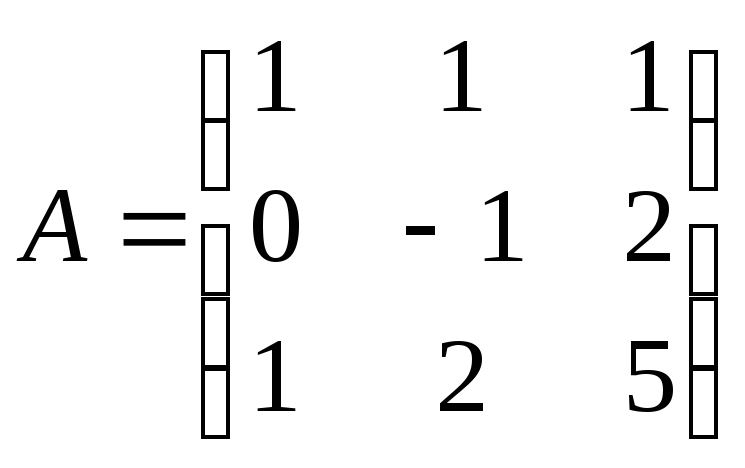 .
.
2.16. Вычислить обратную матрицупо формуле обратной матрицы:
а).
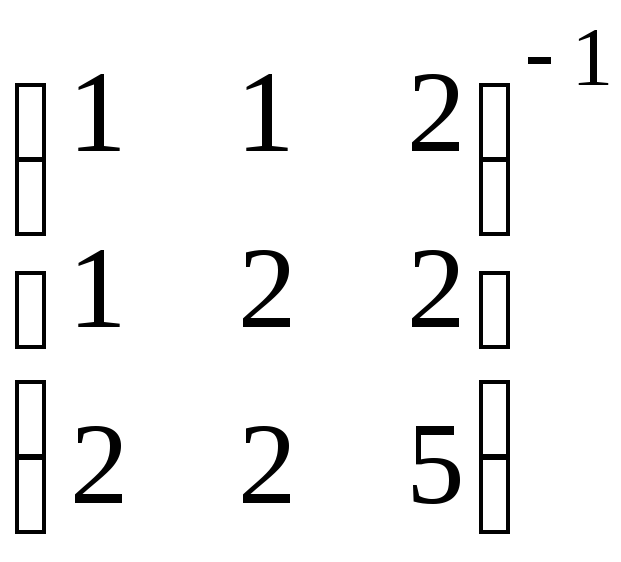 .б).
.б).
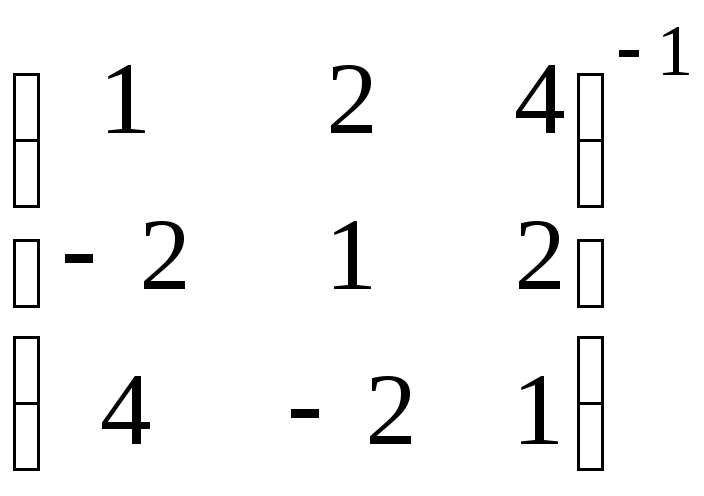 .в).
.в).
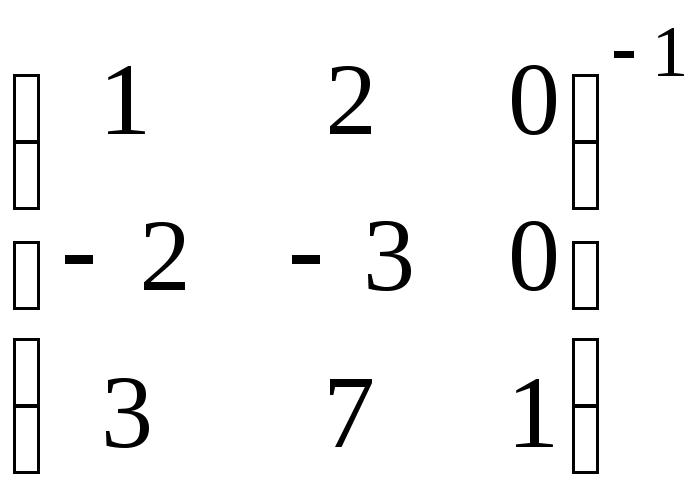 .
.
г).
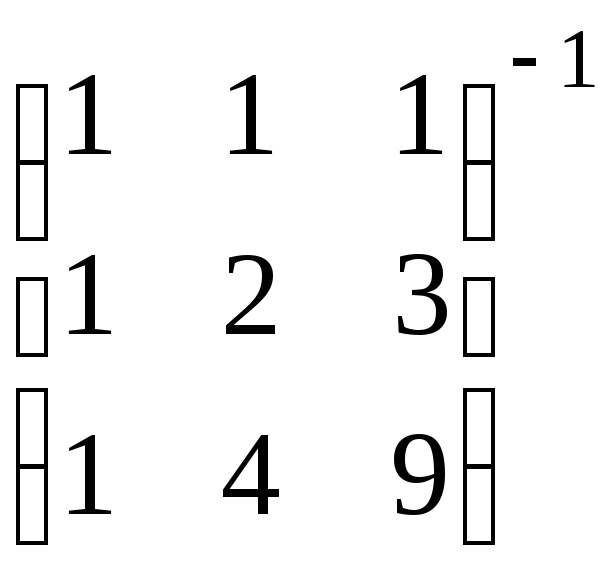 .д).
.д).
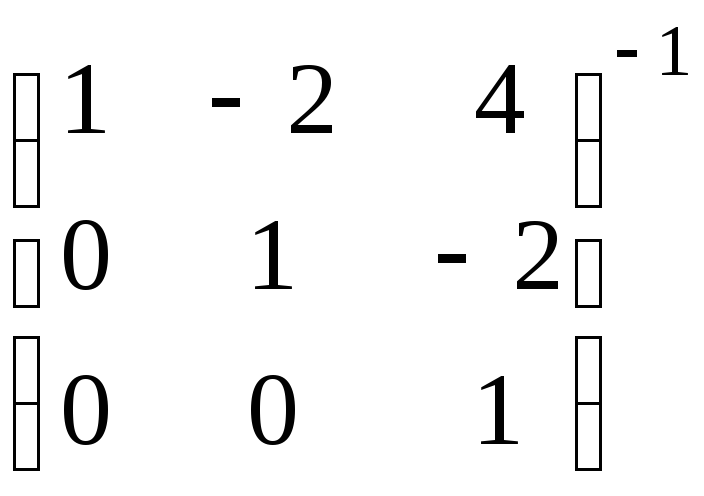 е).
е). 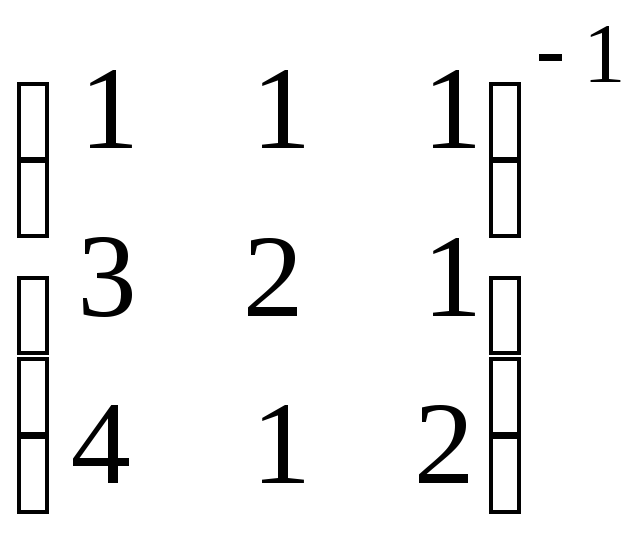 .
.
Вычисление обратной матрицы можно также осуществить с помощью элементарных преобразований строк:
 .
.
2.17. Вычислить обратную матрицу![]() для данной матрицы
для данной матрицы![]() с помощью элементарных преобразований
строк. В конце решения сделать проверку
с помощью элементарных преобразований
строк. В конце решения сделать проверку![]() :
:
а)
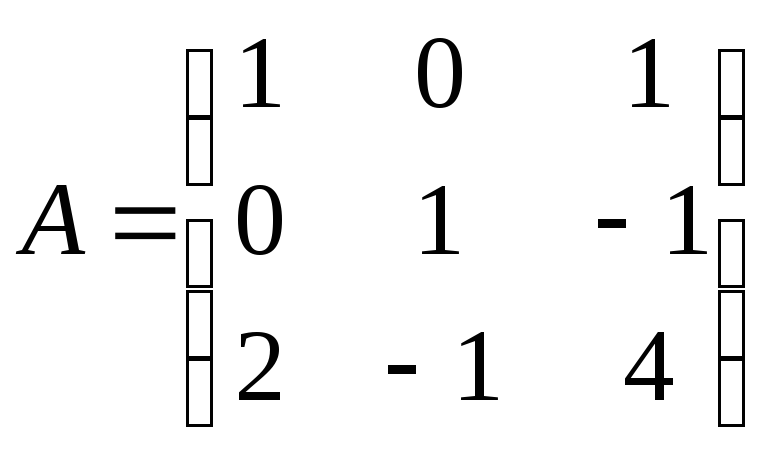 ;
б)
;
б)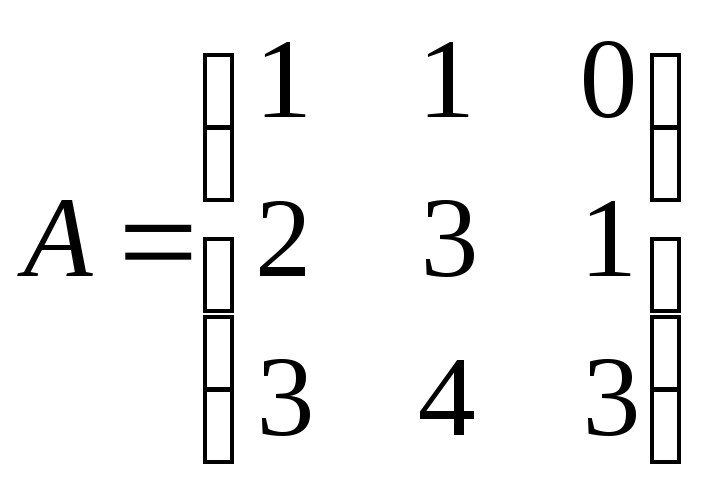 ;
;
в)
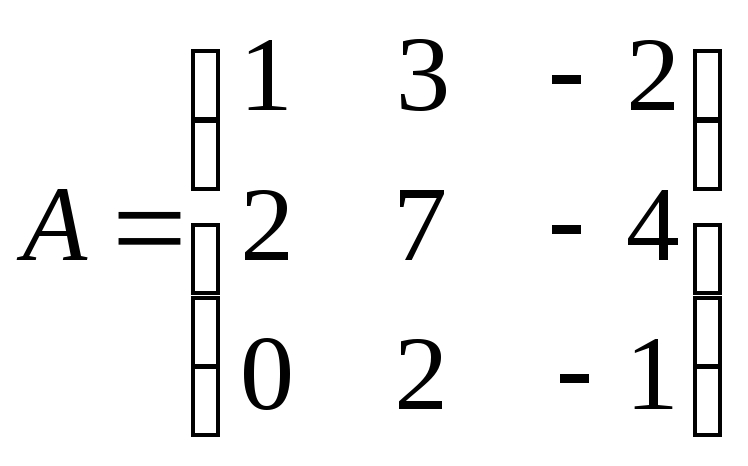 г)
г)![]() =
=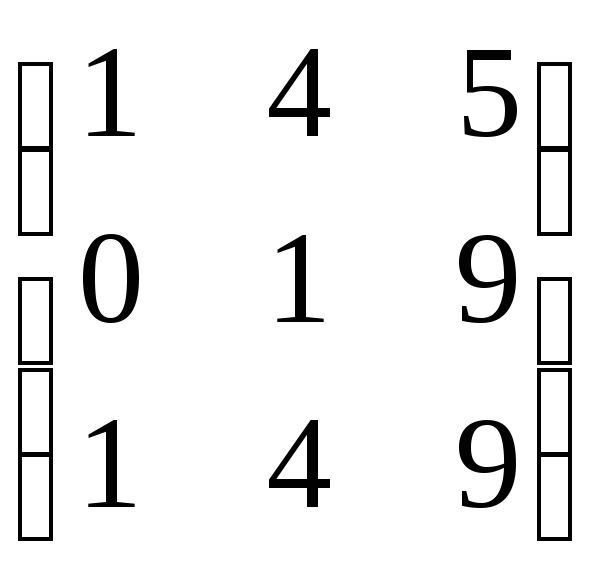 ;
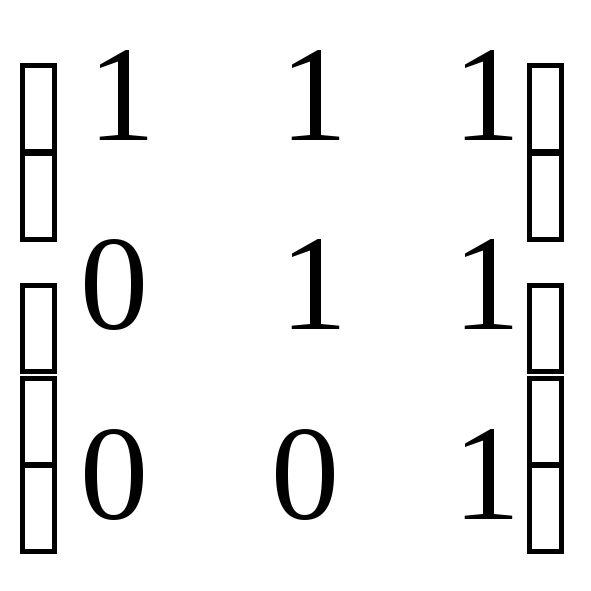
д)
;
д)![]() =
=
2.18. Найти с помощью элементарных преобразований матрицу обратную данной:

2.19.Вычислить матрицу обратную данной.
1.
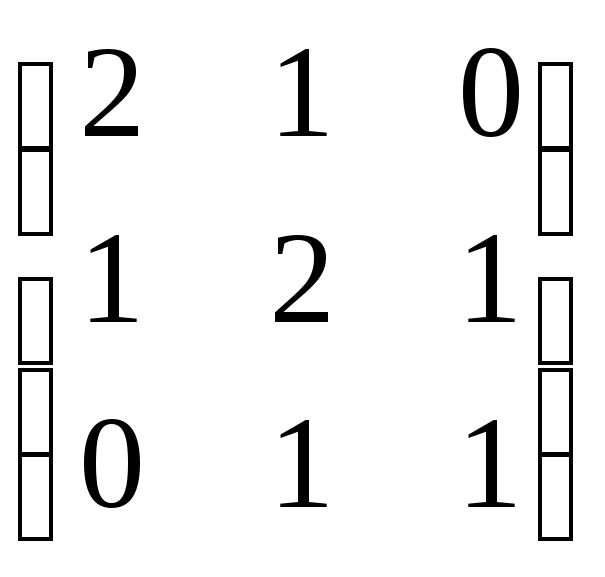 .
2.
.
2. .
3.
.
3.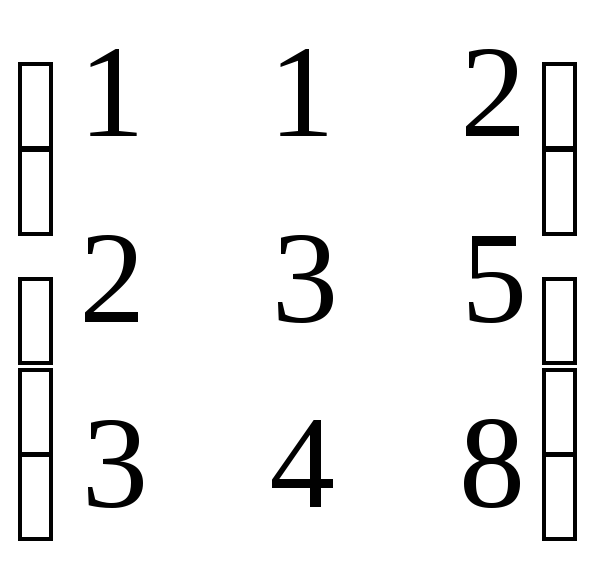 .
.
4.
 .
5.
.
5.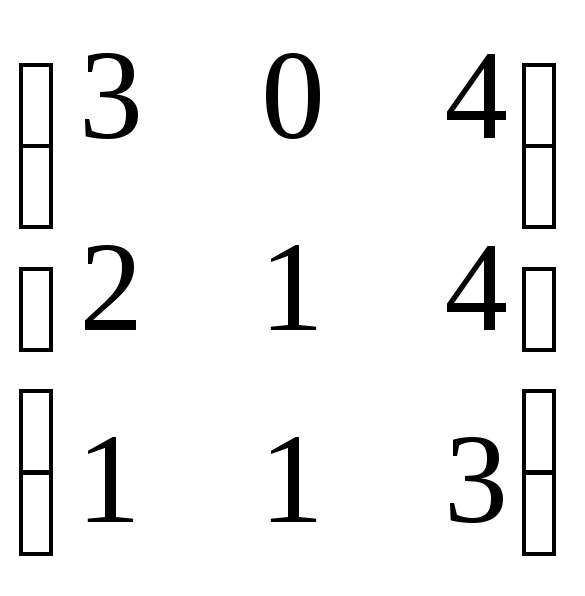 .
6.
.
6.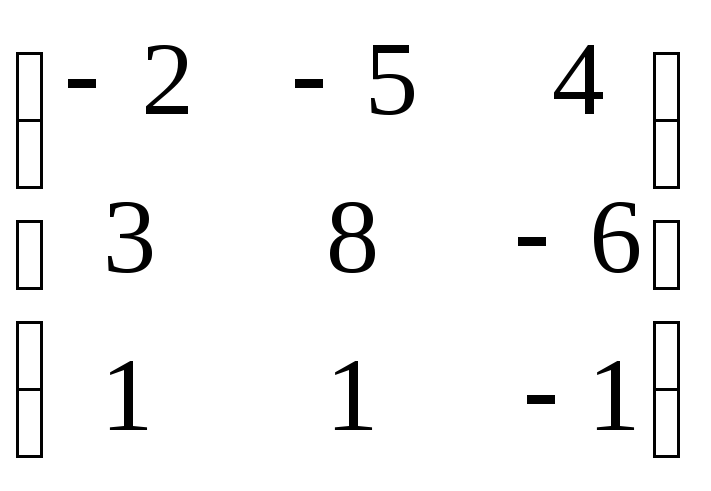 .
.
7.
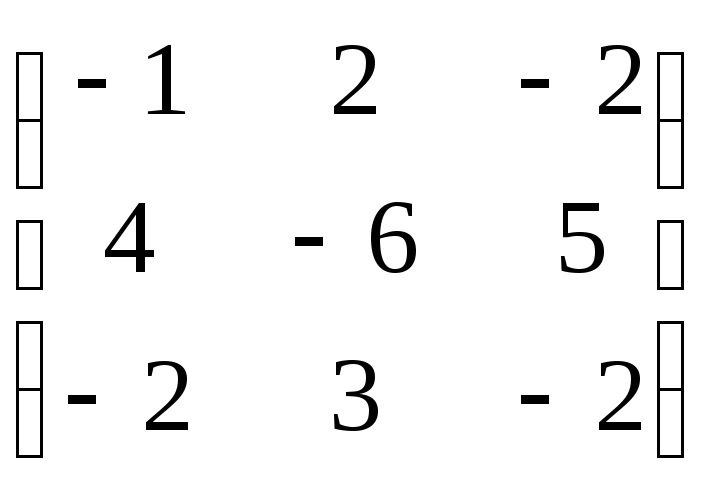 .
8.
.
8.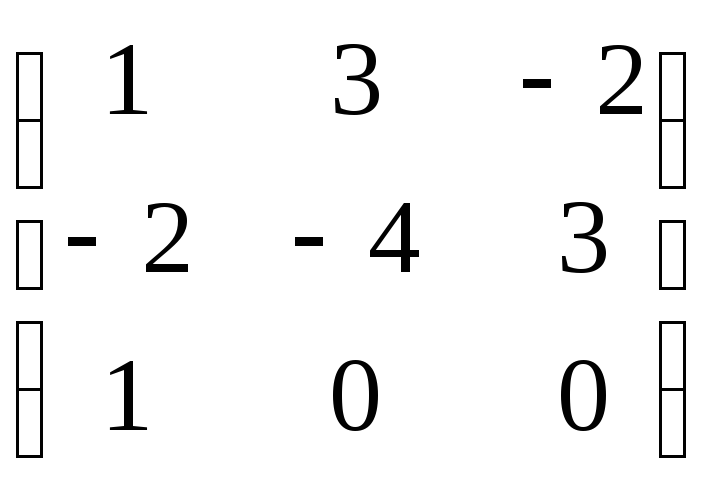 .
9.
.
9.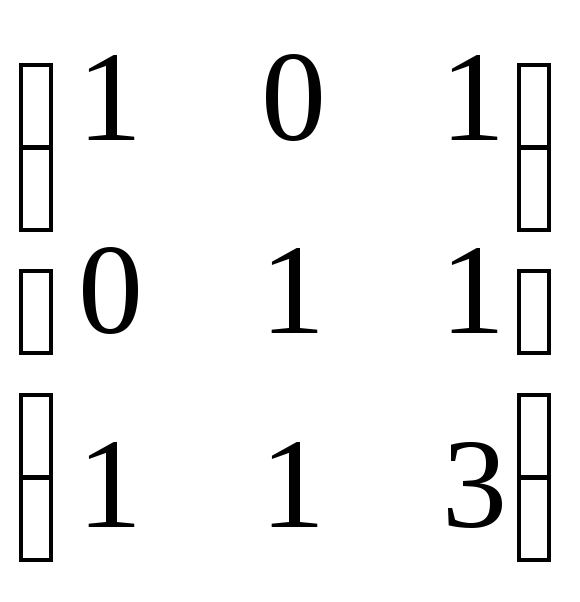 .
.
10.
 .
11.
.
11.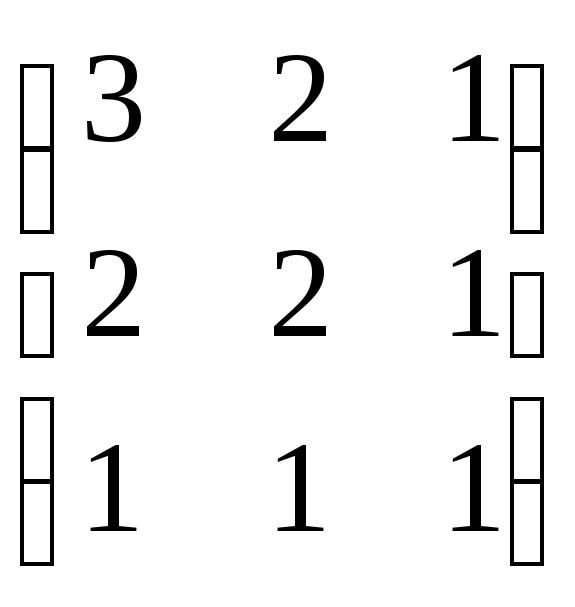 .
12.
.
12.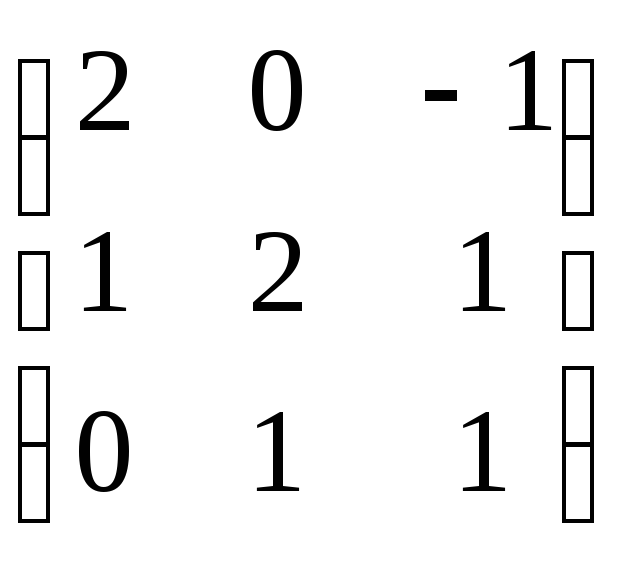 .
.
13.
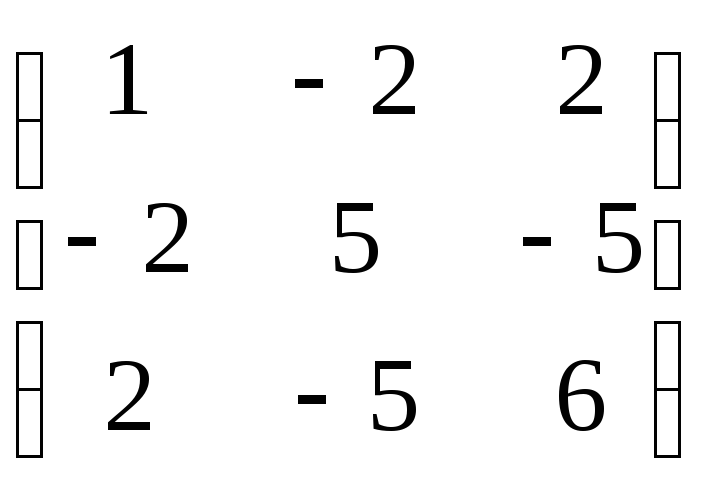 .
14.
.
14.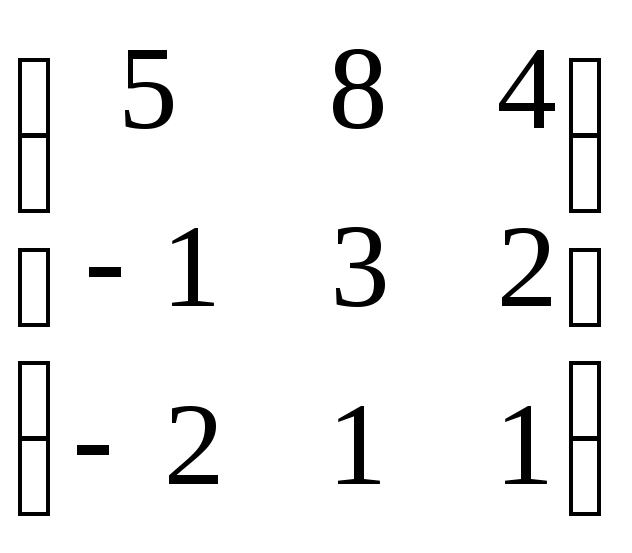 .
15.
.
15.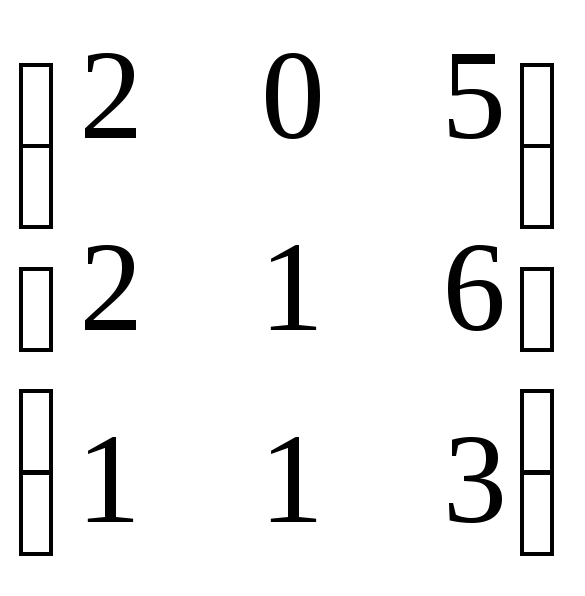 .
.
16.
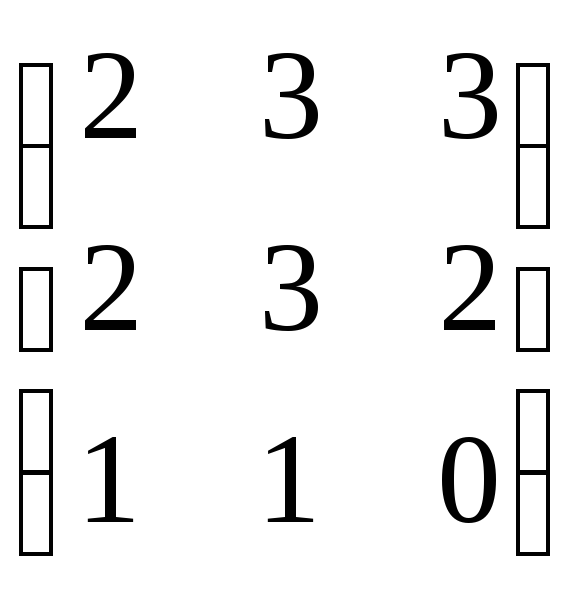 .
17.
.
17.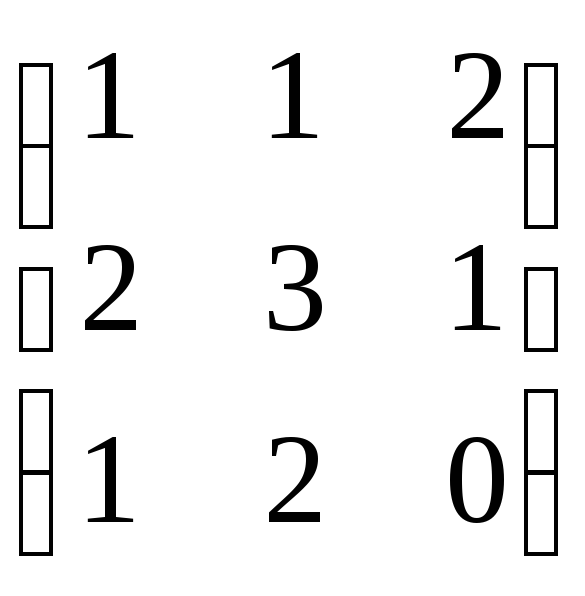 .
18.
.
18.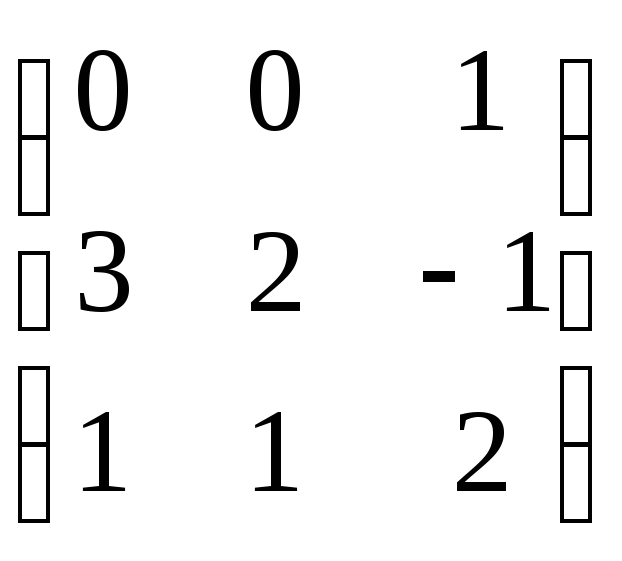 .
.
19.
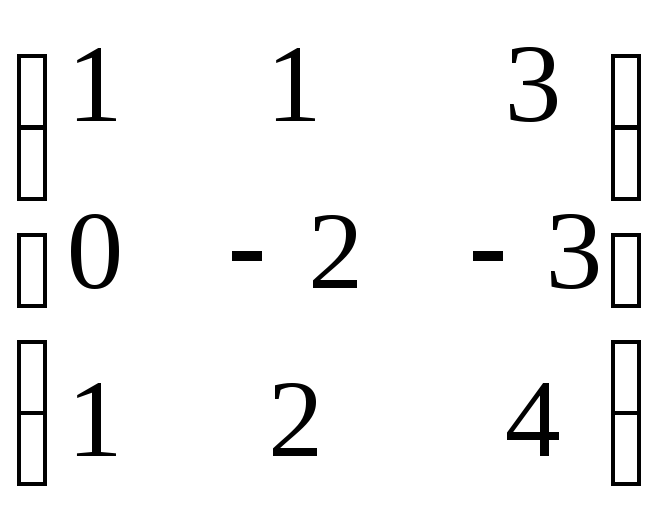 .
20.
.
20.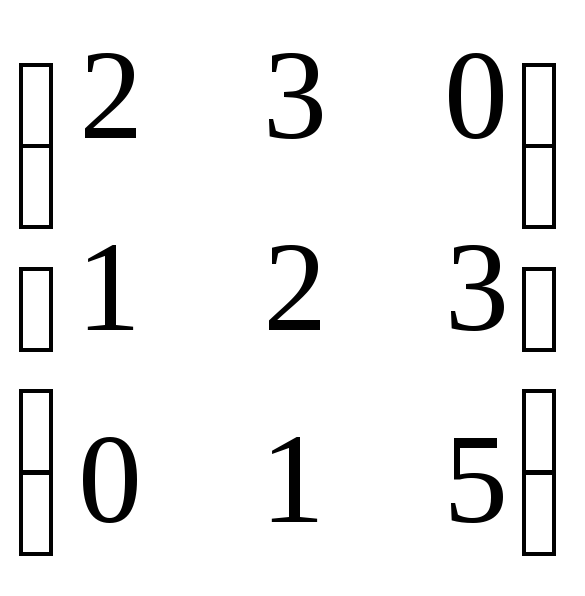 .
21.
.
21.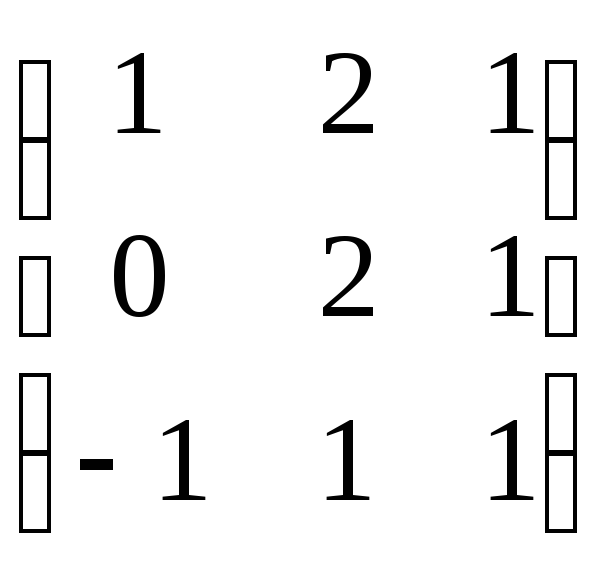 .
.
22.
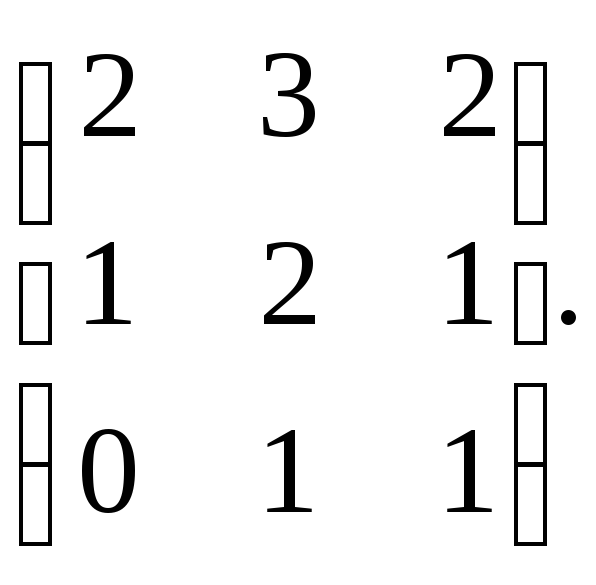 23.
23.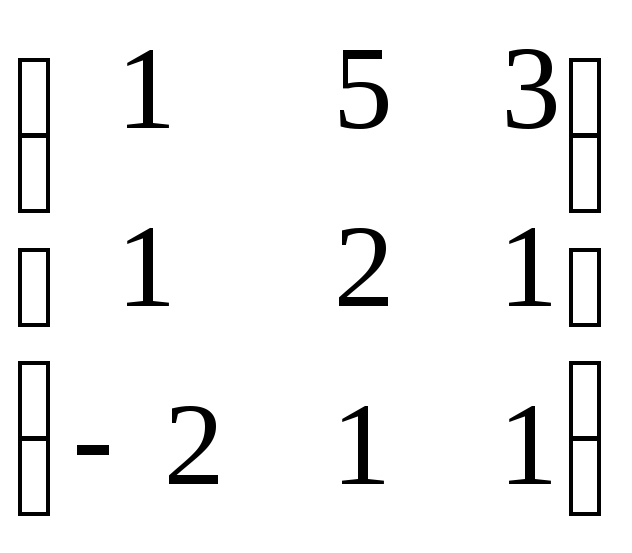 .
24.
.
24.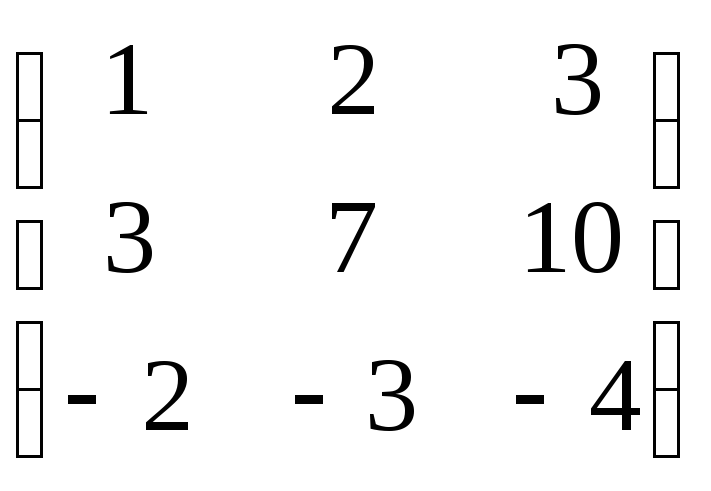 .
.
25.
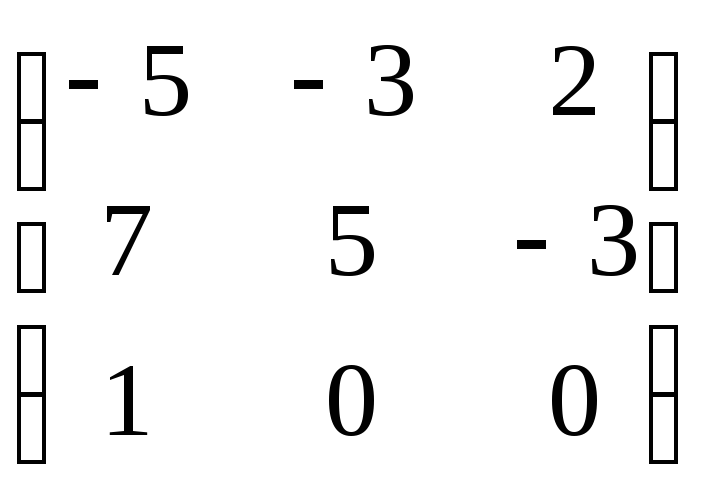 .
26.
.
26.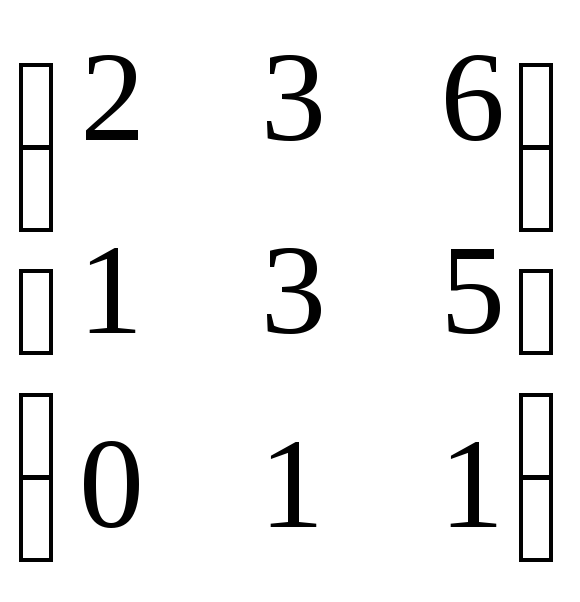 .
27.
.
27.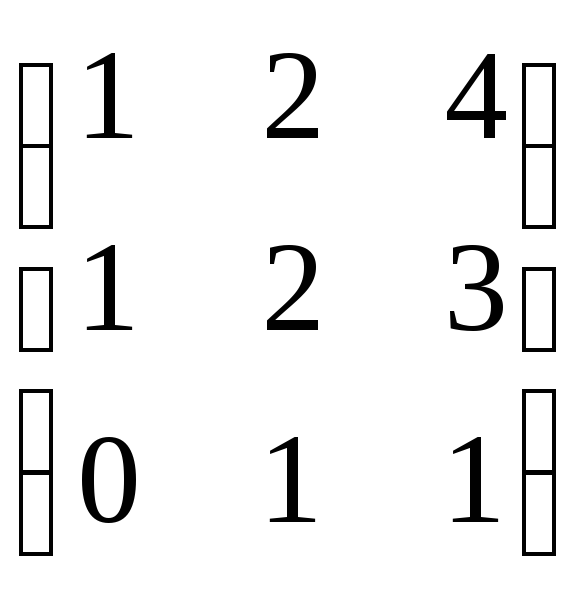 .
.
28.
 .
29.
.
29.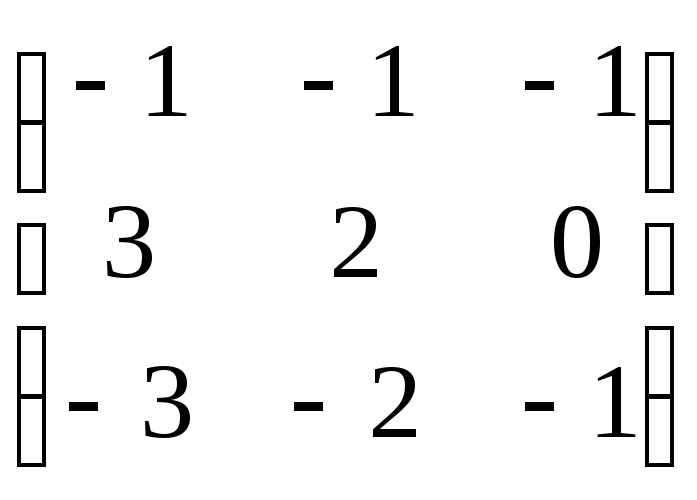 .
.
2.20.С помощью обратной матрицы решить матричные уравнения:
а)
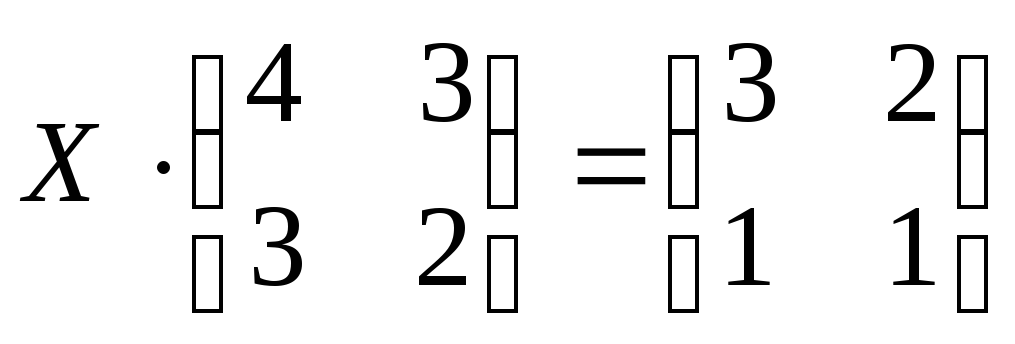 ;
;
б)
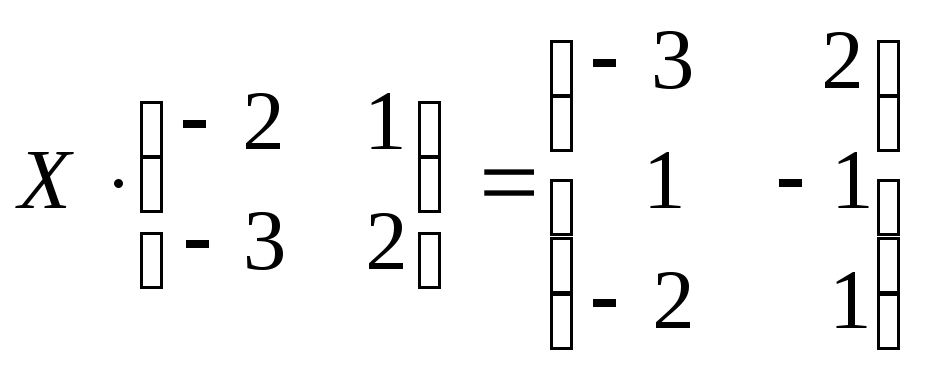 ;
;
в)
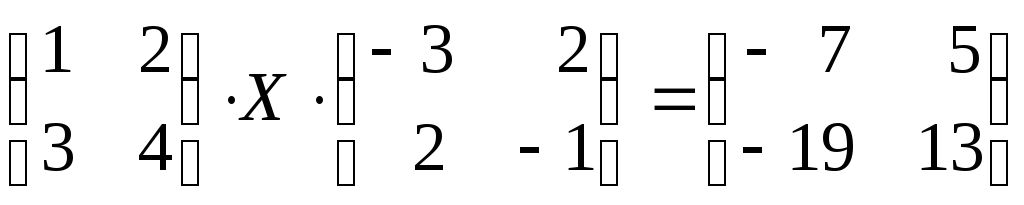
г)
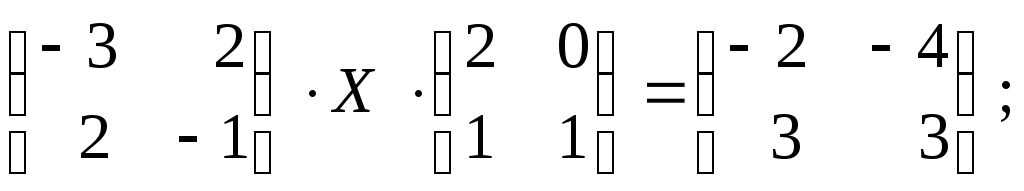
д)
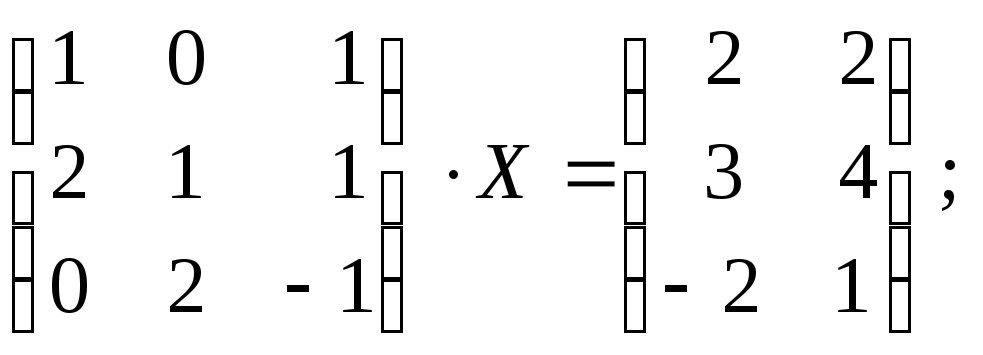
е)
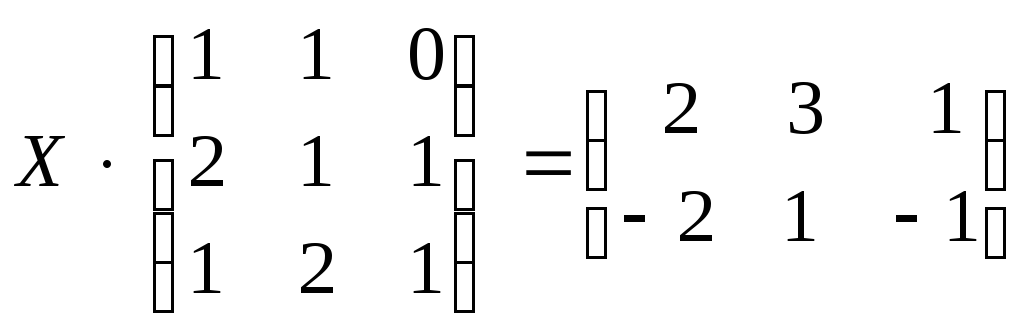 .
.
2.21.Найти общее решение матричного уравнения
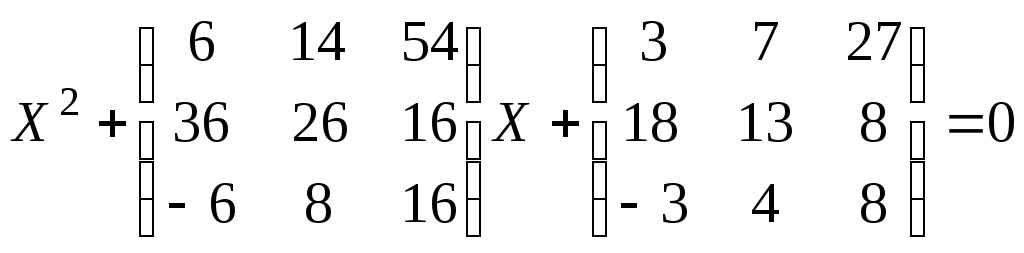 .
.
Ответы на задачи к главе 2
